Модели и характеристики непрерывных измерительных сигналов

При изучении и исследовании измерительных сигналов их рассматривают как функцию времени, характеристики которой содержат информацию, заключенную в сигнале.

Рассмотрим модели и характеристики измерительных сигналов, широко используемых в измерительных приборах и системах [6].

Импульсным называется сигнал, величина которого ничтожно мала в любой точке временной оси, за исключением конечной области.

К характерным импульсным сигналам относятся, сигналы форма и аналитическое описание которых представлено в табл. 3.1.

Информативными характеристиками и параметрами импульсных сигналов являются: форма и уровень сигнала в функции времени x(t); амплитудное (максимальное) значение max x(t); длительность сигнала Т; период повторения; крутизна переднего (dx/dt)_передн или заднего (dx/dt)_задн фронта; площадь под сигналом

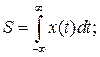(3.1)

энергия сигнала 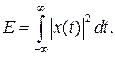(3.2)

Следует отметить, что площадь S для всех рассмотренных сигналов, кроме единичной функции, ограничена и конечна. Для единичного импульса (δ - функция Дирака) и Гаусова сигнала 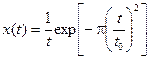площадь сигнала S=1.

Таблица 3.1.

Наименование сигнала	Форма сигнала	Аналитическое описание сигнала
единичная функция отличная от нуля в области 0<t<∞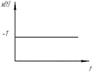
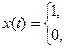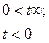
единичный импульс или δ - функция Дирака
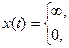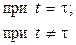
прямоугольный импульс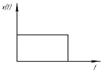
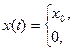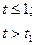
экспоненциальный импульс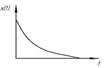

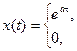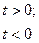
Продолжение таблицы 3.1.

Наименование сигнала	Форма сигнала	Аналитическое описание сигнала
пакет синусоид		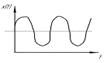x(t)= sin ωt
затухающая синусоида		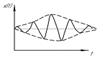x(t)= е-αt sin ωt
Гаусов импульс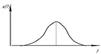
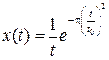
импульс типа		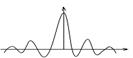x(t)= sin ωt/t
импульс типа		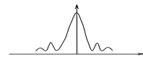x(t)= (sin t/t)2

Энергия E всех рассмотренных сигналов, кроме единичной функции и δ - функция Дирака, конечна, поэтому можно записать

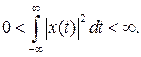(3.3)

Сигналы, значения которых повторяются через постоянные интервалы времени Т, называются периодическими. Для периодических сигналов справедливо соотношение

x(t)= x(t+kT), k=0, ± 1, ± 2, ± 3,… (3.4)

где T – период сигнала.

На рис. 3.3 приведены характерные периодические сигналы.

Если известно поведение периодического сигнала за время T, то полностью известно его прошлое и будущее. Поэтому такой сигнал несет мало информации. Однако его изучение реакции на него позволяет получить различные характеристики измерительного устройства (АЧХ и ФЧХ, параметры запаздывания и искажения и т. п.).

Периодический сигнал используется в качестве несущего сигнала, промодулированного полезным сигналом или помехой с целью последующего их разделения по спектру и выделения или подавления.

Синусоидальный сигнал x(t)=x_m(sinωt+φ) определяется тремя параметрами: амплитудой x_m, частотой ω и фазой φ. Любой из этих параметров при осуществлении амплитудной, частотной или фазовой модуляции может быть информативным (т. е. нести информацию о контролируемом процессе).

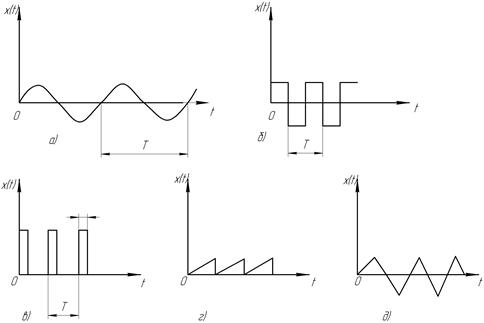
Рис.3.3. Периодические измерительные сигналы

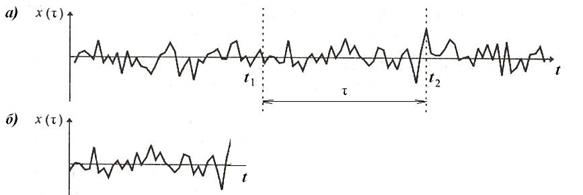
Рис.3.4. Случайные сигналы: а – ансамбль реализации;

б – отдельный фрагмент случайного процесса

(выборная реализация на интервале τ)

Любой периодический сигнал может быть представлен (математически описан) рядом Фурье 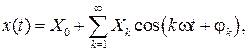при этом параметры Х₀, Х_k, φ_k могут быть информативными. Например, при исследовании вибраций объектов, приборов и устройств периодические сигналы являются полезными информативными сигналами.

Для периодических сигналов для определения площади под сигналом S₀ энергии сигнала E вместо интегралов (3.1) и (3.2) можно рассматривать среднее значение за период T

или 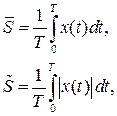(3.5)

или среднюю мощность

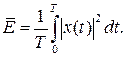(3.6)

Сигнал, состоящий из конечного числа периодических составляющих, не имеющих кратного периода, называется почти периодическим, например

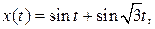(3.7)

для которого невозможно удовлетворить условию периодичности (3.4). Если взять приближенное значение 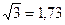, то получим "период" сигнала вида (3.7) T=200π. При более точном значении T=1,7318 "период" T=20000π.

Важный класс составляют случайные сигналы, создаваемые случайными процессами в объектах и системах, о которых имеются неполные сведения.

Случайные сигналы могут быть созданы посредством специальных генераторов.

Характеристики случайных сигналов известны только с определенной вероятностью. Случайный сигнал x(t) полностью характеризуется только бесконечным множеством реализаций, образующих ансамбль (рис. 3.4, а). Взятый из этого ансамбля отдельный сигнал x₁(t) (рис. 3.4, б) называется реализацией или выборочной функцией случайного сигнала x(t).

Исчерпывающей характеристикой случайного сигнала является функция распределения вероятностей F(x). Для ее определения рассматривается сечение всех реализаций ансамбля x(t) в момент времени t₁ и находится вероятность того, что x < x₁, т.е.

F(x)=P[x < x₁ ]. (3.8)

Функция распределения F(x) называется интегральным законом распределения. Она существует для всех случайных величин, непрерывных и дискретных, и полностью характеризует случайную величину x.

Для непрерывных случайных процессов наряду с функцией распределения вводится понятие плотности распределения (дифференциальный закон распределения)

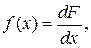(3.9)

причем

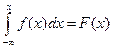и 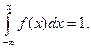(3.10)

Случайные процессы могут быть стационарными, характеристики которого не изменяются во времени на интервале наблюдения, и нестационарными.

На практике обычно имеют дело со стационарными и, в частности, с эргодическими случайными процессами, для которых усреднение по ансамблю совпадает с усреднением во времени. При этом для получения усредненных характеристик во времени нужна лишь одна реализация.

Поскольку интегральный F(x) и дифференциальный f(x) законы распределения не всегда известны, то вместо них вводят совокупность неслучайных характеристик, так называемых моментов. Совокупность всех моментов M_i (i=1,2,…) является полной характеристикой закона распределения. На практике ограничиваются первыми двумя или четырьмя моментами.

Первым моментом или средним значением случайной величины x(t) называется величина

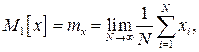(3.11)

где N – число дискретных значений x_i.

Для стационарного эргодического процесса

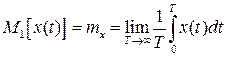(3.12)

и значение m_x характеризует постоянную составляющую случайного сигнала x(t) и называется математическим ожиданием случайного сигнала x(t).

Если известна плотность распределения f(x), то среднее значение и математическое ожидание случайного сигнала можно определить по формулам

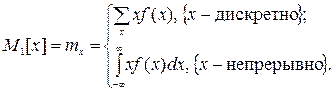(3.13)

Вторым моментом случайного сигнала x(t) называется величина определяемая выражением

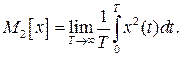(3.14)

Корень квадратный из этого выражения характеризует среднеквадратическое значение сигнала x(t).

Для характеристики рассеяния (отклонения) сигнала x(t) по отношению к его среднему значению (математическому ожиданию) m_x вводят понятие дисперсии

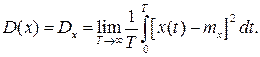(3.15)

Второй момент m_x и дисперсия D_x находятся также по формулам

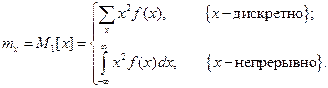(3.16)

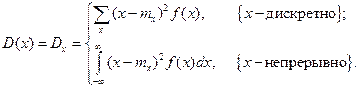(3.17)

Для учета статистических связей между двумя значениями случайного сигнала x(t) и x(t+τ) применяют понятие автокорреляционной функции

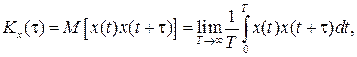(3.18)

равной усредненному значению произведения сигнала в двух точках, сдвинутых на интервал корреляции τ.

Если положить τ=0, то

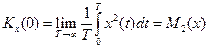, (3.19)

т.е. автокорреляционная функция при τ=0 равна квадрату среднего значения сигнала и достигает при этом своего максимального значения. При τ→∞ K_x(∞)=m_x², т.е. корреляционная К_х стремится к квадрату математического ожидания случайной величины.

Для того, чтобы охарактеризовать статистическую связь между двумя сигналами (например, на входе и выходе прибора) x(t) и y(t), вводится понятие взаимной корреляционной функции:

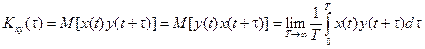. (3.20)

Заметим, что если K_xy(τ)=0, то сигнал x(t) и y(t) статистически независимы, т. е. некоррелированы.

Абсолютное значение взаимной корреляционной функции K_xy(τ) удовлетворяет условию

|K_xy(τ)|² ≤ K_x(0) K_y(0). (3.21)

Взаимная корреляционная функция используется при определении времени задержки в системах, при определении сигналов на фоне шума, при нахождении параметров движения объектов и т. п.

Таким образом, основными характеристиками случайных процессов являются: функция распределения F(x), плотность распределения f(x), математическое ожидание m_x, дисперсия D_x, второй момент M₂(x), автокорреляционная функция K_x(τ), взаимнокорреляционная функция K_xy(τ). Любая из этих характеристик может быть информативным параметром при исследовании случайных процессов.