Наибольший общий делитель многочленов
Определение. Многочлен d(х) называется общим делителем многочленов f(x) и g(x), если d(х)çf(x) и d(х)çg(x).
Определение. Общий делитель многочленов f(x) и g(x) называется их наибольшим общим делителем (НОД), если он делится на любой другой их общий делитель.
Обозначается d(x)=(f(x),g(x)).
Замечания. 1. Если d(х)çf(x) и d(х)çg(x), то, очевидно, сd(х)çf(x) и сd(х)çg(x). Если d(x)=(f(x),g(x)) то и сd(x)=(f(x),g(x)), поэтому принято определять наибольший общий делитель многочленов с точностью до множителя – многочлена нулевой степени.
2. Так как множество многочленов, заданных над областью целостности, само образует область целостности, то (f(x),g(x)) =(g(x), f(x)).
Определение. Многочлены f(x) и g(x) называются взаимно простыми, если их наибольший общий делитель равен 1.
Лемма 1. Если g(x) çf(x), то (f(x),g(x))=g(x).
Доказать самостоятельно.
Лемма 2. Если f(x)= g (x)q(x) +r(x), то (f(x),g(x))=(g (x) ,r(x)).
Действительно, рассмотрим множество всех общих делителей многочленов f(x) и g(x): М={d(х)ôd(x)çf(x)Ùd(x)çg(x)}. И множество всех общих делителей многочленов g (x) и r(x) :K={x(х)ô x(x)çr(x)Ùx(x)çg(x)}. Достаточно доказать, что эти множества совпадают.
1. Пусть d(х)ÎМ Û d(x)çf(x) Ù d(x)çg(x) Þ d(x)çf(x) Ù d(x)çg(x)q(x) Þ
d(x)ç(f(x)-g(x)q(x)) Ù d(x)çg(x) Ûd(x)ç r(x) Ù d(x)çg(x) Þ МÌК.
2. Пусть x(х) Î KÛx(x)çr(x)Ùx(x)çg(x) Þx(x)çr(x)Ùx(x)çg(x)q(x) Þ
x(x)ç(g(x)q(x) + r(x))Ùx(x)çg(x) Ûx(x)çf(x) Ùx(x)çg(x) Ûx(х)ÎМÞ КÌМÞ К=М.
Лемма доказана.
Для нахождения наибольшего общего делителя многочленов будем применять алгоритм Евклида. Пусть нужно вычислить (f(x),g(x)), deg f(x)=n, deg g(x)=s. Не ограничивая общности рассуждений, можем считать, что n>s. По теореме о делении с остатком имеем
f(x)= g (x)q0(x) +r1(x), где r1(x)=0 или deg r1(x)<s;
далее делят делитель на остаток и т. д., в результате получается цепочка равенств
f(x)= g (x)q0(x) +r1(x), где r1(x)=0 или deg r1(x)<s,
g (x)= r1(x)q1(x) +r2(x), где r2(x)=0 или deg r2(x)<deg r1(x),
r1(x) = r2(x)q2(x) +r3(x), где r3(x)=0 или deg r3(x)<deg r2(x),
……………………………….. (11)
rk-2(x) = rk-1(x)q k-1(x) +rk(x), где rk(x)=0 или deg rk(x)<deg r k-1(x),
rk-1(x) = rk(x)q k(x).
Так как степени остатков образуют строго убывающую последовательность натуральных чисел
deg rk(x)<deg r k-1(x)<…<deg r3(x)<deg r2(x)<deg r1(x)<s,
то данный алгоритм конечен, то есть получим остаток, равный нулю.
Теорема 5. Пусть f(x) и g(x) – многочлены, заданные над полем Р. Наибольший общий делитель этих многочленов есть последний, отличный от нуля остаток в алгоритме Евклида.
Доказательство
Применив алгоритм Евклида к многочленам f(x) и g(x), получим цепочку равенств (11). Рассмотрим последнее равенство rk-1(x) = rk(x)q k(x). Из него по определению делимости следует, что rk(x)çrk-1(x), тогда по лемме 1 имеем
(rk(x),rk-1(x))=rk(x).
Применяя к остальным равенствам алгоритма лемму 2, получим цепочку равенств:
(f(x), g (x))=(g (x),r1(x))=(r1(x),r2(x))=…=(rk-2(x),rk-1(x))=(rk-1(x),rk(x))=rk(x) Û
(f(x), g (x))=rk(x), что и требовалось доказать.
Пример. Найти наибольший общий делитель многочленов f(x)=x4+3x3-x2-4x-3, и g(x)=3x3+10x2+2x-3
Замечание. так как наибольший общий делитель многочленов находится с точностью до множителя – многочлена нулевой степени, то есть с точностью до константы, то при его вычислении допускаются «искажения». В частности, остатки можно умножать на некоторые числа, отличные от нуля, что несущественно при нахождении наибольшего общего делителя, так как он находится с точностью до константы. В процессе решения принято места «искажений» отделять двойной чертой.
Делим f(x) на g(x), предварительно умножив его на 3.
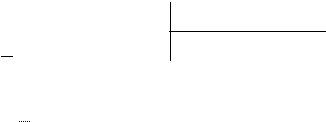 x4+3x3-x2-4x-3 3x3+10x2+2x-3
x4+3x3-x2-4x-3 3x3+10x2+2x-3
3x4+9x3-3x2-12x-9
3x4+10x3+2x2-3x x-1
-x3-5x2-9x-9
-3x3-15x2-27x-27
-3x3-10x2-2x+3
-5x2-25x-30
x2+5x+6
Выполним второе деление.
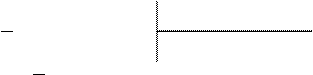 3x3+10x2+2x-3 x2+5x+6
3x3+10x2+2x-3 x2+5x+6
3x3+15x2+18x 3x-5
-5x2-16x-3
-5x2-25x-30
9x+27
x+3
делим еще раз
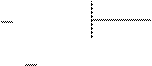 x2+5x+6 x+3
x2+5x+6 x+3
х2+3х х+2
2х+6
2х+6
Итак, последний, отличный от нуля остаток - (х+3), следовательно, (f(x),g(x))=х+3.
Теорема 6(о линейном представлении НОД). Пусть f(x),g(x)ÎP[x], degf(x)=n, deg g(x)=s, (f(x),g(x))=d(x), тогда найдутся такие многочлены u(x) и v(x), что d(x)=u(x)f(x)+v(x)g(x), причем
deg u(x)<deg g(x) и deg v(x)<deg f(x).
Доказательство
Выпишем алгоритм Евклида для многочленов f(x) и g(x):
f(x)= g (x)q0(x) +r1(x),
g (x)= r1(x)q1(x) +r2(x),
r1(x) = r2(x)q2(x) +r3(x),
………………………………..
rk-2(x) = rk-1(x)q k-1(x) +d(x).
Выражая остатки из всех равенств алгоритма поочередно и вводя соответствующие обозначения, получим
r1(x)=f(x)-g (x)q0(x)= u1(x)f(x)+v1(x)g(x);
r2(x)=g(x)-r1(x)q1(x)=g (x)-(u1(x)f(x)+v1(x)g(x)) q1(x) =(-u1(x)q1(x))f(x)+
+(1-u1(x)v1(x) q1(x))g(x) =u2(x)f(x)+v2(x)g(x);
r3(x)= r1(x)-r2(x)q2(x)= (u1(x)f(x)+v1(x)g(x))-(u2(x)f(x)+v2(x)g(x))q2(x)=
=(u1(x)- u2(x)q2(x)) f(x)+(v1(x)- v2(x)q2(x))g(x) = u3(x)f(x)+v3(x)g(x)4
…………………………………………………
d(x)=rk-2(x)-rk-1(x)qk-1(x)=(uk-2(x)f(x)+vk-2(x)g(x))-(uk-1(x)f(x)+vk-1(x)g(x))qk-1(x)
=(uk-2(x)- uk-1(x)q k-1(x)) f(x)+(vk-2(x)- vk-1(x) q k-1(x)) g(x)=uk(x) f(x)+vk(x)g(x)= =u(x)f(x)+v(x)g(x).
Возможность представления доказана. Проверим, как связаны друг с другом степени многочленов, входящие в равенство d(x)=u(x)f(x)+v(x)g(x).
Очевидно, что имеет место только один из четырех взаимно исключающих вариантов:
1° deg u(x)<deg g(x)=s
deg v(x)<deg f(x)=n;
2° deg u(x)<deg g(x)=s
deg v(x)³deg f(x)=n;
3° deg u(x)³deg g(x)=s
deg v(x)<deg f(x)=n;
4° deg u(x)³deg g(x)=s
deg v(x)³deg f(x)=n.
Если выполняется соотношение 1°, то теорема верна. Если верно соотношение 2°, тогда, применяя теорему о делении с остатком, получаем
v(x)=f(x)q1(x)+r1(x), где deg r1(x)<deg f(x)=n, тогда d(x)=u(x)f(x)+v(x)g(x)=
=u(x)f(x)+(f(x)q1(x)+r1(x))g(x)=u(x)f(x)+f(x)g(x)q1(x)+r1(x)g(x).
Если q1(x)=0, то d(x)= u(x)f(x)+r1(x)g(x), где deg u(x)<deg g(x)=s и deg r1(x)<deg f(x)=n, и теорема доказана. Если q1(x)¹0, тогда степень
deg (u(x)f(x)+f(x)g(x)q1(x)+r1(x)g(x))>n+s Û deg d(x)>n+s, что противоречит определению наибольшего общего делителя.
Самостоятельно рассмотреть случаи 3° и 4°.
Следствие. Если (f(x),g(x))=1, то найдутся такие многочлены u(x) и v(x), что u(x)f(x)+v(x)g(x)=1.
Теорема 7. Если h(x)çf(x)g(x) и , (h(x),f(x))=1 то h(x)çg(x).
Доказательство. Действительно, по следствию из теоремы о линейном представлении НОД имеем (h(x),f(x))=1Þ$ u(x), v(x)(u(x)f(x)+v(x)h(x))=1) Þ u(x)f(x) g(x)+v(x)h(x) g(x)=g(x) Получили h(x)çf(x)g(x) Þ h(x)çu(x)f(x)g(x); h(x)çh(x) Þ h(x)çv(x)h(x) g(x) Þ h(x)çu(x)f(x)g(x)+v(x)h(x) g(x) Û h(x)çg(x).
Теорема 8. Если (h(x),f(x))=1 и (h(x),g(x))=1, то (h(x),f(x)g(x))=1.
Доказательство. Пусть, (h(x),f(x)g(x))=d(x), тогда d(x)çh(x) и d(x)çf(x)g(x). Так как d(x)çh(x), а (h(x),f(x))=1, то (d(x),f(x))=1. Но d(x)çf(x)g(x) и (d(x),f(x))=1, следовательно, d(x)çg(x), что противоречит условию (h(x),g(x))=1. Таким образом, наше предположение привело к противоречию, теорема доказана.
Упражнение. Найдите НОД многочленов f(x) и g(x) из кольца 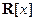 и его линейное представление:
и его линейное представление:
1. 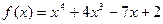 ,
, 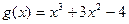 ;
;
2. 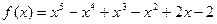 ,
, 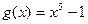 ;
;
3. 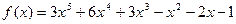 ,
, 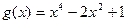 ;
;
4. 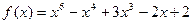 ,
, 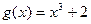 ;
;
5. 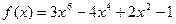 ,
, 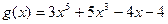 ;
;
6. 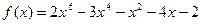 ,
, 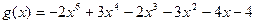 ;
;
7. 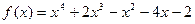 ,
, 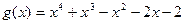 ;
;
8. 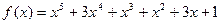 ;
; 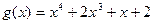 ;
;
9. 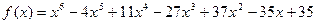 ,
, 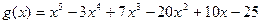 ;
;
10. 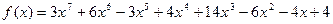 ,
, 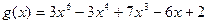 ;
;
11. 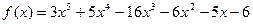 ,
, 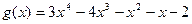 ;
;
12. 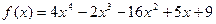 ,
, 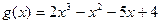 ;
;
13. 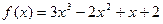 ,
, 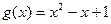 ;
;
14. 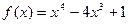 ,
, 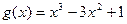 ;
;
15. 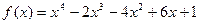 ,
, 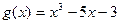 .
.
Дата добавления: 2020-10-25; просмотров: 391;