Исследование устойчивости по корням характеристического уравнения
В разделе 7.1 было показано, что непрерывная система устойчива, если все корни sv(v=1,2,…,n) ее характеристического уравнения лежат в левой полуплоскости (рис.12.1 a). При исследовании импульсных систем вместо s используется новая переменная z=еTs . В теории функций комплексного переменного преобразование, в процессе которого одна переменная заменяется некоторой функцией от новой переменной, а одна область комплексной плоскости отображается в другую, называется конформным преобразованием. Конформное преобразование z=eTs отображает левую полуплоскость плоскости s в область, ограниченную окружностью единичного радиуса на плоскости z (рис. 12.1 б). При этом мнимая ось плоскости s отображается в саму окружность.
Действительно, пусть s1,2 = 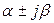 . Тогда
. Тогда
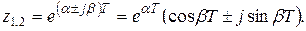
При этом 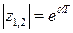 . Для значений
. Для значений 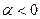 (что соответствует корням s1,2, лежащим в левой полуплоскости плоскости s )
(что соответствует корням s1,2, лежащим в левой полуплоскости плоскости s ) 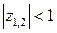 , что соответствует корням z1,2 , лежащим внутри круга единичного радиуса плоскости z. Если
, что соответствует корням z1,2 , лежащим внутри круга единичного радиуса плоскости z. Если 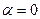 , т.е. если s1,2 располагаются на мнимой оси плоскости s, то корни z1,2 попадают на окружность единичного радиуса плоскости z.
, т.е. если s1,2 располагаются на мнимой оси плоскости s, то корни z1,2 попадают на окружность единичного радиуса плоскости z.
Таким образом, импульсная система устойчива, если все корни ее характеристического уравнения лежат внутри круга единичного радиуса, т.е. если 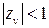 ,
, 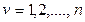 , что совпадает с условием (10.17).Если хотя бы один корень лежит вне круга единичного радиуса, то система неустойчива.
, что совпадает с условием (10.17).Если хотя бы один корень лежит вне круга единичного радиуса, то система неустойчива.
Окружность единичного радиуса представляет собой границу устойчивости для импульсной системы.
Система находится на апериодической границе устойчивости, если в ее характеристическом уравнении
a0zn+a1zn-1+…+an=0 (12.1)
имеется корень zv=1, а остальные корни располагаются внутри круга единичного радиуса (рис.12.1 в). В этом случае переходная составляющая решения разностного уравнения (10.16) с течением времени стремится к значению Cv(zv)i = Cv.
Если в характеристическом уравнении имеется пара комплексных сопряженных корней, расположенных на окружности единичного радиуса (рис.12.1 г), т.е. таких, что 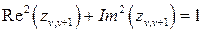 , то имеет место колебательная граница устойчивости. В этом случае с течением времени в системе устанавливаются незатухающие колебания. Например, если бы в решении разностного уравнения (10.8)
, то имеет место колебательная граница устойчивости. В этом случае с течением времени в системе устанавливаются незатухающие колебания. Например, если бы в решении разностного уравнения (10.8) 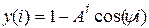 модуль комплексных сопряженных корней А был равен 1, то это привело бы к незатухающим колебаниям с частотой
модуль комплексных сопряженных корней А был равен 1, то это привело бы к незатухающим колебаниям с частотой 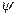 . Вещественная часть указанных корней Re(zv,v+1) может быть положительной, как на рис.12.1 г, отрицательной или нулевой.
. Вещественная часть указанных корней Re(zv,v+1) может быть положительной, как на рис.12.1 г, отрицательной или нулевой.
Типичной для импульсных систем является так называемая граница устойчивости третьего типа, которой соответствует наличие в характеристическом уравнении корня zv= -1 (рис. 12.1 д). В этом случае в системе с течением времени устанавливаются незатухающие периодические колебания с периодом 2Т, так как составляющая решения (10.16) 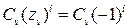 при изменении i последовательно принимает значение
при изменении i последовательно принимает значение 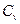 и ‑
и ‑ 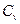 .
.
Для оценки устойчивости и качества импульсных систем используются передаточные функции разомкнутой системы W(z) и передаточные функции замкнутой системы Ф(z) или Фх(z). В соответствии с выражениями (11.23) или (11.24) характеристическое уравнение замкнутой системы (12.1) может быть получено следующим образом:
1+W(z)=0; Þ B(z)+C(z)=0, (12.2)
где B(z) и C(z) – полиномы числителя и знаменателя передаточной функции W(z).
Дата добавления: 2022-05-27; просмотров: 105;










