Уравнение Бернулли для потока реальной жидкости
При решении различных практических вопросов приходится иметь дело не с элементарными струйками, а с потоком реальной жидкости конечных размеров.
В этом случае уравнение Бернулли может быть получено путем суммирования элементарных струек.
Рассмотрим движение жидкости в канале переменного сечения при следующих допущениях:
1. Поток движущейся жидкости установившийся, т.е. 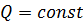 , и подчиняется основному закону гидростатики:
, и подчиняется основному закону гидростатики: 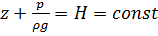 .
.
2. Затраты энергии на преодоление сопротивлений движению вязкой жидкости учитываются между сечениями потока величиной 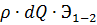 (рис.2.13).
(рис.2.13).
3. Кинетическая энергия определяется через среднюю скорость потока:
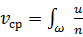 ,
,
где 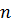 – число струек;
– число струек;
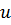 – скорость в любой струйке.
– скорость в любой струйке.
Рис.2.13
4. Жидкость несжимаема 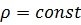 .
.
Умножив все члены уравнения для элементарной струйки с учетом потерь энергии на 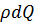 , получим:
, получим:
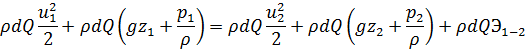
Суммируя по площади живого сечения, имеем:
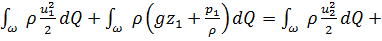
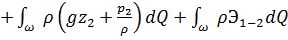 . (2.28)
. (2.28)
Рассмотрим каждый член уравнения отдельно.
Выражения
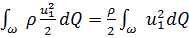
и
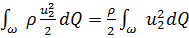
представляют собой кинетическую энергию всей массы жидкости, протекающей в единицу времени через поперечные сечения 1-1 и 2-2.
Однако
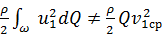 и
и 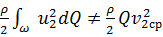 .
.
Объясняется это тем, что 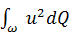 есть арифметическая сумма произведений расходов отдельных элементарных струек
есть арифметическая сумма произведений расходов отдельных элементарных струек  на квадраты их действительных скоростей
на квадраты их действительных скоростей 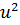 .
.
Произведение 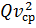 – суммарный расход потока:
– суммарный расход потока:
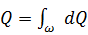 ,
,
умноженный на среднюю скорость потока:
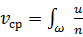 ,
,
где 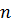 – число струек.
– число струек.
Подобная замена требует корректировки кинетической энергии потока в выражении 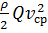 . Эта корректировка представляет собой отношение действительной кинетической энергии жидкости, протекающей через поперечное сечение потока в единицу времени, к кинетической энергии, которая имела бы место при том же расходе, если бы скорость жидкости во всех струйках была бы одинаковой и равнялась средней скорости, т.е. вводится коэффициент
. Эта корректировка представляет собой отношение действительной кинетической энергии жидкости, протекающей через поперечное сечение потока в единицу времени, к кинетической энергии, которая имела бы место при том же расходе, если бы скорость жидкости во всех струйках была бы одинаковой и равнялась средней скорости, т.е. вводится коэффициент
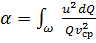 – коэффициент Кориолиса.
– коэффициент Кориолиса.
С учетом того, что 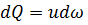 и
и 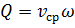 , получим
, получим
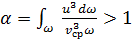 .
.
Обычно коэффициент Кориолиса определяется опытным путем на основании измерений скорости в различных точках исследуемого потока. Коэффициент 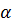 всегда больше единицы.
всегда больше единицы.
Для так называемого ламинарного режима движения жидкости в цилиндрической трубе коэффициент 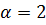 , а для турбулентного
, а для турбулентного 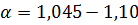 .
.
Таким образом,
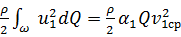 (2.29а)
(2.29а)
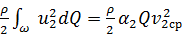 (2.29б)
(2.29б)
Рассмотрим выражение второго члена уравнения (2.28), представляющего собой потенциальную энергию потока:
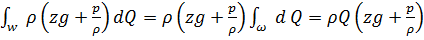 . (2.30)
. (2.30)
Третий член уравнения (2.28) представляет собой сумму работ сил сопротивления.
Подразумевая под 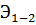 осредненное значение потерь удельной энергии, получим
осредненное значение потерь удельной энергии, получим
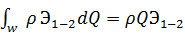 . (2.31)
. (2.31)
Подставляя выражения (2.29) и (2.31) в уравнение (2.28), получим:
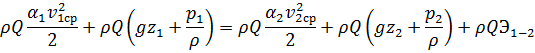
Сокращая на 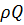 , после преобразования имеем:
, после преобразования имеем:
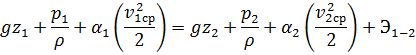
или
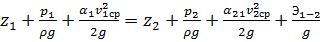 , (2.32)
, (2.32)
где 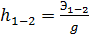 – потери напора, м.
– потери напора, м.
В общем виде уравнение Бернулли для потока вязкой жидкости принимает форму
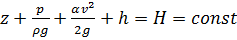 , (2.33)
, (2.33)
где 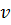 – подразумеваемая средняя скорость потока.
– подразумеваемая средняя скорость потока.
При практических расчетах часто принимают 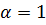 , тем самым пренебрегают неравномерностью распределения скоростей.
, тем самым пренебрегают неравномерностью распределения скоростей.
Рассмотрим геометрический смысл уравнения Бернулли для потока жидкости, обладающей вязкостью (рис.2.14).
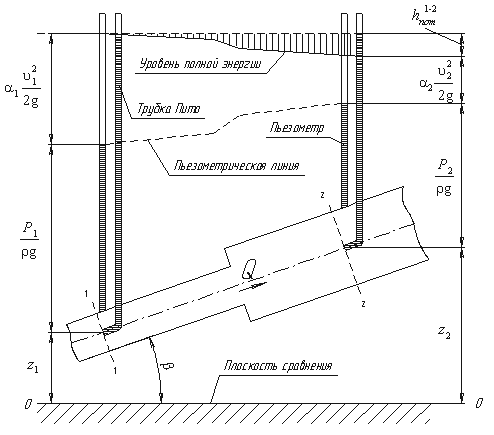
Рис.2.14
Сумма 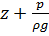 в каждом сечении является пьезометрическим напором
в каждом сечении является пьезометрическим напором 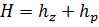 .
.
Линия, соединяющая отметки показаний пьезометров, называется пьезометрической линией.
Величина 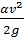 называется скоростным напором
называется скоростным напором 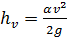 .
.
Сумма пьезометрического и скоростного напоров называется гидродинамическим, или полным напором, который можно выразить зависимостью
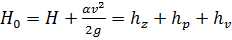 .
.
Линия, соединяющая отметки гидродинамических напоров вдоль движения, называется напорной линией, а ее уклон – гидравлическим уклоном 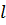 .
.
Величина 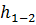 в уравнении Бернулли представляет потери напора. Если потери напора отнести к единице длины потока, то получим гидравлический уклон.
в уравнении Бернулли представляет потери напора. Если потери напора отнести к единице длины потока, то получим гидравлический уклон.
В горизонтальных напорных трубках потери напора возникают при уменьшении давления:
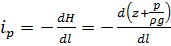 –пьезометрический уклон;
–пьезометрический уклон;
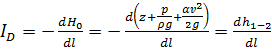 –гидравлический уклон.
–гидравлический уклон.
2.12. Гидравлические сопротивления.
Режимы движения жидкости
При движении реальных жидкостей в различных гидросистемах требуется точная оценка потерь напора на преодоление гидравлических сопротивлений. Точный учет этих потерь во многом определяет надежность технических расчетов. Кроме того, это позволяет найти экономически целесообразное инженерное решение, обладающее достаточной степенью совершенства. Для этого необходимо иметь ясное представление о механизме движения жидкости.
В процессе исследований известный физик Рейнольдс в 1883 году подтвердил теорию о существовании двух режимов движения жидкости. Это прежде всего ламинарный режим движения жидкости, соответствующий малым скоростям. Ламинарное движение можно рассматривать как движение отдельных слоев жидкости, происходящее без перемешивания частиц.
При более высоких скоростях движения жидкости наблюдается турбулентный режим («турбулентус» по - латыни – вихревой). Такое движение называют беспорядочным.
Для оценки режима движения жидкости Рейнольдс ввел безразмерный критерий 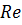 , который учитывает влияние скорости
, который учитывает влияние скорости 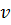 , диаметра (характерного размера)
, диаметра (характерного размера) 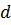 , плотности
, плотности 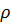 , а также динамической вязкости
, а также динамической вязкости 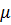 :
:
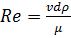 или
или 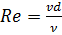 ;
;
где 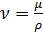 – кинематическая вязкость.
– кинематическая вязкость.
Граница существования того или иного режима движения жидкости определяется двумя критическими значениями числа 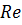 : нижним
: нижним 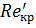 и верхним
и верхним 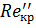 .
.
Так, при 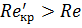 возможен только ламинарный режим, а при
возможен только ламинарный режим, а при 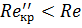 – только турбулентный режим, при
– только турбулентный режим, при 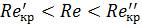 наблюдается неустойчивое состояние потока.
наблюдается неустойчивое состояние потока.
При расчетах принято исходить из одного критического значения числа 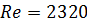 , что приводит к большей надежности в гидравлических расчетах. Критерий Рейнольдса удобен тем, что может применяться для любой формы живого сечения через гидравлический радиус. Например, для круглого сечения
, что приводит к большей надежности в гидравлических расчетах. Критерий Рейнольдса удобен тем, что может применяться для любой формы живого сечения через гидравлический радиус. Например, для круглого сечения
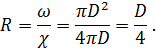
Тогда
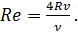 (2.34)
(2.34)
Для сечения прямоугольной формы со сторонами 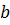 и
и 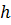
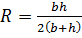 .
.
Тогда
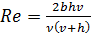 .
.
Критерий Рейнольдса является мерой отношения кинетической энергии жидкости к работе сил вязкого трения. От критерия Рейнольдса в общем случае зависят все безразмерные коэффициенты, входящие в расчетные зависимости, которые применяются в практике гидравлических расчетов.
2.13. Потери напора при равномерном движении
Рассмотрим равномерное движение в трубопроводе при следующих условиях:
1. Ускорение потока равно нулю, следовательно, силы инерции отсутствуют.
2. Cредние скорости во всех поперечных сечениях одинаковы.
3. Местные сопротивления отсутствуют. Существуют сопротивления по длине, вызывающие соответствующие потери напора на трение (рис.2.15).
Рис.2.15
4. Закон распределения давления между сечениями 1-1 и 2-2 подчиняется гидростатическому, т.е.
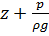 =const .
=const .
5. На объем жидкости между сечениями 1-1 и 2-2 действуют силы внешнего давления 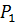 и
и 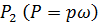 , сила тяжести
, сила тяжести 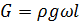 и сила сопротивления движению
и сила сопротивления движению 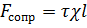 .
.
Пользуясь принципом Д’Аламбера, напишем уравнение динамического равновесия для массы жидкости, заключенной между сечениями 1-1 и 2-2 на оси 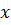 :
:
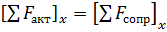 .
.
В состав активных сил входят:
1. Сила земного притяжения 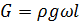 , проекция которой на ось
, проекция которой на ось 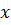 равна:
равна:
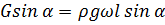
Так как 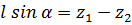 , то получаем
, то получаем
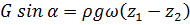 (2.35)
(2.35)
2. С учетом допущения п.4, равнодействующие сил давления 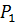 и
и 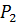 приложены в центрах тяжести сечений 1-1 и 2-2 и равны:
приложены в центрах тяжести сечений 1-1 и 2-2 и равны:
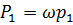 и
и 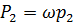 .
.
Тогда сумма проекций на ось 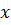
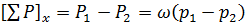 . (2.36)
. (2.36)
3. Нормальные силы к оси 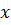 равны и противоположно направлены, поэтому проекции сил
равны и противоположно направлены, поэтому проекции сил 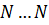 равны нулю.
равны нулю.
Очевидно, что левая часть уравнения (2.35) составляет две силы, а именно:
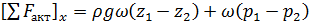 . (2.37)
. (2.37)
Силы сопротивления 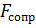 определяются по касательным напряжениям на стенке канала. Эти силы направлены параллельно оси потока в сторону, обратную движению жидкости
определяются по касательным напряжениям на стенке канала. Эти силы направлены параллельно оси потока в сторону, обратную движению жидкости
Рис. 2.16
Обозначим силу сопротивления на элементарную площадку 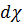 через
через 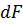 , тогда для участка трубы
, тогда для участка трубы 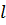 имеем:
имеем:
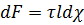 . (2.38)
. (2.38)
После интегрирования, принимая 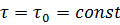 (
( 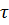 может изменяться по периметру) в выражении (2.38), получим
может изменяться по периметру) в выражении (2.38), получим
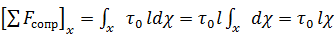 , (2.39)
, (2.39)
где 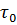 – среднее значение касательного напряжения на стенке.
– среднее значение касательного напряжения на стенке.
С учетом уравнений (2.37) и (2.39) запишем уравнение динамического равновесия в виде
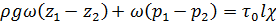 . (2.40)
. (2.40)
Разделив члены уравнения (2.40) на 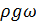 , получим
, получим
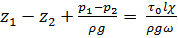 . (2.41)
. (2.41)
Обозначим отношение 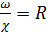 , после преобразования выражения (2.41), имеем
, после преобразования выражения (2.41), имеем
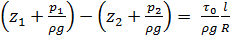 , (2.42)
, (2.42)
Сравним уравнение Бернулли, записанное для сечений 1-1 и 2-2:
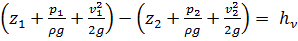 . (2.43)
. (2.43)
Так как при равномерном движении 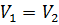 , то из сопоставления уравнений (2.42) и (2.43) находим
, то из сопоставления уравнений (2.42) и (2.43) находим
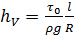 . (2.44)
. (2.44)
Учитывая, что 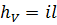 (где
(где 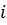 – гидравлический уклон), преобразуем выражение (2.44) к виду
– гидравлический уклон), преобразуем выражение (2.44) к виду
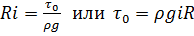 . (2.45)
. (2.45)
Это уравнение академик Н.Н.Павловский назвал основным уравнением равномерного движения.
Опытным путем Шези установлено, что величина 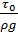 пропорциональна квадрату скорости, т.е.
пропорциональна квадрату скорости, т.е.
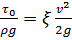 , (2.46)
, (2.46)
где 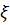 – коэффициент пропорциональности, в общем случае величина переменная.
– коэффициент пропорциональности, в общем случае величина переменная.
Подставив равенство (2.46) в выражение (2.44), получим формулу Вейсбаха.
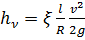 .
.
Учитывая, что 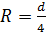 , преобразуем формулу Вейсбаха к виду
, преобразуем формулу Вейсбаха к виду
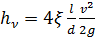 .
.
Обозначим 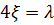 , получим
, получим
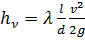 , (2.47)
, (2.47)
где 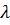 – коэффициент гидравлического трения.
– коэффициент гидравлического трения.
Формула (2.47) именуется формулой Дарси-Вейсбаха. Она используется для расчета трубопроводов.
Учитывая, что 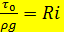 и
и 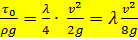 , получим
, получим
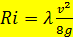 .
.
Отсюда
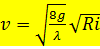 .
.
Обозначив 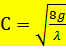 ; м/с, получим формулу Шези
; м/с, получим формулу Шези
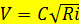 ,
,
где  – коэффициент Шези.
– коэффициент Шези.
Формула Шези получила широкое применение в расчетах открытых потоков.
Анализ формулы (2.47) показывает, что потери пропорциональны квадрату скорости, а закон сопротивления называется законом квадратичного сопротивления.
В то же время установлено, что потери напора, помимо скорости, зависят от характера режима, формы и размеров сечения, вязкости жидкости, материала и состояния стенок.
Это не учитывается формулами Шези и Дарси-Вейсбаха.
На графике (рис.3.18) показана зависимость потерь на трение в зависимости от скорости движения жидкости 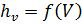 . Однако квадратичные формулы Шези и Дарси-Вейсбаха очень удобны для практических целей и обычно применяются как для турбулентного, как и для ламинарного режимов течения жидкости.
. Однако квадратичные формулы Шези и Дарси-Вейсбаха очень удобны для практических целей и обычно применяются как для турбулентного, как и для ламинарного режимов течения жидкости.
Рис.3.18
Отклонения от квадратичного закона учитываются тем, что коэффициенты 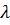 и
и 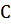 ставятся в косвенную зависимость от скорости. Поэтому основная задача при определении потерь на трение при равномерном движении жидкости сводится к определению коэффициентов
ставятся в косвенную зависимость от скорости. Поэтому основная задача при определении потерь на трение при равномерном движении жидкости сводится к определению коэффициентов 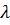 и
и 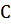 при известной скорости движения жидкости.
при известной скорости движения жидкости.
2.14. Способы определения потерь напора
при равномерном движении жидкости
Основной формулой при расчете напорных трубопроводов является формула Дарси-Вейсбаха:
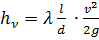 ,
,
а при расчете течений в открытых руслах – формула Шези:
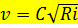 .
.
Применение этих формул связано с определением коэффициентов 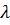 и
и  .
.
При ламинарном движении жидкости коэффициент 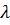 для труб определяется по формуле
для труб определяется по формуле
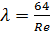 . (2.48)
. (2.48)
Впервые наиболее исчерпывающие данные о значении 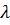 были получены Никурадзе. Результаты показаны на рис.3.19.
были получены Никурадзе. Результаты показаны на рис.3.19.
Рис.3.19
В пределах прямой 1 коэффициент 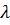 зависит не от шероховатости стенок трубы, а от числа
зависит не от шероховатости стенок трубы, а от числа 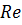 (см. формулу 2.48). Прямая 2 представляет зависимость
(см. формулу 2.48). Прямая 2 представляет зависимость 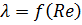 для гидравлических гладких труб, у которых шероховатость меньше толщины ламинарного пристенного слоя.
для гидравлических гладких труб, у которых шероховатость меньше толщины ламинарного пристенного слоя.
Коэффициент 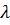 для гидравлических гладких труб определяется по формуле Блазиуса (прямая 2):
для гидравлических гладких труб определяется по формуле Блазиуса (прямая 2):
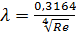 (2.49)
(2.49)
Между линиями 2 и линией 3 слева располагается зона 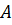 , в которой
, в которой 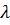 зависит как от числа Рейнольдса, так и от шероховатости поверхности стенок труб.
зависит как от числа Рейнольдса, так и от шероховатости поверхности стенок труб.
Для определения  в этой области может применяться формула А.Д.Альтшуля:
в этой области может применяться формула А.Д.Альтшуля:
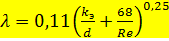 , (2.50)
, (2.50)
где 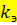 – эквивалентная равномерно зернистая шероховатость, определяемая опытным путем.
– эквивалентная равномерно зернистая шероховатость, определяемая опытным путем.
В области 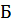 коэффициент
коэффициент 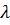 зависит только от шероховатости.
зависит только от шероховатости.
Для определения  в этой области рекомендуется формула Никурадзе
в этой области рекомендуется формула Никурадзе
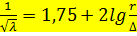 , (2.51)
, (2.51)
где 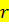 – радиус трубы;
– радиус трубы;  - абсолютная шероховатость стенок трубы.
- абсолютная шероховатость стенок трубы.
Существуют формулы Ф.А.Шевелева, Н.З.Френкеля, Л.А.Тепакса, Б.Н.Шифринсона, Н.Ф.Федорова и других.
2.15. Местные гидравлические сопротивления
Местные сопротивления вызываются фасонными частями, арматурой и другими элементами трубопровода. При движении жидкости на местных сопротивлениях изменяется величина и направление скорости.
Потери, связанные с преодолением местных сопротивлений, пропорциональны кинетической энергии потока:
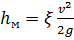 , (2.52)
, (2.52)
где 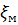 – коэффициент местных сопротивлений зависит не только от вязкости и скорости движения основного потока, но главным образом от геометрической формы и размеров сопротивления.
– коэффициент местных сопротивлений зависит не только от вязкости и скорости движения основного потока, но главным образом от геометрической формы и размеров сопротивления.
При турбулентном режиме движения жидкости потери 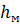 зависят только от геометрических характеристик сопротивления.
зависят только от геометрических характеристик сопротивления.
Рассмотрим вопрос о потере напора при внезапном расширении трубопровода (рис.3.20). Часть энергии в этом случае расходуется на сложное циркуляционное движение жидкости в кольцевом пространстве между струей и стенками трубы за сечением 1-1.
Рис.3.20
Вследствие отрыва потока и связанного с ним вихреобразования на участке трубы между сечениями 1-1 и 2-2 наблюдаются значительные потери напора.
Учитывая, что давление на торцевой стенке 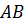 практически равно давлению на выходе из узкой части трубы
практически равно давлению на выходе из узкой части трубы 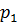 , найдем величину потерь по уравнению Бернулли:
, найдем величину потерь по уравнению Бернулли:
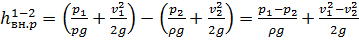 (2.53)
(2.53)
Из теоремы импульсов для сечений 1-1 и 2-2 можно записать:
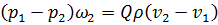 . (2.54)
. (2.54)
Вывод (2.54):
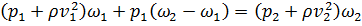
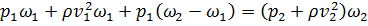
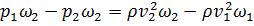
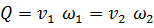
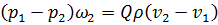
----------------------------------------------------------------------------------------------------
Пренебрегая силами трения на участке 1-2 и учитывая, что 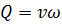 , после деления на
, после деления на 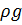 обеих частей уравнения (2.54) получим:
обеих частей уравнения (2.54) получим:
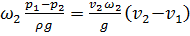
или
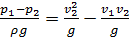 . (2.55)
. (2.55)
Подставляя выражение (2.55) в уравнение (2.53), найдем:
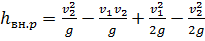
или
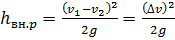 . (2.56)
. (2.56)
То есть, потери напора при внезапном расширении равны скоростному напору от потерянной скорости. Выражение (2.56) называется теоремой, или формулой Борда.
Формулу (2.56) можно привести к виду:
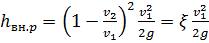 .
.
С учетом того, что 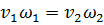 и
и 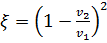 , получим:
, получим:
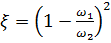 – относится к скорости
– относится к скорости 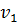 ;
;
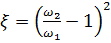 – относится к скорости
– относится к скорости 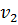 .
.
Суммарные потери напора в трубопроводе постоянного диаметра 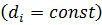
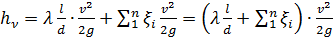 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| ОСНОВЫ КИНЕМАТИКИ И ДИНАМИКИ ЖИДКОСТИ | | | Физическая сущность гидравлического удара |
Дата добавления: 2016-06-05; просмотров: 4408;










