Теорема сложения вероятностей несовместных событий.
Теорема сложения вероятностей несовместных событий. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Р(А + В) = Р(А) + Р(В).
Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
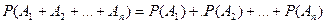
Теорема сложения вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
P (A+B) = P(A) + P(B) – P(AB)
Теорема может быть обобщена на любое конечное число совместных событий. Например, для трех совместных событий.
P(A+B+C) = P(A) + P(B) + P(C) – P(AB) – P(AC) – P(BC) + P(ABC)
Теорема умножения вероятностей.Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
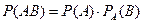
В частности, для независимых событий
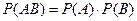
т.е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.
Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляют в предложении, что все предыдущие события уже наступили:
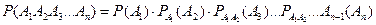
где 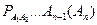 – вероятность события Ап, вычисленная в предположении, что события
– вероятность события Ап, вычисленная в предположении, что события 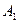 ,
, 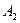 , ....,
, ...., 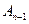 наступили.
наступили.
В частности, вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
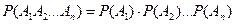
Дата добавления: 2016-06-05; просмотров: 3753;










