Дискриминантный анализ

Дискриминантный анализ – это общий термин, относящийся к нескольким тесно связанным статистическим процедурам.

Эти процедуры можно разделить на методы интерпретации межгрупповых различий и методы классификации наблюдений (объектов) по группам.

Основным предположением дискримнантного анализа является то, что существуют две или более группы (классы, таксоны, кластеры, множества, совокупности), которые по некоторым параметрам отличаются между собой.

Основная задача дискриминантного анализа часто состоит в определении по результатам наблюдений, какой из возможных групп принадлежит объект, случайно извлеченный из одной из них. Метод используется, когда информация об истинной принадлежности объекта недоступна, требует разрушения объекта или чрезмерных материальных затрат и времени.

Основные ограничения, касающиеся статистических свойств дискриминантных переменных, т.е. показателей, с помощью которых описываются объекты в группах, сводятся к следующему.

1. Ни одна переменная 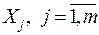не может быть линейной комбинацией других переменных.

2. Ковариационные матрицы дискриминантных переменных 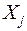для генеральных совокупностей равны между собой для различных групп. Это обеспечивает возможность использования для принятия решений о классификации линейных дискриминантных функций.

3. Закон распределения дискриминантных переменных для каждого класса является многомерным нормальным, т.е. каждая переменная имеет нормальное распределение при фиксированных остальных переменных. Данное предположение позволяет получить точные значения вероятности принадлежности объектов к данной группе и критерия значимости.

Пусть имеются две или более генеральные совокупности 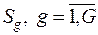с известными или оцениваемыми по выборкам распределениями. Получена реализация какой–то из рассматриваемых многомерных СВ, характеризующих соответствующую совокупность.

Задача дискриминации (различения, идентификации) состоит в построении правила, позволяющего приписать полученную реализацию (или объект) к определенной совокупности, т.е. идентифицировать этот новый объект.

Решение задачи дискриминации состоит в разбиении всего выборочного пространства всех возможных реализаций изучаемых СВ на некоторое число областей. При попадании идентифицируемого объекта в соответствующую область этот объект приписывается к соответствующей генеральной совокупности.

Границы указанных областей должны быть по возможности простыми (например, гиперплоскостями) и выбраны таким образом, чтобы уменьшить потери от ложной дискриминации.

Часто информация о распределениях генеральных совокупностей представлена независимыми выборками из них. Такие выборки называются обучающими выборками.

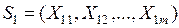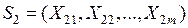Рассмотрим две нормально распределенные m–мерные генеральные совокупности и с математическими ожиданиям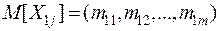и и 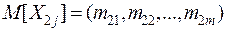и одинаковыми ковариационными матрицами _.

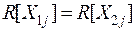Если 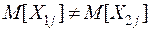(т.е центры совокупностей не совпадают), то выборочное пространство случайных величин 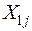и 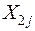можно разделить на две области и 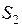гиперплоскостью

.

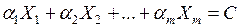Левая часть уравнения 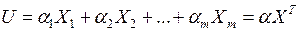называется дискриминантной функцией. Здесь 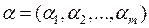вектор коэффициентов дискриминантной функции.

Област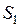и и 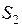можно задать неравенствами , .

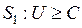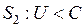Величина С называется пороговым значением.

Пусть имеется элемент выборки (или объект), которому соответствует вектор наблюдений .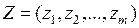

Если U(Z) і C, то Z относим к 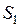, если же U(Z) < C, то Z относим к .

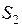Таким образом, задача дискриминации сводится к определению коэффициентов 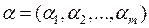дискриминантной функции U и порогового значения С (рис. 3.7.1).

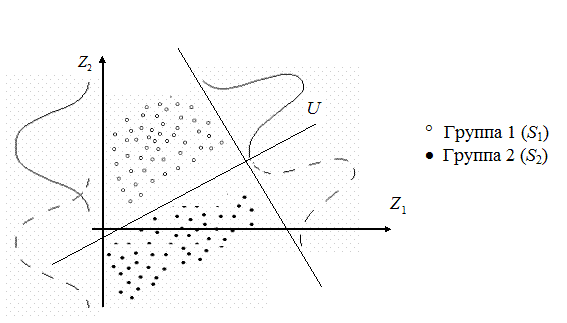
Рис.3.7.1. Графическое представление дискриминантной функции

для двух переменных и двух обучающих выборок

Алгоритмы классификации.

Рассмотрим случай .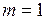

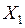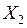Пусть имеются две генеральные совокупности одномерной величины и с известными распределениям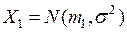и и .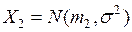

Пусть наблюдаемый объект имеет значение Z. К какой из генеральных совокупносте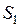й ( или 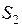) принадлежит этот объект?

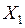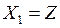Функция плотность величины при равна

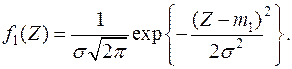
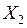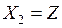Функция плотность величины при равна

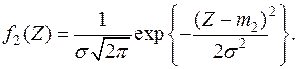
Выбираем следующий простой алгоритм классификации: если 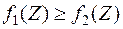, то отнесем объект к первой генеральной совокупности , если 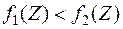, то – ко второй совокупности .

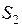Таким образом, имеем правило принятия решения:

;

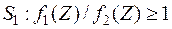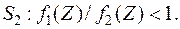
Так как 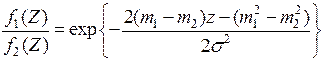, то область 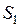задается неравенством:

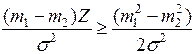
Рассмотрим теперь 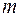–мерный случай.

Пусть имеются две генеральные совокупности величин 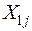и 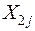с известными 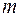–мерными распределениям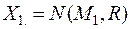и и .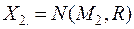

Для вектора наблюдений 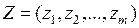плотности вероятностей этих величин равны соответственно

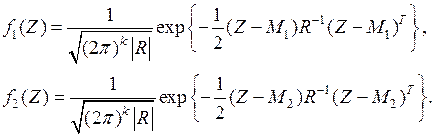
Област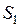и и 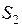определяются аналогично:

;

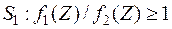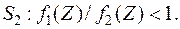
Для области 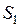получаем обобщение неравенства (10.1)

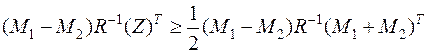
Если обозначить

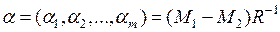и 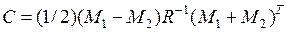, то неравенство (10.2) превращается в неравенство

,

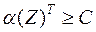где 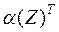– дискриминантная функция, С – пороговое значение.

Предположим теперь, что известны априорные вероятност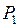и и 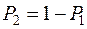того, что случайно наблюдаемый объект принадлежит соответственно к первой генеральной совокупности или ко второй.

Пусть также известны стоимости ошибочной классификации:

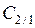– стоимость потерь из–за отнесения ко второй генеральной совокупности вектора наблюдений 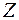, принадлежащего к первой генеральной совокупности;

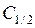– стоимость потерь из–за отнесения к первой генеральной совокупности вектора наблюдений 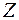, принадлежащего ко второй генеральной совокупности.

Тогда по теореме Байеса наблюдаемый вектор 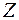будет принадлежать первой совокупности 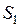с вероятностью

,

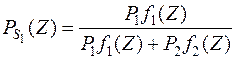а второй совокупности с вероятностью

.

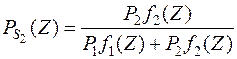Тогда, если мы отнесем вектор наблюдений 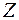к первой совокупности 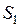, то математическое ожидание потерь составит

.

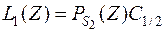Если отнести вектор наблюдений z ко второй совокупности 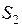, то математическое ожидание потерь составит

.

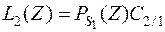В качестве алгоритма классификации примем

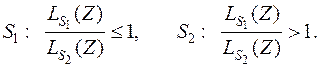
Несложно определить, что область 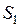задается неравенством

.

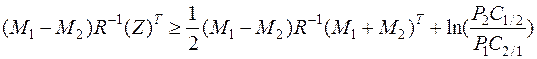Если какая–либо априорная информация о генеральных совокупностях отсутствует, то обычно полагают ; .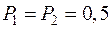

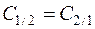Тогда неравенство (10.3) переходит в неравенство (10.2).

Если 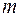–мерные векторы математических ожиданий 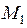, 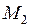и ковариационная матрица R генеральных совокупностей неизвестны, то по обучающим выборкам 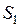и 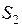находят оценки этих параметров.

В этом случае оценка ковариационной матрицы вычисляется по формуле

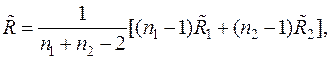
где 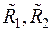– несмещенные оценки ковариационных матриц ;

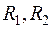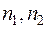– объемы выборок из 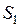и 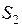соответственно.

Рассмотрим задачу дискриминации для случая G нормально распределенных генеральных совокупностей .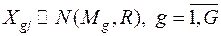

Дискриминантную функцию i –й и q –й совокупностей можно записать в виде

.

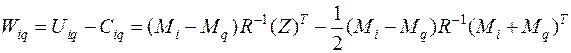Если параметры генеральных совокупностей неизвестны, то вычисляют их оценки по соответствующим обучающим выборкам, причем

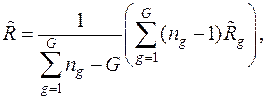
где 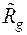– несмещенная оценка ковариационной матрицы ;

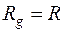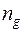– объем выборки из 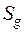–й совокупности, .

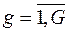Если для всех q № i выполняется неравенство 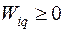, то наблюдаемый вектор относят к совокупности .

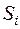Дискриминантный анализ широко используется во многих прикладных исследованиях: психологическое тестирование взрослых и детей; тестирование при приеме на работу; анализ переписи населения; изучение эффектов какого–либо метода лечения; изучение экономических различий между фирмами, географическими районами; социологические исследования и др.

Считается, что наилучшим правилом классификации является байесовское решающее правило, обеспечивающие минимальные средние потери от неправильной классификации и основанные на отношении апостериорных вероятностей различных классов в данной точке пространства признаков.

На практике эти отношения оцениваются по обучающей выборке (наблюдениям с известной классификацией) с помощью параметрических и непараметрических методов.

Примером могут служить линейные дискриминантные функции Р.Фишера для нормальных распределений или метод "ближайшего соседа".

Другим возможным методом дискриминантного анализа является минимизация оценки среднего риска или метод "скользящего экзамена" в заранее заданном классе решающих правил.

Линейная дискриминантная функция Р.Фишера – такая линейная комбинация признаков, среднее значение которой в разных классах, отнесенное к ее квадратичному отклонению максимально различается.

Для нормальных распределений, отличающихся только средними, дискриминантная функция задает байесовское правило классификации.

В дискриминантном анализе нескольких классов для реализации байесовского решающего правила надо рассматривать несколько функций, позволяющие сравнивать апостериорные вероятности классов.

Кластерный анализ

Рассматривается некоторая выборка наблюдаемых показателей

.

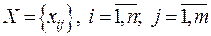Задача состоит в классификации элементов выборки (объектов) по группам (классам, кластерам, таксонам, множествам) так, чтобы объекты внутри групп были схожими ("близкими" по соответствующим характеристикам), а сами группы были бы максимально различными (разделенными), насколько это возможно.

Критерием классификации является некоторая функция "близости" или расстояние между объектами.

Например, при классификации показателей характеристикой расстояния между 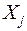и 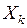часто является коэффициент корреляции 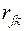, т.е. в этом случае функция "близости" или "расстояние" между 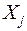и 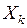может быть задана в виде:

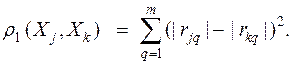
Другими примерами метрик близости являются:

евклидово расстояние между показателями

;

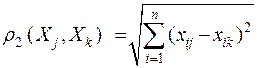расстояние между объектами

,

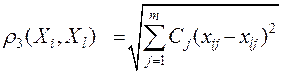где 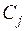– вес j–го показателя.

Расстояние Хемминга между показателями определяется выражением: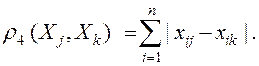

При конструировании различных кластер–процедур часто используется понятие расстояния не между отдельными объектами, а между целыми группами (классами, таксонами) объектов.

1. Расстояние между двумя группами S_i и S_j равно расстоянию между ближайшими объектами этих групп ("ближайший сосед"):

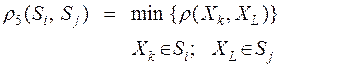
2. Расстояние между двумя группам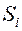и и 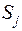равно расстоянию между их математическими ожиданиями ("центр тяжести")

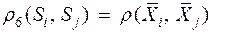
Здесь 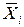– вектор математического ожидания для i–й группы.

3. Расстояние между двумя группам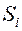и и 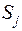равно расстоянию между самыми дальними объектами этих групп ("дальний сосед")

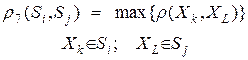
4. Расстояние между двумя группам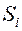и и 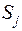равно среднему арифметическому возможных попарных расстояний между представителями рассматриваемых групп:

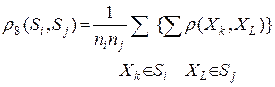
Здесь 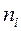– число объектов в группе .

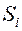На практике иногда используются иерархические кластер–процедуры. Это пошаговый алгоритм, при котором на каждом шаге происходит разбиение (объединение) множества объектов, подлежащих классификации, на (в) непересекающиеся кластеры, при этом каждое последующее разбиение (объединение) относится к кластерам, полученным на предыдущем шаге.

При работе таких процедур происходит построение так называемого иерархического классификационного дерева. Под ним понимается множество разбиений исходной выборки на классы, упорядоченные по уровням иерархии, т.е. по номеру шага иерархической процедуры.

Из сказанного следует существование двух типов процедур:

а) агломеративные, которые на каждом шаге объединяют полученные ранее кластеры в более крупные группы;

б) дивизимные, которые на каждом шаге дробят полученные ранее кластеры на более мелкие.

Примером агломеративной процедуры является пороговый алгоритм. Здесь имеется монотонно возрастающая последовательность порогов 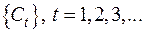и на каждом шаге t к одному классу относятся те объекты, расстояние между которыми не превосходит .

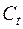К недостаткам иерархических процедур относят громоздкость их реализации на ЭВМ.

Достоинство – делают полный и достаточно тонкий анализ структуры объектов, например, при выявлении естественных групп признаков по алгоритму типа "средней связи" или "ближайшего соседа". Обнаружив такие группы можно снизить размерность описания либо выбрасыванием дублирующих (близких) признаков, либо заменив каждую группу новым показателем, общим для этой группы свойством с соответствующей интерпретацией.

Общая схема иерархической процедуры (для определенности агломеративной):

1) все объекты считаются отдельными кластерами;

2) два самых близких кластера по матрице межклассовых расстояний объединяются в один;

3) пересчитывается матрица межклассовых расстояний;

4) переход к пункту 2.

Очевидно такая процедура за n – 1 шагов (n – число объектов) объединит все объекты в один кластер.

На каждом шаге будем фиксировать расстояние между объединяемыми кластерами как функцию j(t) от номера шага t.

Такая функция будет монотонно возрастать, поскольку каждый раз происходит объединение ближайших классов, расстояние между которыми наименьшее (рис.3.8.1).

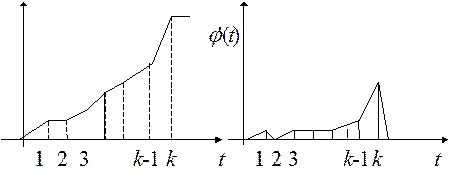
Рис.3.8.1. Принятие решения о классификации объектов

По производной j'(t) можно принять решение о том, что на шаге k – 1 была самая удачная группировка объектов, т.к. на шаге k были объединены кластеры (объекты) с большим межклассовым расстоянием (рис. 3.8.1).

Дендограмма – графическое изображение результатов кластерного анализа в виде дерева решений.