Скатывание цилиндра с наклонной плоскости
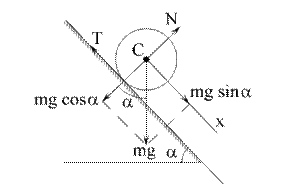 Рис. 4.5
Рис. 4.5
|
Будем считать, что скатывание цилиндра радиусом R происходит без скольжения. Силы, действующие на цилиндр, указаны на рис. 4.5. Сила Т – сила сцепления, которая обеспечивает скатывание цилиндра. Ось х удобно направить вдоль наклонной плоскости. Напишем законы движения, имея в виду, что через точку С проходит мгновенная ось вращения. Уравнения (4.11) имеют вид
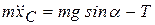 ,
, 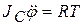 , (4.12)
, (4.12)
где 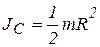 ; отсчет направлений вращения выбран так, чтобы угловая скорость
; отсчет направлений вращения выбран так, чтобы угловая скорость 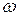 (
( 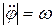 ) увеличивалась при скатывании цилиндра.
) увеличивалась при скатывании цилиндра.
Вычисляя Т из второго уравнения (4.12) и подставляя в первое, учитывая, что 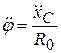 , получим
, получим
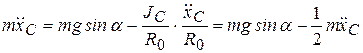 ,
,
или
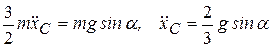 . (4.13)
. (4.13)
Таким образом, центр масс цилиндра движется с постоянным ускорением 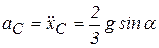 .
.
Маятник Максвелла
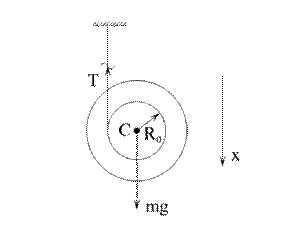 Рис. 4.6
Рис. 4.6
|
Маятник Максвелла представляет собой диск, подвешенный на нерастяжимой нити. Нить конечной длины намотана на ось диска и закреплена на оси (рис. 4.6). Уравнения движения маятника имеют вид
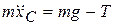 ,
, 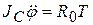 , (4.14)
, (4.14)
где 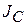 - момент инерции всего диска относительно оси, проходящей через центр масс;
- момент инерции всего диска относительно оси, проходящей через центр масс; 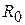 - радиус оси диска, на которую намотана нить; Т – сила натяжения.
- радиус оси диска, на которую намотана нить; Т – сила натяжения.
Структура уравнений маятника Максвелла полностью аналогична структуре уравнений цилиндра, скатывающегося с наклонной плоскости (уравнения 4.12) и решаются аналогично.
Получаем из (4.14)
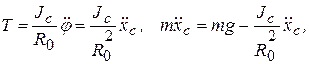
откуда
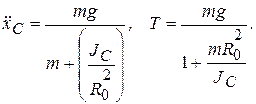 (4.15)
(4.15)
Проследим динамику движения маятника. Ускорение диска всегда постоянно и направлено вниз. Его числовое значение тем меньше, чем больше момент инерции 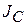 . При достаточно большом моменте инерции
. При достаточно большом моменте инерции 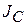 диск будет иметь малое ускорение. В пределе
диск будет иметь малое ускорение. В пределе 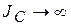 ,
, 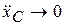 , а
, а 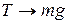 ; так и должно быть, потому что диск просто висит на нити без движения. При
; так и должно быть, потому что диск просто висит на нити без движения. При 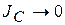 сила натяжения нити
сила натяжения нити 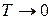 . В этом случае диск свободно падает, и поэтому нить не испытывает никакого натяжения. Уравнения (4.14) и решение (4.15) не описывают поведение маятника в нижней «мертвой» точке. В этом положении центр масс диска испытывает большое ускорение. По третьему закону Ньютона, это приводит к большому натяжению нити. Если нить недостаточно прочна, то она может в этот момент порваться.
. В этом случае диск свободно падает, и поэтому нить не испытывает никакого натяжения. Уравнения (4.14) и решение (4.15) не описывают поведение маятника в нижней «мертвой» точке. В этом положении центр масс диска испытывает большое ускорение. По третьему закону Ньютона, это приводит к большому натяжению нити. Если нить недостаточно прочна, то она может в этот момент порваться.
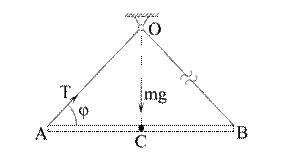 Рис. 4.7
Рис. 4.7
|
Рассмотрим еще один пример плоского движения тела.
Пример. На двух нерастяжимых невесомых нитях одинаковой длины подвешен в точке О однородный стержень АВ массой m и длиной 2L (рис.4.7). Нити со стержнем образуют углы 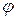 . В некоторый момент времени нить ОВ обрывается. Найти натяжение Т нити ОА непосредственно после момента обрыва.
. В некоторый момент времени нить ОВ обрывается. Найти натяжение Т нити ОА непосредственно после момента обрыва.
Решение. Движение стержня после разрыва нити плоское. В момент разрыва ускорение центра находится по теореме об ускорениях при плоском движении. За полюс выберем точку А. Вычислим ускорение центра масс стержня АВ, т.е. ускорение точки С:
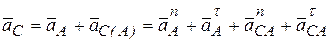 , (4.16)
, (4.16)
здесь 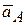 - ускорение полюса А,
- ускорение полюса А, 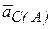 - ускорение центра масс при его вращении относительно полюса А. Поскольку точка А может двигаться только по окружности радиуса ОА, а ее скорость в момент обрыва нити равна нулю, то
- ускорение центра масс при его вращении относительно полюса А. Поскольку точка А может двигаться только по окружности радиуса ОА, а ее скорость в момент обрыва нити равна нулю, то 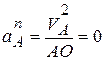 . Проекцию ускорения точки А по касательной обозначим
. Проекцию ускорения точки А по касательной обозначим 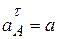 .
.
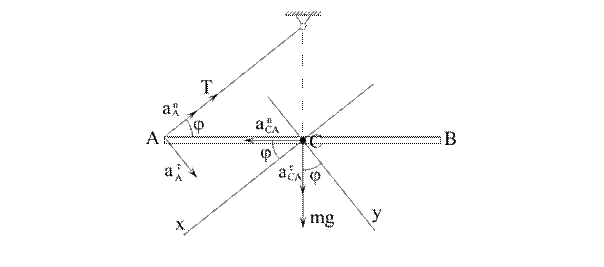 Рис. 4.8
Рис. 4.8
|
Обозначим модуль углового ускорения стержня через 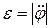 , а модуль угловой скорости через
, а модуль угловой скорости через 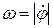 (начальный момент времени равен нулю). Тогда
(начальный момент времени равен нулю). Тогда 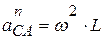 и направлена вдоль стержня от точки С к точке А;
и направлена вдоль стержня от точки С к точке А; 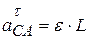 и направлена перпендикулярно стержню в точке А (рис. 4.8).
и направлена перпендикулярно стержню в точке А (рис. 4.8).
Выберем систему координат xСy, как показано на рис. 4.8. Тогда ускорение точки 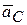 имеет следующие проекции на эти оси:
имеет следующие проекции на эти оси:
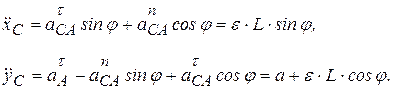 (4.17)
(4.17)
Поскольку 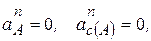 закон плоского движения (4.11) с учетом (4.17) запишется
закон плоского движения (4.11) с учетом (4.17) запишется
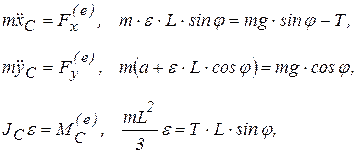 (4.18)
(4.18)
где учтено, что момент инерции стержня относительно его центра 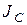 , равен
, равен  .
.
Из третьего уравнения (4.18) выразим 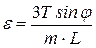 и подставим в первое уравнение, получим
и подставим в первое уравнение, получим
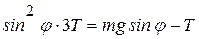 .
.
Отсюда находим
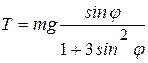 .
.
Дата добавления: 2019-12-09; просмотров: 625;










