Этапы решения задач виброзащиты
Решение задач виброзащиты машин и механизмов включает следующие этапы:
• построение модели объекта;
• формирование критериев качества;
• изучение реакции объекта на заданное внешнее воздействие;
• сравнение по заданному критерию результирующих показателей с допустимыми величинами.
Простейшие задачи виброизоляции возникают в том случае, когда совокупность сил в реальном упругом амортизаторе может быть с достаточной точностью описана как линейная функция координаты х и скорости х:
R(x, 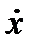 ) = -сх-ε
) = -сх-ε 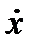 . (12.3)
. (12.3)
Коэффициент с принято называть жесткостью амортизатора, as — коэффициент вязкого трения (демпфирования). С учетом (12.3) уравнение (12.1) примет вид
m 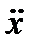 + ε
+ ε 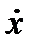 + сх = F0 cosωt(12.4)
+ сх = F0 cosωt(12.4)
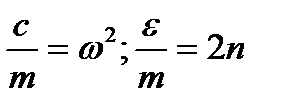
|
Обозначим и перепишем (12.4)
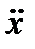 + 2п + 2п 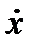 + + 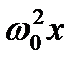 = = 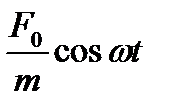
|
следующим образом: (12.5)
Ограничимся анализом работы виброзащитной системы в установившемся режиме. В этом случае решение уравнения (12.5) может быть представлено в видеx
х = A cos (ωt-γ), (12.6)
где А — амплитуда колебаний массы т; у — сдвиг фаз между колебаниями массы т и внешней силой F(t). При этом амплитуда колебаний
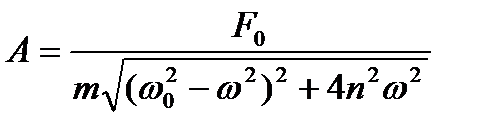
и сдвиг фаз колебаний массы т1 и силы F(t).
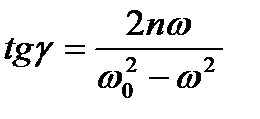
Оценку качества виброизоляции целесообразно проводить, сопоставляя амплитудное значение силы R0, развиваемой в амортизаторе и, следовательно, передаваемой на основание, с амплитудным значением внешней силы FQ.
Отношение амплитудного значения силы R0 к амплитудному значению внешней силы F0 называется коэффициентом виброизоляции 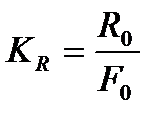
Амплитудное значение силы, развиваемой в упругом амортизаторе, показано на рис. 12.3:
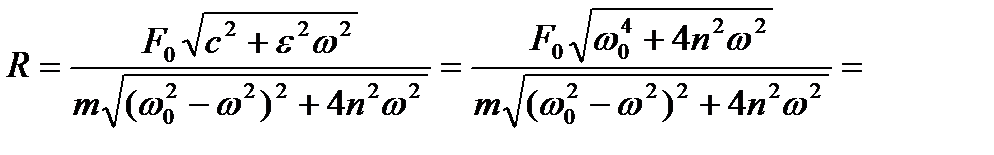
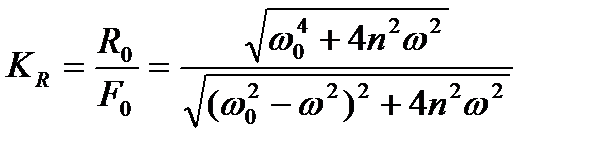
Используя понятие относительного коэффициента затухания 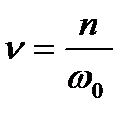 можно привести выражение KR к виду, удобному для анализа:
можно привести выражение KR к виду, удобному для анализа:
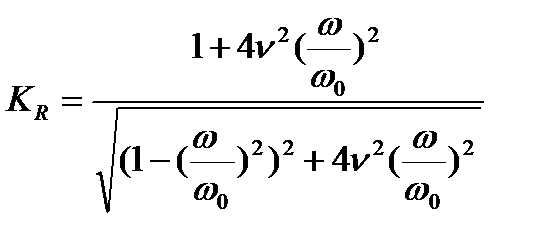
Рис. 3
Из анализа выражения (12.9) видно, что коэффициент виброизоляции KR явным образом зависит от соотношения частот (вынужденной и собственной). Для различных соотношений 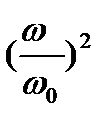 (расстройка) и V =
(расстройка) и V = 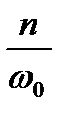 построены графики (см. рис. 3).
построены графики (см. рис. 3).
Условие эффективности виброзащиты KR < 1: при любом значении v в диапазоне 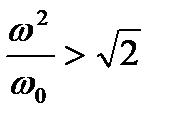 причем чем меньше ν, тем она эффективнее. На основании этого можно сделать вывод: виброизоляция эффективна для уменьшения вредного влияния вибраций в широком частном диапазоне.
причем чем меньше ν, тем она эффективнее. На основании этого можно сделать вывод: виброизоляция эффективна для уменьшения вредного влияния вибраций в широком частном диапазоне.
14.4 Кинематическое возбуждение т<<М
Если перед проектировщиком ставится задача защиты объекта, находящегося на вибрирующем основании (рис. 4), то в простейшем случае, с учетом сделанных,' выше предположений, данная задача сводится к анализу динамической схемы, представленной на рис. 1.
Рис. 4.
Дифференциальное уравнение, описывающее колебание массы т, может быть записано в виде
m 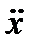 + ε(
+ ε( 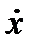 -
- 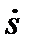 )+с(x-s) = 0
)+с(x-s) = 0
где S(t) ~ перемещение основания М.
Данное уравнение можно представить в виде
m 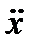 + ε
+ ε 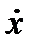 +cx=ε
+cx=ε 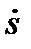 +сs =F(t) (12.10)
+сs =F(t) (12.10)
Если S(t) представляет собой монохроматические колебания, то член F(t), стоящий в правой части уравнения (12.10), приобретает смысл гармонической возмущающей силы. Очевидно, что анализ уравнения (12.10) аналогичен анализу уравнения (12.4), проведенному ранее. Совпадают и вытекающие из этого анализа рекомендации.
Дата добавления: 2018-05-10; просмотров: 1204;










