Основные типы дифференциальных уравнений первого порядка и методы их интегрирования
Как было отмечено ранее, мы рассматриваем лишь такие дифференциальные уравнения первого порядка 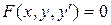 , которые можно записать в нормальной форме
, которые можно записать в нормальной форме
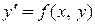 (1.1)
(1.1)
(если оно уже не записано так). В свою очередь, всякое уравнение 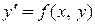 можно привести к виду
можно привести к виду
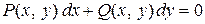 (1.2)
(1.2)
Эти две формы записи дифференциального уравнения будем называть стандартными. Всякое конкретное дифференциальное уравнение отличается от других видом функции 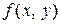 , если оно записано в форме (1.1), или видом функций
, если оно записано в форме (1.1), или видом функций 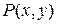 и
и 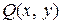 , если записано в форме (1.2).
, если записано в форме (1.2).
Например, в уравнении 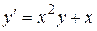 функция
функция 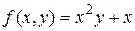 , а в уравнении
, а в уравнении 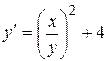 функция
функция 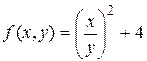 .
.
Для уравнения 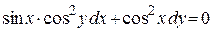 функции
функции 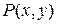 и
и 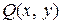 имеют вид:
имеют вид: 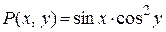 ,
, 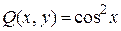 .
.
По виду функций 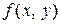 в уравнении (1.1), или функций
в уравнении (1.1), или функций 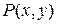 и
и 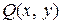 в уравнении (1.2) дифференциальные уравнения разделяются на типы. Каждый тип дифференциального уравнения имеет свой метод интегрирования.
в уравнении (1.2) дифференциальные уравнения разделяются на типы. Каждый тип дифференциального уравнения имеет свой метод интегрирования.
Рассмотрим основные типы дифференциальных уравнений первого порядка и методы их интегрирования. Ниже в таблице приведены стандартные формы записи таких уравнений (особенности входящих в них функций) и последовательность действий, приводящих к искомому решению.
| название | Вид ДУ | Метод интегрирования | ||||
| 1. Дифференциальное уравнение с разделенными переменными | 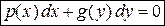
| Проинтегрировать почленно обе части уравнения
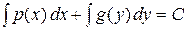 и записать общий интеграл уравнения в виде
и записать общий интеграл уравнения в виде
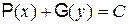 . .
| ||||
| 2. Дифференциальное уравнение с разделяющимися переменными | 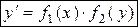
| 1) Записать производную 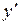 в форме в форме 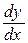 ;
2) Обе части уравнения ;
2) Обе части уравнения 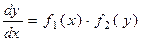 умножить на умножить на 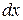 и разделить на и разделить на 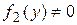 ;
3) Полученное уравнение с разделенными переменными проинтегрировать. ;
3) Полученное уравнение с разделенными переменными проинтегрировать.
| ||||
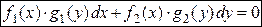 или или
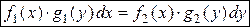
|
1) Разделить обе части уравнения на 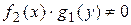 .
2) Полученное уравнение с разделенными переменными проинтегрировать. .
2) Полученное уравнение с разделенными переменными проинтегрировать.
| |||||
| 3. Однородное дифференциальное уравнение первого порядка | 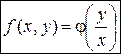
| 1) С помощью замены 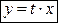 , , 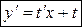 (или (или 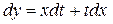 ), где ), где 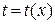 – новая неизвестная функция, привести уравнение к уравнению с разделяющимися переменными относительно функции – новая неизвестная функция, привести уравнение к уравнению с разделяющимися переменными относительно функции 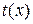 .
2) Найти общее решение .
2) Найти общее решение 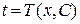 этого уравнения.
3) Вернуться к искомой функции у с помощью обратной замены этого уравнения.
3) Вернуться к искомой функции у с помощью обратной замены 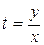 , т.е. записать: , т.е. записать: 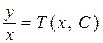 , или , или 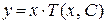 . .
| ||||
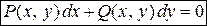 , где Функции , где Функции 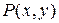 и и 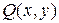 – однородные функции одного и того же измерения, т.е. – однородные функции одного и того же измерения, т.е.
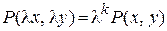 , ,
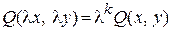 ,
где ,
где 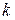 – некоторое неотрицательное целое число. – некоторое неотрицательное целое число.
| ||||||
| 4. Линейное дифференциальное уравнение первого порядка |
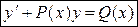
| Метод Бернулли.
1) Сделать замену 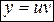 , , 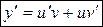 , где , где 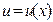 , , 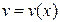 – новые неизвестные функции. Тогда уравнение примет вид – новые неизвестные функции. Тогда уравнение примет вид
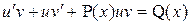 2) Преобразовать его к виду
2) Преобразовать его к виду
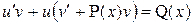 3) Составить систему уравнений:
3) Составить систему уравнений: 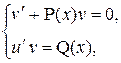 и найти частное решение и найти частное решение 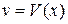 (т.е. без константы С) первого уравнения этой системы, а при найденном (т.е. без константы С) первого уравнения этой системы, а при найденном 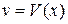 найти общее решение найти общее решение 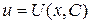 второго уравнения.
4) Записать ответ второго уравнения.
4) Записать ответ 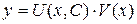 . .
| ||||
| 5. Дифференциальное уравнение Бернулли |
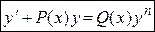
| Метод Бернулли.
1)Сделать замену 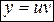 , , 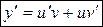 , где , где 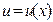 , , 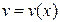 – новые неизвестные функции. Тогда уравнение примет вид – новые неизвестные функции. Тогда уравнение примет вид
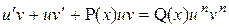 2) Преобразовать его к виду
2) Преобразовать его к виду
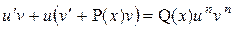 3) Составить систему уравнений:
3) Составить систему уравнений: 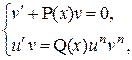 и найти частное решение и найти частное решение 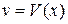 (т.е. без константы С) первого уравнения этой системы, а при найденном (т.е. без константы С) первого уравнения этой системы, а при найденном 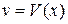 найти общее решение найти общее решение 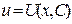 второго уравнения.
4) Записать ответ второго уравнения.
4) Записать ответ 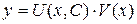 . .
| ||||
Предлагаем следующий алгоритм решения (интегрирования) дифференциального уравнения первого порядка.
1) Определить тип уравнения, например, пользуясь предложенной выше таблицей. Для этого нужно:
· привести уравнение к стандартному виду (1.1) или (1.2);
· проанализировать функции, входящие в уравнение: 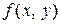 в уравнении (1.1) или
в уравнении (1.1) или 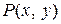 ,
, 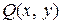 в уравнении (1.2), и выяснить, какими из основных свойств, по которым дифференциальные уравнения разделяются на типы, эти функции обладают. Например, уравнение с разделенными переменными может быть записано только в форме (1.2), причем дифференциал
в уравнении (1.2), и выяснить, какими из основных свойств, по которым дифференциальные уравнения разделяются на типы, эти функции обладают. Например, уравнение с разделенными переменными может быть записано только в форме (1.2), причем дифференциал 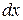 умножается на функцию, зависящую только от х, а дифференциал
умножается на функцию, зависящую только от х, а дифференциал 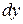 – на функцию, зависящую от у.В уравнении с разделяющимися переменными функции
– на функцию, зависящую от у.В уравнении с разделяющимися переменными функции 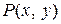 ,
, 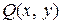 ,
, 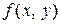 должны представлять собой произведение двух функций, одна из которых зависит от х, другая – от у. В однородном уравнении функция
должны представлять собой произведение двух функций, одна из которых зависит от х, другая – от у. В однородном уравнении функция 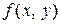 должна быть такой, что ее можно записать в виде функции отношения переменных
должна быть такой, что ее можно записать в виде функции отношения переменных 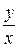 или
или 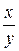 , функции
, функции 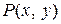 и
и 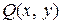 должны быть однородными функциями одного и того же измерения, и.т.д. При этом рекомендуем проверять, к какому типу относится данное дифференциальное уравнение, именно в той последовательности, в которой они указаны в таблице.
должны быть однородными функциями одного и того же измерения, и.т.д. При этом рекомендуем проверять, к какому типу относится данное дифференциальное уравнение, именно в той последовательности, в которой они указаны в таблице.
2) Выбрать метод интегрирования, соответствующий типу уравнения.
3) Применив выбранный метод, решить дифференциальное уравнение и, согласно условию задачи, записать общее или частное решение (общий или частный интеграл).
Рассмотрим примеры.
Пример 1.1.Найти общий интеграл дифференциального уравнения
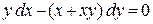 .
.
Решение:
Решим уравнение, придерживаясь указанного выше алгоритма.
1) Определим тип дифференциального уравнения. Заданное уравнение записано в форме (1.2), где 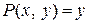 , а
, а 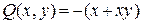 . Проанализируем эти функции и выясним сначала, является ли данное уравнение уравнением с разделенными переменными. Функция
. Проанализируем эти функции и выясним сначала, является ли данное уравнение уравнением с разделенными переменными. Функция 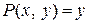 зависит только от у (а должна быть функцией от х), а
зависит только от у (а должна быть функцией от х), а 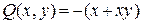 – функция двухпеременных (а должна быть функцией переменной у), следовательно, уравнением с разделенными переменными заданное уравнение не является.
– функция двухпеременных (а должна быть функцией переменной у), следовательно, уравнением с разделенными переменными заданное уравнение не является.
Если функцию 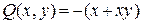 преобразовать к виду
преобразовать к виду 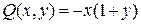 , то видим, что эта функция есть произведение двух функций:
, то видим, что эта функция есть произведение двух функций: 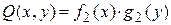 , из которых одна
, из которых одна 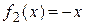 зависит только от х, а вторая
зависит только от х, а вторая 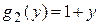 зависит только от у. Функцию
зависит только от у. Функцию 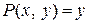 можно также считать произведением двух функций:
можно также считать произведением двух функций: 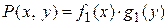 , где
, где 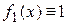 , а
, а 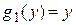 . Следовательно, данное уравнение
. Следовательно, данное уравнение
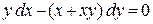 , или
, или 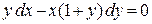 ,
,
есть дифференциальное уравнение с разделяющимися переменными.
2) «Разделим» переменные, т.е. преобразуем уравнение 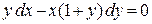 к уравнению с разделенными переменными. Для этого обе части уравнения разделим на произведение ху, чтобы коэффициентом при
к уравнению с разделенными переменными. Для этого обе части уравнения разделим на произведение ху, чтобы коэффициентом при 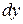 была функция переменной у, а коэффициентом при
была функция переменной у, а коэффициентом при 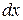 – функция от х:
– функция от х:
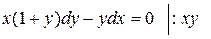 *)(ху ¹ 0).
*)(ху ¹ 0).
Получим уравнение с разделенными переменными
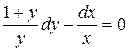 .
.
Проинтегрировав обе части этого уравнения, получим
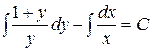 ,
,
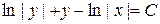 , или
, или 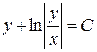
– это и есть общий интеграл данного дифференциального уравнения.
Ответ: 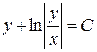
Заметим, что рассмотренное в примере 1.1 дифференциальное уравнение 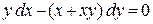 , можно рассматривать как уравнение относительно функции
, можно рассматривать как уравнение относительно функции 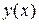 , так и относительно функции
, так и относительно функции 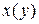 . Поэтому полученный общий интеграл
. Поэтому полученный общий интеграл 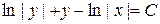 можно рассматривать как неявную функцию
можно рассматривать как неявную функцию 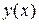 или
или 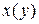 .
.
Пример 1.2. Найти решение дифференциального уравнения 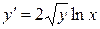
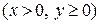 , удовлетворяющее условию
, удовлетворяющее условию 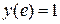 .
.
Решение: По условию задачи требуется найти частное решение уравнения, удовлетворяющее заданному начальному условию 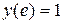 . По определению, частное решение – это решение, полученное из общего решения при конкретном значении постоянной С. Поэтому сначала найдем общее решение данного уравнения.
. По определению, частное решение – это решение, полученное из общего решения при конкретном значении постоянной С. Поэтому сначала найдем общее решение данного уравнения.
Уравнение 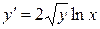 записано в нормальной форме:
записано в нормальной форме: 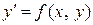 . Функция
. Функция 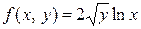 представляет собой произведение двух функций
представляет собой произведение двух функций 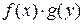 , каждая из которых зависит только от одной переменной:
, каждая из которых зависит только от одной переменной: 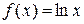 , а
, а 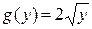 . Значит, данное дифференциальное уравнение есть уравнение с разделяющимися переменными. Следуя алгоритму (смотри таблицу 1), приведём это уравнение к уравнению с разделенными переменными
. Значит, данное дифференциальное уравнение есть уравнение с разделяющимися переменными. Следуя алгоритму (смотри таблицу 1), приведём это уравнение к уравнению с разделенными переменными 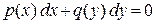 (или, что то же самое,
(или, что то же самое, 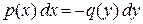 ).
).
Прежде всего, запишем производную 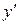 в форме
в форме 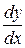 . Получим уравнение
. Получим уравнение 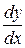 =
= 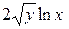 . Затем умножим обе части уравнения на
. Затем умножим обе части уравнения на 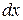 и поделим на
и поделим на 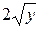 :
:
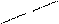
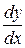 =
= 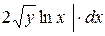 Þ
Þ 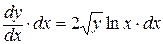 ,
,
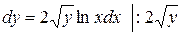 Þ
Þ 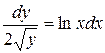 .
.
Получили уравнение с разделенными переменными. Проинтегрируем обе части этого уравнения:
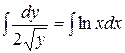 .
.
Находим: 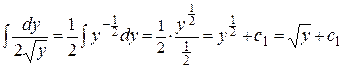 ;
;
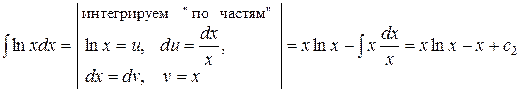 .
.
Тогда общее решение дифференциального уравнения имеет вид
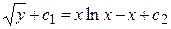 , или
, или 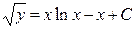 , где
, где 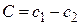 *).
*).
Теперь найдем частное решение. Чтобы определить значение постоянной С, воспользуемся начальным условием, а именно (см. алгоритм на стр. 12–13), в общее решение подставим 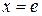 ,
, 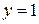 и из полученного равенства найдем значение С:
и из полученного равенства найдем значение С:
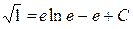 Þ
Þ 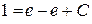 Þ
Þ 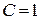 .
.
Подставив найденное значение 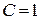 в общее решение, получим искомое частное решение:
в общее решение, получим искомое частное решение: 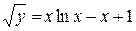 .
.
Ответ: 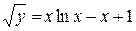 .
.
Пример 1.3. Найти общее решение дифференциального уравнения
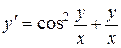 .
.
Решение
Очевидно, решение данного уравнения следует искать при 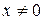 .
.
Определим тип дифференциального уравнения. Уравнение записано в нормальной форме 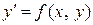 , где функция
, где функция 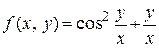 есть, очевидно, функция отношения
есть, очевидно, функция отношения 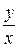 . Следовательно, данное уравнение является однородным дифференциальным уравнением первого порядка.
. Следовательно, данное уравнение является однородным дифференциальным уравнением первого порядка.
Метод интегрирования такого уравнения – метод замены переменной: 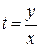 , где
, где 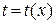 – новая неизвестная функция. Дифференциальное уравнение, получаемое в результате замены, будет уравнением с разделяющимися переменными. Итак, положим
– новая неизвестная функция. Дифференциальное уравнение, получаемое в результате замены, будет уравнением с разделяющимися переменными. Итак, положим
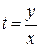 , откуда
, откуда 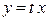 , а
, а 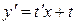 .
.
Подставив 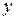 и
и 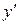 в исходное уравнение, получим дифференциальное уравнение относительно функции
в исходное уравнение, получим дифференциальное уравнение относительно функции 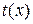 :
:
 , или
, или 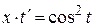 .
.
Согласно методу, это уравнение с разделяющимися переменными. «Разделим» переменные:
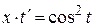 Þ
Þ 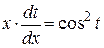 | .dx Þ
| .dx Þ
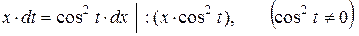 Þ
Þ
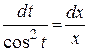 .
.
Интегрируем полученное уравнение с разделенными переменными
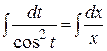 Þ
Þ 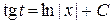 ,
,
откуда 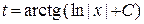 .
.
Вернемся к искомой функции 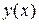 , используя равенство
, используя равенство 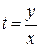 . Заменив в равенстве
. Заменив в равенстве 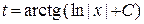 переменную t на
переменную t на 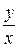 , получим общее решение исходного уравнения
, получим общее решение исходного уравнения
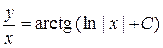 , или
, или 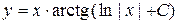 .
.
Ответ: 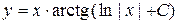 *).
*).
Пример 1. 4. Решить дифференциальное уравнение
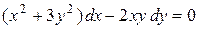
Решение
Данное дифференциальное уравнение записано в форме (1.2), где 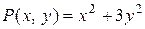 ,
, 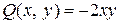 . Очевидно, это уравнение не является уравнением с разделенными переменными. Но оно не является и уравнением с разделяющимися переменными, т.к. функцию
. Очевидно, это уравнение не является уравнением с разделенными переменными. Но оно не является и уравнением с разделяющимися переменными, т.к. функцию 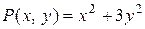 невозможно представить в виде произведения двух функций, одна из которых зависит только от переменной х, а вторая – только от у. Проверим, не является ли это уравнение однородным дифференциальным уравнением. Для этого проверим однородность функций
невозможно представить в виде произведения двух функций, одна из которых зависит только от переменной х, а вторая – только от у. Проверим, не является ли это уравнение однородным дифференциальным уравнением. Для этого проверим однородность функций 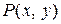 и
и 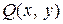 . Имеем
. Имеем
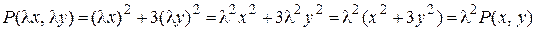 ,
,
значит 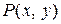 – однородная функция второго измерения (таблица 1, пункт 3). Аналогично,
– однородная функция второго измерения (таблица 1, пункт 3). Аналогично,
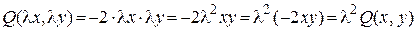 ,
,
значит, и 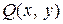 есть однородная функция второго измерения.
есть однородная функция второго измерения.
Таким образом, функции 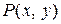 и
и 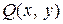 – однородные функции одного и того же измерения, следовательно, данное уравнение есть однородное дифференциальное уравнение первого порядка.
– однородные функции одного и того же измерения, следовательно, данное уравнение есть однородное дифференциальное уравнение первого порядка.
Как и в примере 1.3, для интегрирования этого уравнения применим метод замены переменной. Положим 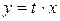 , где
, где 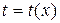 – новая неизвестная функция, при этом
– новая неизвестная функция, при этом 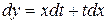 . Получим
. Получим
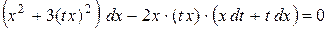 .
.
Согласно методу, полученное дифференциальное уравнение является уравнением с разделяющимися переменными. Поэтому преобразуем его сначала к виду 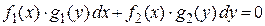 :
:
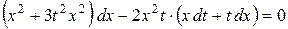 ,
,
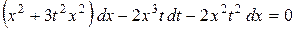 ,
,
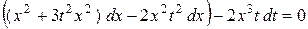 ,
,
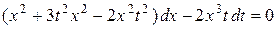 ,
,
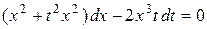 ,
,
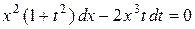 .
.
Теперь «разделим» переменные, разделив обе части уравнения на произведение 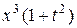 :
:
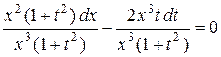 Þ
Þ 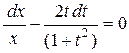 Þ
Þ 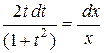
Проинтегрируем:
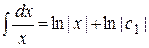 ,
, 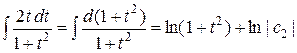 ,
,
получим 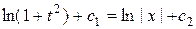 , или
, или
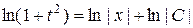 ,
,
где обозначили 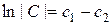 . Это сделано в целях упрощения дальнейших преобразований. Тогда
. Это сделано в целях упрощения дальнейших преобразований. Тогда
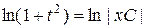 Þ
Þ 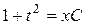 Þ
Þ 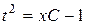 Þ
Þ 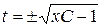 .
.
Возвращаясь к переменной у с помощью обратной замены 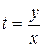 , получим
, получим
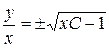 , или
, или 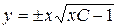
– общее решение исходного дифференциального уравнения.
Ответ: 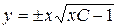 .
.
Пример 1. 5. Решить задачу Коши: 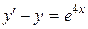 ,
, 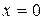 ,
, 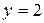 .
.
Решение
Сначала найдем общее решение данного уравнения.
Сравнивая форму записи этого уравнения с перечисленными в таблице 1, приходим к выводу, что это линейное дифференциальное уравнение первого порядка:
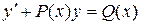 , где
, где 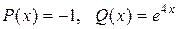 .
.
Решим его методом Бернулли. Положим 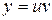 , где
, где 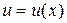 и
и 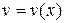 – новые неизвестные функции. Тогда
– новые неизвестные функции. Тогда 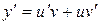 и заданное уравнение примет вид
и заданное уравнение примет вид
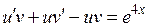 .
.
Преобразуем его: 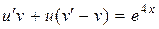 .
.
Теперь, согласно методу, чтобы найти функции и и v, нужно составить систему дифференциальных уравнений
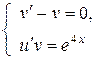
и последовательно найти сначала частное решение 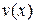 первого уравнения, а затем при найденной функции
первого уравнения, а затем при найденной функции 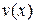 найти общее решение второго из этих уравнений. При этом отметим, что согласно методу, каждое из уравнений составленной системы является дифференциальным уравнением с разделяющимися переменными.
найти общее решение второго из этих уравнений. При этом отметим, что согласно методу, каждое из уравнений составленной системы является дифференциальным уравнением с разделяющимися переменными.
1) Решим уравнение 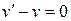 :
:
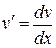 ,
, 
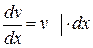 Þ
Þ 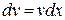 Þ
Þ 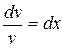 Þ
Þ
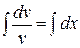 Þ
Þ 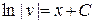 .
.
Согласно методу, достаточно найти какое-либо частное решение этого уравнения, поэтому положим, например, С = 0. Тогда
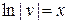 Þ
Þ 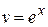 .
.
2) Теперь решим дифференциальное уравнение 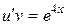 при
при 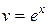 . Имеем
. Имеем
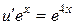 Þ
Þ 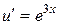 Þ
Þ 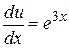 Þ
Þ 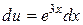 Þ
Þ 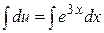 Þ
Þ
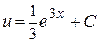 .
.
Тогда 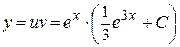 , или
, или 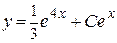 – это есть общее решение заданного дифференциального уравнения.
– это есть общее решение заданного дифференциального уравнения.
Теперь найдем частное решение исходного дифференциального уравнения, удовлетворяющее начальным условиям 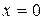 ,
, 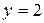 .
.
Подставив значения 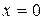 ,
, 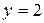 в общее решение
в общее решение 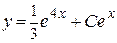 , найдем значение постоянной С:
, найдем значение постоянной С:
2 = 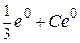 Þ
Þ 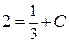 Þ
Þ 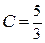 .
.
Тогда частное решение исходного дифференциального уравнения имеет вид:
у = 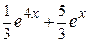 .
.
Ответ: у = 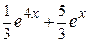 .
.
Пример 1.6.Решить уравнение 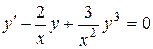 .
.
Решение
Область существования решения уравнения 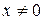 .
.
Запишем уравнение в виде 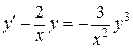 . Отсюда видно, что данное уравнение есть уравнение Бернулли:
. Отсюда видно, что данное уравнение есть уравнение Бернулли: 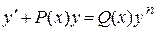 , где
, где 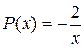 ,
, 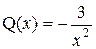 , п = 3 (см. таблицу 1, пункт 5).
, п = 3 (см. таблицу 1, пункт 5).
Для решения применим метод Бернулли: положим 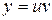 , где
, где 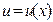 ,
, 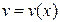 – новые неизвестные функции. Тогда
– новые неизвестные функции. Тогда 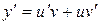 и заданное уравнение примет вид:
и заданное уравнение примет вид:
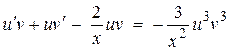 .
.
Преобразуем это уравнение:
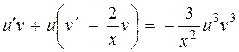 ,
,
составим систему дифференциальных уравнений 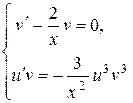
и последовательно решим уравнения этой системы.
1) Найдем частное решение дифференциального уравнения 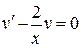 :
:
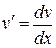 ,
, 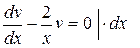 Þ
Þ 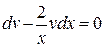 Þ
Þ
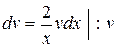 Þ
Þ 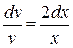 .
.
Интегрируем полученное дифференциальное уравнение с разделенными переменными:
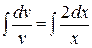 Þ
Þ 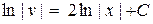 .
.
Положим 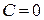 , тогда
, тогда 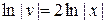 Þ
Þ 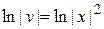 Þ
Þ 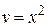 .
.
2) Решим дифференциальное уравнение 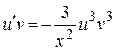 при
при 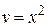 :
:
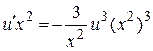 Þ
Þ 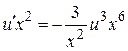 Þ
Þ
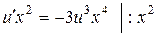 Þ
Þ 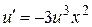 .
.
Это дифференциальное уравнение с разделяющимися переменными. «Разделяем» переменные и интегрируем:
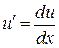 ,
, 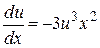 ½
½ 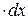 Þ
Þ 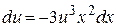 ï
ï 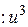 Þ
Þ 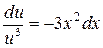 ;
;
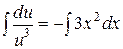 Þ
Þ 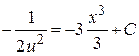 Þ
Þ 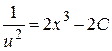 Þ
Þ
и = 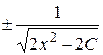 , или и =
, или и = 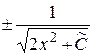 , где
, где 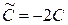 .
.
Тогда 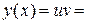
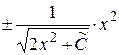 .
.
Таким образом, получили общее решение заданного дифференциального уравнения Бернулли: 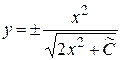 .
.
Ответ: 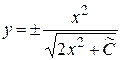 .
.
Пример 1.7.Найти интегральную кривую дифференциального уравнения 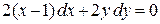 , проходящую через начало координат.
, проходящую через начало координат.
Решение:
Согласно условию задачи, требуется решить задачу Коши в ее геометрической постановке (стр. 14). Для этого, прежде всего, нужно найти общее решение дифференциального уравнения.
Заданное уравнение является дифференциальным уравнением с разделенными переменными. Следовательно, для того чтобы найти общее решение нужно проинтегрировать обе части уравнения:
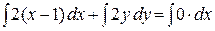 ,
,

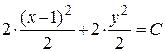 ,
,
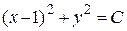 ,
, 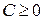 .
.
Получили общий интеграл заданного дифференциального уравнения. Заметим, что здесь постоянная С может принимать только неотрицательные значения, поскольку левая часть равенства 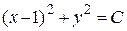 есть сумма квадратов.
есть сумма квадратов.
Общий интеграл 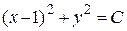 определяет семейство интегральных кривых, представляющих собой концентрические окружности радиуса
определяет семейство интегральных кривых, представляющих собой концентрические окружности радиуса 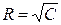 с центром в точке
с центром в точке 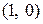 .
.
В нашем случае требуется найти одну интегральную кривую, проходящую через начало координат, т.е. через точку 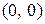 . Подставляя координаты этой точки в равенство
. Подставляя координаты этой точки в равенство 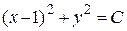 , найдем соответствующее значение постоянной С:
, найдем соответствующее значение постоянной С:
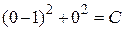 Þ
Þ 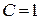 .
.
Таким образом, получили уравнение искомой интегральной кривой
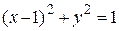 .
.
Еще раз следует подчеркнуть, это равенство можно рассматривать как частный интеграл заданного дифференциального уравнения, полученный из общего интеграла 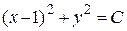 при конкретном значении постоянной
при конкретном значении постоянной 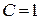 , а координаты точки О
, а координаты точки О 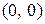 – начальные условия (
– начальные условия ( 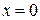 ,
, 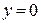 ), используемые для отыскания этого частного интеграла.
), используемые для отыскания этого частного интеграла.
Ответ: Окружность 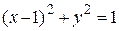 .
.
*) Вертикальная черта с записанным справа от нее выражением – такая символьная запись используется для того, чтобы показать, на какое число или выражение будут умножены (или разделены) обе части данного уравнения.
*) Как правило, в общем решении дифференциального уравнения принято записывать одну произвольную постоянную С независимо от того сколько интегралов приходится находить (количество постоянных равно порядку дифференциального уравнения).
*) Заметим, что рассмотренное дифференциальное уравнение имеет особые решения 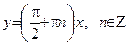 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Градиент функции, его свойства. | | |
Дата добавления: 2017-11-21; просмотров: 4824;










