Второй замечательный предел
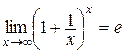 или в, общем, виде,
или в, общем, виде, 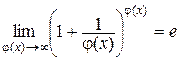 .
.
Также полезна следующая форма записи второго замечательного предела
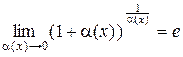
Второй замечательный предел используется для раскрытия неопределенности вида 1¥.
Рассмотрим примеры:
1) 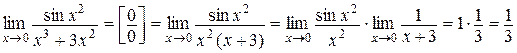 ;
;
2) 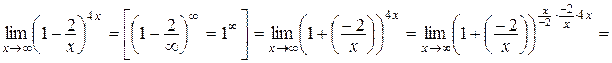
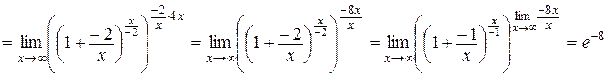 .
.
5. Сравнение бесконечно малых
Мы отмечали свойства бесконечно малых: алгебраическая сумма (конечного числа) бесконечно малых, произведение бесконечно малых есть бесконечно малая. О частном же бесконечно малых в этих свойствах ничего не говорилось. Оказывается, в зависимости от характера бесконечно малых, от скорости их стремления к нулю зависит и поведение их частного.
Рассмотрим, например, функции a(х) = х, b(х) = х2, g (х) = 2х + х2 , бесконечно малые при х® 0. Имеем:
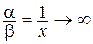 при х® 0,
при х® 0, 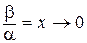 , а
, а 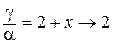 ,
,
т.е. частое может быть и сколь угодно большим, и бесконечно малым, и стремиться к конечному числу. При этом, заметим, что функция b(х) = х2 быстрее стремится к нулю, чем, например, a(х) = х:
| х | 0,1 | 0,01 | 0,001 |
| a(х)=х | 0,1 | 0,01 | 0,001 |
| b(х)=х2 | 0,01 | 0,0001 | 0,000001 |
Определение 2.11.
Пусть a(х) и b(х) – бесконечно малые в точке х0 функции.
1) Если 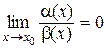 , то a(х) называется бесконечно малой более высокого порядка, чем b(х) и обозначается a = о(b).
, то a(х) называется бесконечно малой более высокого порядка, чем b(х) и обозначается a = о(b).
2) Если 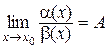 , 0 < |A| < ¥, то a(х) и b(х) – бесконечно малые одинакового порядка , обозначается a = О(b) или b = О(a).
, 0 < |A| < ¥, то a(х) и b(х) – бесконечно малые одинакового порядка , обозначается a = О(b) или b = О(a).
3) Если 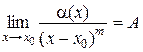 , 0 < |A| < ¥, то a(х) называется бесконечно малой порядка т в точке х0 (т ÎN). При этом функцию (х – х0)т называют эталоном бесконечно малых в точке х0.
, 0 < |A| < ¥, то a(х) называется бесконечно малой порядка т в точке х0 (т ÎN). При этом функцию (х – х0)т называют эталоном бесконечно малых в точке х0.
4) Если 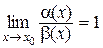 , то a(х) и b(х) называются эквивалентными (асимптотически равными). Обозначается a ~ b.
, то a(х) и b(х) называются эквивалентными (асимптотически равными). Обозначается a ~ b.
Справедлива
Теорема 2.9.
Пусть a(х) и b(х) – бесконечно малые в точке х0 функции.
1) Если a ~ b, то a – b = о(b), a – b = о(a), a ~ b ± о(a), a ± о(b)~b.
2) Если a = о(g), b = о(g), где g(х) – бесконечно малая в точке х0, то
a ± b = о(g), a ± о(b) = о(g).
3) Если a ~ a1 , b ~ b1 , где a1(х) и b1(х) – бесконечно малые в точке х0, то
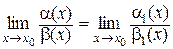
Доказательство:
1) Если a ~ b, то 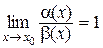 . Рассмотрим
. Рассмотрим
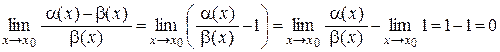 , а это и означает, что a – b = о(b). Аналогично можно показать, что a – b = о(a).
, а это и означает, что a – b = о(b). Аналогично можно показать, что a – b = о(a).
Рассмотрим
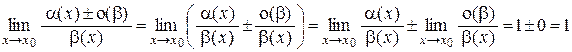 ,
,
откуда a ± о(b)~b. Утверждение a ~ b ± о(a) – доказать самостоятельно.
2) – доказать самостоятельно.
3) Учитывая a ~ a1 , b ~ b1, имеем
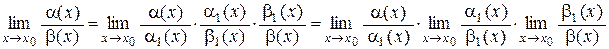 =
=
= 1 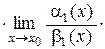 1 =
1 = 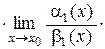 ЧТД.
ЧТД.
Замечание.
Как следует из теоремы 2.9, если a ~ b, то a = b + о(b). В этом случае, бесконечно малую b называют главной частью бесконечно малой a.
Справедливы следующие соотношения (таблица эквивалентности):
| при a® 0 | |
sin a ~ a
tg a ~ a
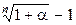 ~ ~ 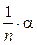
| arcsin a ~ a arctg a ~ a ln(1+a) ~ a ea - 1 ~ a |
Пользуясь этой таблицей и теоремой 2.9, можно вычислять сложные пределы:
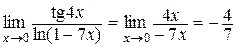 ,
,
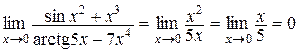 .
.
Аналогично можно определить сравнение бесконечно больших функций. Пусть f(x) и g(x) – бесконечно большие в точке х0 функции. Тогда
1) Если 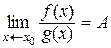 , 0 < |A| < ¥, то функции f(x) и g(x) – одинакового порядка роста. Обозначается f(x) = О(g(x)) или g(x) = О(f(x))
, 0 < |A| < ¥, то функции f(x) и g(x) – одинакового порядка роста. Обозначается f(x) = О(g(x)) или g(x) = О(f(x))
2) Если 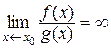 , то f(x) – более высокого порядка роста, чем g(x), а g(x) – более низкого порядка роста, чем f(x), обозначается
, то f(x) – более высокого порядка роста, чем g(x), а g(x) – более низкого порядка роста, чем f(x), обозначается
g(x) = о(f(x)).
3) Если 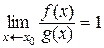 , то функции называются эквивалентными бесконечно большими. Обозначается f(x) ~ g(x).
, то функции называются эквивалентными бесконечно большими. Обозначается f(x) ~ g(x).
Свойства, сформулированные в теореме 2.9, могут быть перенесены и на эквивалентные бесконечно большие функции.
Дата добавления: 2017-11-21; просмотров: 668;










