ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ
Альтернативу методам, рассмотренным в предыдущем разделе, составляют итерационные методы. Какому типу методов отдать предпочтение в конкретной ситуации зависит от целого ряда обстоятельств таких, как характеристика используемых ЭВМ, вид уравнений, требуемая точность и т.д. Тем не менее определенно можно сказать, что для нахождения решения нелинейных СЛАУ использование итерационных методов является неизбежностью. Ниже рассмотрим ряд известных итерационных методов решения определенных СЛАУ.
6.1. МЕТОД ЯКОБИ
Рассмотрим СЛАУ вида
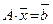 (1)
(1)
где
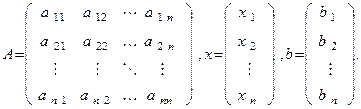
На этот раз не будем делать никаких предположений относительно матрицы A, за исключением того, что aii ¹ 0 i=1,2, ..., n, то есть диагональные элементы должны быть отличны от нуля. Выражаем в системе (1) x1 через первое уравнение этой системы, x2 через второе уравнение и т.д. В результате получим систему эквивалентную СЛАУ (1)
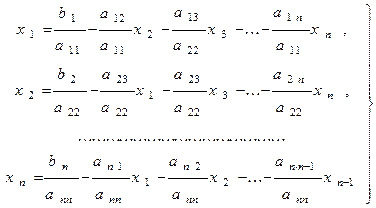 (2)
(2)
Решение системы (2) будем находить методом последовательных приближений. За нулевое (начальное) приближение к решению СЛАУ (1) выберем вектор x0 , равным столбцу свободных членов в системе (2), то есть  , и определим следующее приближение решений по формулам
, и определим следующее приближение решений по формулам
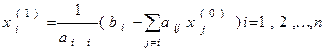 . (3)
. (3)
Полезно представить эти соотношения в матричной форме. Для этого положим
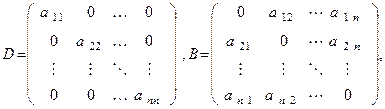
так что A= D-B. Тогда (3) можно переписать в виде
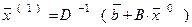 (4)
(4)
и всю последовательность Якоби определить как
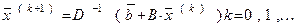 (5)
(5)
Итак, итерационный процесс Якоби (5) позволяет получить последовательность приближенных решений 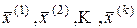 , которые должны удовлетворять условию
, которые должны удовлетворять условию
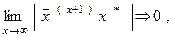
где через x* обозначено точное решение СЛАУ (1).
6.2. МЕТОД ГАУССА-ЗЕЙДЕЛЯ
Близкий итерационный процесс можно получить, если учесть следующее соображение. После того, как 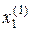 вычислено по формуле (4), его можно использовать при вычислении
вычислено по формуле (4), его можно использовать при вычислении 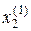 , а не первоначальное приближение
, а не первоначальное приближение 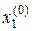 , которое имеет место в методе Якоби.
, которое имеет место в методе Якоби.
Если будем использовать новые значения сразу после их получения, то придем к формулам
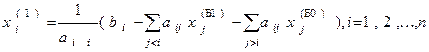 (6)
(6)
определяющих первый шаг итераций Гаусса-Зейделя. Чтобы представить эти итерации в матричной форме, введем верхнюю и нижнюю треугольные матрицы соотношениями

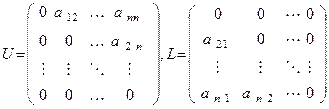 . (7)
. (7)
Если умножить i-е уравнение (6) на aii, то, как легко убедиться, n-е (6) можно переписать в виде
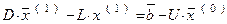 (8)
(8)
Матрица D-L не вырождена, поскольку она является нижней треугольной матрицей с отличными от нуля диагональными элементами. Следовательно, из (8) мы имеем
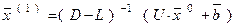
и всю последовательность итераций Гаусса-Зейделя можно определить так:
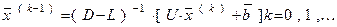 (9)
(9)
Запись итераций Якоби и Гаусса-Зейделя в виде (5) и (9) полезна для теоретических целей. При фактических вычисления обычно используют покомпонентные формулы (3) и (6).
6.3. ВОПРОСЫ СХОДИМОСТИ ИТЕРАЦИОННЫХ МЕТОДОВ РЕШЕНИЯ СЛАУ
Как метод Якоби, так и метод Гаусса-Зейделя представляет собой частичные случаи общего итерационного процесса
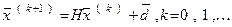 (10)
(10)
где задание матрицы H и вектора 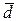 определяет конкретный метод. Так, в методе Якоби
определяет конкретный метод. Так, в методе Якоби 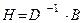 и
и 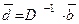 , в то время как в методе Гаусса-Зейделя
, в то время как в методе Гаусса-Зейделя 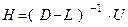 и
и 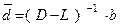 .
.
Предположим теперь, что 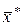 - точное решение системы
- точное решение системы 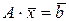 .
.
Тогда в методе Якоби мы имеем
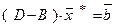 или
или 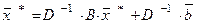 (11)
(11)
а в методе Гаусса-Зейделя
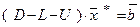 или
или 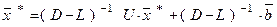 .
.  (12)
(12)
Так что в обоих случаях
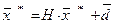 . (13)
. (13)
Если теперь вычесть (13) из (10), то получим
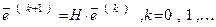 (14)
(14)
где 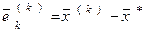 есть ошибка на
есть ошибка на 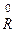 -ом шаге.
-ом шаге.
Уравнение (14) представляет собой основное соотношение, определяющее поведение погрешности приближенного решения в итерационных методах вида (10). Отметим, что векторы 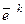 будут стремиться к нулю при
будут стремиться к нулю при 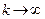 в том случае, если спектральный радиус
в том случае, если спектральный радиус 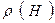 матрицы H меньше единицы. Сформулируем этот основной результат для итерационного процесса (10).
матрицы H меньше единицы. Сформулируем этот основной результат для итерационного процесса (10).
ТЕОРЕМА 6. Итерации (10) сходятся к решению x* при любом начальном приближении x0 в том и только в том случае, если r(H)<1 (то есть спектральный радиус итерационной матрицы меньше единицы). Эта теорема не ограничивается методами Якоби и Гаусса-Зейделя. Она применима к любому итерационному процессу вида (10) при условии, что вектор 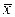 * удовлетворяет уравнению (13) , и является основным теоретическим результатом для итерационных методов. Согласно этой теореме для того, чтобы исследовать сходимость конкретного итерационного метода, мы должны определить, меньше ли единицы спектральный радиус итерационной матрицы этого метода. В общем случае это очень сложная проблема, решение которой может потребовать вычисления всех собственных значений итерационной матрицы. Однако для некоторых итерационных методов и для некоторых классов матриц удается сравнительно просто показать, что критерии сходимости выполняются.
* удовлетворяет уравнению (13) , и является основным теоретическим результатом для итерационных методов. Согласно этой теореме для того, чтобы исследовать сходимость конкретного итерационного метода, мы должны определить, меньше ли единицы спектральный радиус итерационной матрицы этого метода. В общем случае это очень сложная проблема, решение которой может потребовать вычисления всех собственных значений итерационной матрицы. Однако для некоторых итерационных методов и для некоторых классов матриц удается сравнительно просто показать, что критерии сходимости выполняются.
Ниже приведем несколько таких примеров для методов Якоби и Гаусса-Зейделя.
ТЕОРЕМА 7. Предположим, что матрица A строго диагонально доминирующая, то есть
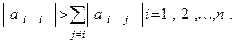 (15)
(15)
Тогда итерации Якоби и итерации Гаусса-Зейделя сходятся к единственному решению уравнения 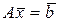 при любом начальном приближении x0.
при любом начальном приближении x0.
Для метода Якоби эта теорема доказывается очень просто. Так как H=D-1×B , то из (15) сразу следует, что сумма абсолютных величин элементов каждой строки H меньше единицы, то есть½½H½½<1.
4. РЕШЕНИЕ НЕОДНОРОДНОЙ СЛАУ ИЗ m УРАВНЕНИЙ
С n НЕИЗВЕСТНЫМИ
Пусть дана система m линейных алгебраических уравнений с n неизвестными (1). Пусть ranqA= ranq 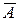 , то есть система совместна. Не ограничиваясь общностью, будем считать, что базисный минор располагается в первых
, то есть система совместна. Не ограничиваясь общностью, будем считать, что базисный минор располагается в первых 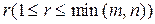 строках и столбцах матрицы A. Отбросив последние m-r уравнений системы (1), запишем укороченную систему
строках и столбцах матрицы A. Отбросив последние m-r уравнений системы (1), запишем укороченную систему
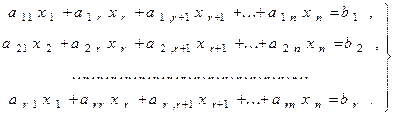 (2)
(2)
которая эквивалентна исходной.
Назовем неизвестные x1 ,x2 , ..., xr базисными, а xr+1 , ..., xn- свободными. Перенесем слагаемыe, содержащие свободные неизвестные, в правую часть уравнения (2). В результате, получим систему линейных алгебраических уравнений относительно базисных неизвестных
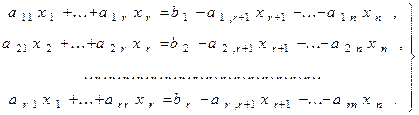 (3)
(3)
которая для каждого набора значений свободных неизвестных xr+1= c1, xr+2= c2, ..., xn=cn-r. имеет единственное решение: x1= f1,(c1, c2 , ..., cn-r), x2= f2,(c1, c2 , ..., cn-r), ..., xr= fr,(c1, c2 , ..., cn-r). Решение системы (3) можно определить либо по методу Крамера, либо методом Гаусса.
Общее решение СЛАУ можно записать в виде матрицы-столбца следующим образом:
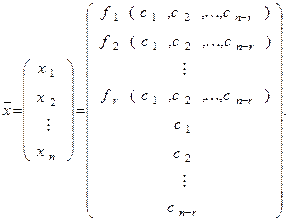 (4)
(4)
Дата добавления: 2016-06-05; просмотров: 2144;










