Сходимость знакопеременных рядов.
Рассмотрим ряды, члены которых имеют произвольные знаки, такие ряды будем называть знакопеременными(заметим, что в математической литературе термины знакопеременный и знакочередующийся ряд – о таких рядах речь пойдет позже – означают одно и то же; но мы здесь приняли терминологию, используемую Пискуновым Н.С. в его «Дифференциальном и интегральном исчислении» только для сокращения записи: вместо слов «ряд, члены которого имеют произвольные знаки» будем говорить «знакопеременные ряды»). Если заданный ряд имеет только конечное число отрицательных членов, то, отбросив их, можно свести дело к исследованию ряда с положительными членами. То же касается ряда, в котором только конечное число положительных членов. Поэтому будем заведомо предполагать, что среди членов ряда есть бесконечное количество как положительных, так и отрицательных членов.
Справедлива следующая теорема
Теорема 30. 8.(признак абсолютной сходимости)
Пусть дан ряд 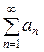 с членами произвольных знаков. Если сходится ряд
с членами произвольных знаков. Если сходится ряд
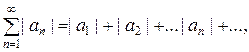
составленный из абсолютных величин его членов, то сходится и данный ряд. При этом 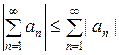 .
.
Определение 30.4.Если ряд 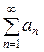 сходится и сходится ряд
сходится и сходится ряд 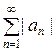 , то ряд
, то ряд 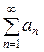 называется абсолютно сходящимся. Если ряд
называется абсолютно сходящимся. Если ряд 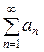 сходится, а ряд
сходится, а ряд 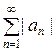 расходится, то ряд
расходится, то ряд 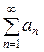 называется условно (не абсолютно) сходящимся.
называется условно (не абсолютно) сходящимся.
Для выяснения абсолютной сходимости заданного ряда к ряду из его модулей могут быть применены признаки, рассмотренные нами в предыдущем пункте. Но нужно быть осторожным с признаками расходимости: если ряд из модулей расходится, то исходный ряд может и сходиться (условно). Исключение составляют лишь признак Даламбера и радикальный признак Коши, так как когда эти признаки констатируют расходимость ряда 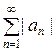 , то это означает, что
, то это означает, что 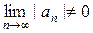 , но тогда и
, но тогда и 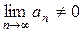 , что означает расходимость ряда
, что означает расходимость ряда 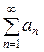 .
.
Сформулируем эти признаки применительно к знакопеременному ряду
Признак Даламбера. Если для знакопеременного ряда 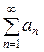 существует
существует 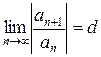 , то
, то
при d < 1 ряд сходится абсолютно,
при d > 1 ряд расходится,
при d =1 нужны дополнительные исследования.
Признак Коши радикальный. Если для знакопеременного ряда 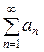 существует
существует 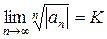 , то
, то
при K < 1 ряд сходится абсолютно,
при K > 1 ряд расходится,
при K = 1 требуются дополнительные исследования
Пример. Исследуем сходимость ряда 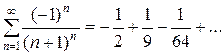 . Применим к нему признак Коши:
. Применим к нему признак Коши: 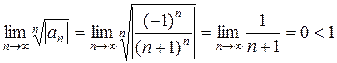 – ряд сходится абсолютно.
– ряд сходится абсолютно.
Среди знакопеременных рядов особую роль играют так называемые знакочередующиеся ряды. Знакочередующимся рядом называют ряд, члены которого поочередно имеют то положительный, то отрицательный знаки (см предыдущий пример). Такой ряд обычно записывают в виде
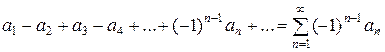 ,
,
при этом предполагается, то все ап > 0.
Для знакочередующихся рядов имеет место
Теорема 30.9. (Теорема Лейбница)
Если члены знакочередующегося ряда 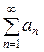 убывают по абсолютной величине, т.е."п | an| >| an+1|, и
убывают по абсолютной величине, т.е."п | an| >| an+1|, и 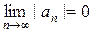 , то ряд сходится. При этом сумма ряда по абсолютной величине не превосходит модуля первого члена ряда, т.е.
, то ряд сходится. При этом сумма ряда по абсолютной величине не превосходит модуля первого члена ряда, т.е. 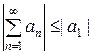 и имеет тот же знак, что и первый член ряда .
и имеет тот же знак, что и первый член ряда .
Ряд, удовлетворяющий условиям теоремы Лейбница, называют рядом лейбницевского типа.
Пример. Рассмотрим сходимость ряда 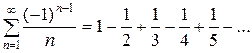 . Проверим выполнение условий Теоремы 5.9.: | an| >| an+1|, действительно,
. Проверим выполнение условий Теоремы 5.9.: | an| >| an+1|, действительно, 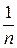 >
> 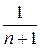 "п ³1, а также
"п ³1, а также 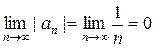 , значит, ряд
, значит, ряд 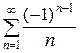 сходится. А так как ряд из абсолютных величин этого ряда есть расходящийся гармонический ряд
сходится. А так как ряд из абсолютных величин этого ряда есть расходящийся гармонический ряд 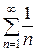 , то исходный ряд сходится условно.
, то исходный ряд сходится условно.
Замечание. Так как любой остаток ряда лейбницевского типа есть также ряд лейбницевского типа, то в случае сходимости ряда, остаток ряда по абсолютной величине не превосходит модуля своего первого члена:
| Rn | = |S – Sn| £ |an+1|.
Это удобно использовать для оценки точности приближенного вычисления суммы данного ряда.
Например, если требуется найти сумму ряда с точность e, то достаточно найти такой член ряда, который по абсолютной величине меньше e, т.е. |an+1| <e, тогда искомое значение суммы ряда будет равно сумме всех членов ряда, предшествующих найденному члену. Или, наоборот, взяв значение п-ой частичной суммы за приближенное значение суммы ряда, можно, оценив первый член остатка ряда, сказать, с какой точностью эти вычисления произведены.
Например, 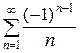 »
» 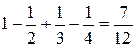 с точностью до 0,2.
с точностью до 0,2.
К приведенным ранее свойствам числовых рядов необходимо добавить следующие важные свойства:
Свойство 4. Если ряд 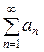 абсолютно сходится, то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму, что и исходный ряд.
абсолютно сходится, то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму, что и исходный ряд.
Если ряд 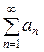 условно сходится , то каким бы ни было число А ( конечным или бесконечным), можно так переставить члены в этом ряде, что сумма полученного ряда будет равна А.
условно сходится , то каким бы ни было число А ( конечным или бесконечным), можно так переставить члены в этом ряде, что сумма полученного ряда будет равна А.
Иначе говоря, абсолютно сходящиеся ряды (и знакопостоянные в том числе) обладают переместительным свойством, а для условно сходящихся рядов от перемены мест слагаемых сумма меняется!
Например, можно доказать, что
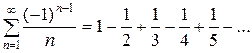 = ln2.
= ln2.
Переместив его члены, можно получить:
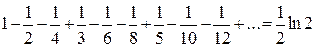 ,
, 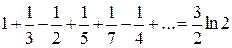 ,
,
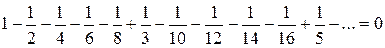 и т.п.
и т.п.
Дата добавления: 2017-11-21; просмотров: 1631;










