Сложение когерентных волн
Если же разность фаз d постоянна во времени, то такие колебания (и волны) называют когерентными. В случае суперпозиции когерентных волн, интенсивность результирующего колебания определяется (см.4.8)
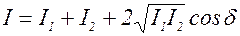 (4.11)
(4.11)
Последнее слагаемое в формуле (4.11) называют интерференционным членом. Рассмотрим его влияние на результирующую интенсивность.
В точках пространства, где 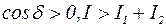 ; там же, где
; там же, где 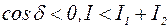 . Другими словами, при суперпозиции когерентных волн происходит перераспределение интенсивности света I в пространстве: в одних местах возникают максимумы, в других - минимумы интенсивности. Это явление называется интерференцией волн. Особенно отчетливо (контрастно) интерференция проявляется тогда, когда
. Другими словами, при суперпозиции когерентных волн происходит перераспределение интенсивности света I в пространстве: в одних местах возникают максимумы, в других - минимумы интенсивности. Это явление называется интерференцией волн. Особенно отчетливо (контрастно) интерференция проявляется тогда, когда 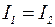 . Тогда, согласно (4.11),
. Тогда, согласно (4.11), 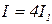 в максимумах и
в максимумах и 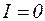 в минимумах. Для некогерентных волн при равенстве
в минимумах. Для некогерентных волн при равенстве 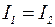 интенсивность
интенсивность 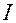 всюду одинакова и, согласно (4.10),
всюду одинакова и, согласно (4.10), 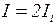 .
. 
Итак, чтобы наблюдалось перераспределение интенсивности при наложении световых волн должно выполниться три основных условия:
1) частоты их одинаковы,
2) направления электрических векторов совпадают,
3) разность фаз d складываемых колебаний не должна меняться во времени.
Это условия когерентности складываемых волн.
Из условия (4,11) можно сформулировать фазовые условия максимумов и минимумов:
1) если 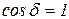 , то выполняется условие
, то выполняется условие 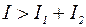 ,т.е. выполняется условие максимума. В этом случае разность фаз должна удовлетворять условию
,т.е. выполняется условие максимума. В этом случае разность фаз должна удовлетворять условию 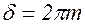 , где m=0,1,2, и т.д. и называется порядковым числом максимумов.
, где m=0,1,2, и т.д. и называется порядковым числом максимумов.
2) если 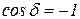 , то выполняется условие
, то выполняется условие 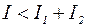 ,т.е. выполняется условие минимума. В этом случае разность фаз должна удовлетворять условию
,т.е. выполняется условие минимума. В этом случае разность фаз должна удовлетворять условию 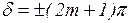 , где m=0.1,2, и т.д..
, где m=0.1,2, и т.д..
Дата добавления: 2017-10-04; просмотров: 3807;











