эллипсоид инерции, главные оси
Выбираем систему декартовых координат с началом в центре О.Проведем через начало координат произвольную ось Оl, образующую с осями координат Ох, Оу и Оz соответственно углы 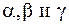 (рис. 28).
(рис. 28).
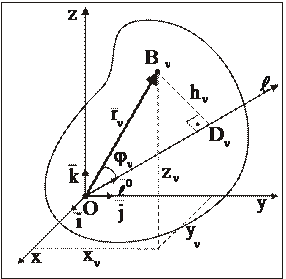
Рис. 28
На основании соотношения (3.8) для момента инерции СМТ относительно оси Ol имеем:
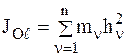 . (3.23)
. (3.23)
Для прямоугольного треугольника ODnBn можно записать
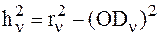 , (3.24)
, (3.24)
где 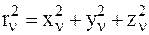 ,
,
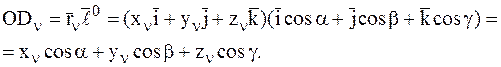 (3.25)
(3.25)
Здесь 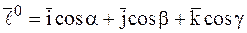 – единичный вектор оси Оl.
– единичный вектор оси Оl.
Преобразуем соотношение (3.24), с учетом формулы (3.25) и соотношения 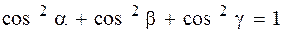 , следующим образом:
, следующим образом:
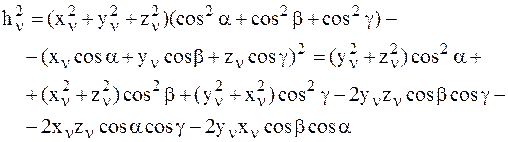 (3.26)
(3.26)
Подставим соотношение (3.26) в соотношение (3.23):
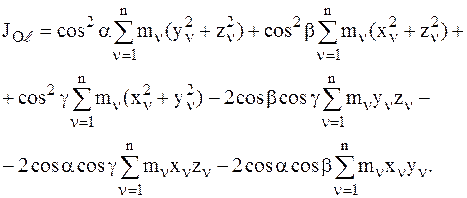 (3.27)
(3.27)
Учтем, что на основании соотношений (3.14) можно записать:
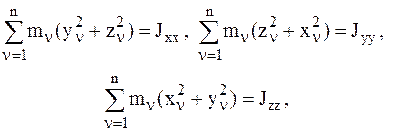 (3.28)
(3.28)
где Jxx, Jyy, Jzz – моменты инерции СМТ относительно координатных осей. Величины
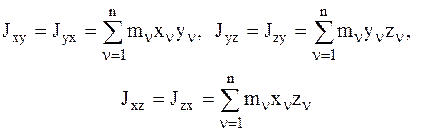 (3.29)
(3.29)
называются произведениями инерции или центробежными моментами инерции СМТ.
С учетом (3.28) и (3.29) соотношение (3.27) примет вид:
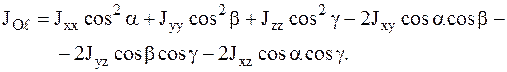 (3.30)
(3.30)
Из равенства (3.30) следует, что для определения момента инерции СМТ относительно любой оси, проходящей через начало координат О, достаточно знать шесть величин Jxx, Jyy, Jzz, Jxy, Jyz, Jxz и направление этой оси, определяемое косинусами углов a, b, g. Шесть величин Jxx, Jyy, Jzz, Jxy, Jyz, Jxz зависят от положения точки О и от направления координатных осей, так как с их изменением изменяются xn, yn, zn. Указанные величины можно расположить в виде симметричной матрицы:
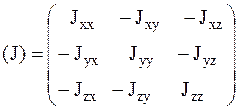 , (3.31)
, (3.31)
которая называется тензором инерции, элементы этой матрицы называются компонентами тензора инерции.
Для характеристики распределения моментов инерции СМТ относительно различных осей, проходящих через заданную точку, используется поверхность второго порядка – эллипсоид инерции. Для построения этой поверхности на каждой осиl, проходящей через точку  , откладывается вектор
, откладывается вектор  , модуль которого равен:
, модуль которого равен:
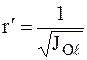 . (3.32)
. (3.32)
Выразим косинусы углов 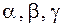 через координаты
через координаты 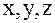 вектора
вектора 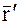 :
:
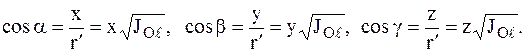 (3.33)
(3.33)
Подставив в соотношение (3.30) формулы (3.33), получим уравнение поверхности второго порядка:
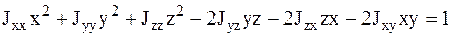 . (3.34)
. (3.34)
Геометрическое место концов вектора 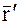 располагается на поверхности, которая называется эллипсоидом инерции. Для каждой точки O имеется свой эллипсоид инерции. Эллипсоид инерции для центра масс СМТ называется центральным эллипсоидом инерции. Оси эллипсоида инерции называются главными осями инерции. В общем случае эллипсоид инерции имеет три взаимно перпендикулярные главные оси инерции. Они являются его осями инерции.
располагается на поверхности, которая называется эллипсоидом инерции. Для каждой точки O имеется свой эллипсоид инерции. Эллипсоид инерции для центра масс СМТ называется центральным эллипсоидом инерции. Оси эллипсоида инерции называются главными осями инерции. В общем случае эллипсоид инерции имеет три взаимно перпендикулярные главные оси инерции. Они являются его осями инерции.
Моменты инерции относительно главных осей инерции называются главными моментами инерции, а относительно главных центральных осей инерции – главными центральными моментами инерции.
Если уравнение эллипсоида инерции отнести к его главным осям Ox', Oy', Oz', то оно примет вид:
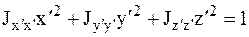 , (3.35)
, (3.35)
где x', y', z'– текущие координаты точки, расположенной на эллипсоиде инерции, относительно главных осей инерции; 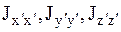 – главные моменты инерции.
– главные моменты инерции.
Центробежные моменты инерции относительно главных осей инерции равны нулю
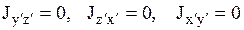 .
.
Дата добавления: 2016-06-05; просмотров: 3021;










