Устойчивость ЛИС-цепей

Обычно к ЛИС-цепям предъявляется требование устойчивости. Напомним, что линейная цепь называется устойчивой, если отклик на воздействие, ограниченное по модулю, также ограничен.

Для устойчивости ЛИС-цепи необходимо и достаточно, чтобы ее импульсная характеристика была абсолютно суммируемой, т.е. выполнялось условие [7]

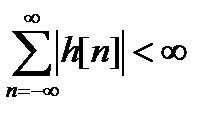. (12.13)

Очевидно, для импульсных характеристик конечной длины это условие выполняется всегда, поэтому КИХ-цепи всегда устойчивы.

Рекурсивные цепи могут быть неустойчивыми из-за наличия обратных связей. Анализ устойчивости ЛИС-цепей основан на использовании z-преобразования, которое формально может быть получено из преобразования Фурье заменой величины e^jω на комплексное переменное z:

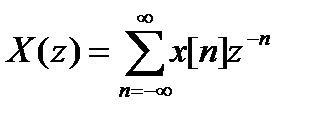. (12.14)

z-преобразование может сходиться для одних значений комплексного переменного z и расходиться для других. Множество точек комплексной z-плоскости, в которых z-преобразование сходится, называется областью сходимости. Для абсолютно суммируемой импульсной характеристики область сходимости ее z-преобразования содержит единичную окружность. Если цепь является физически реализуемой (каузальной), то она устойчива в том и только в том случае, если все полюсы ее передаточной функции

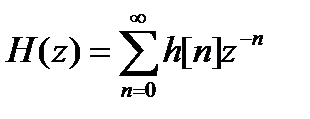
по модулю меньше единицы, т.е. находятся внутри единичной окружности.

Самый широкий класс ЛИС-цепей конечного порядка образуют цепи, структура которых может быть сведена к каскадному соединению трансверсальной и рекурсивной частей, что соответствует разностному уравнению вида

y[n] = b₀x[n] + b₁x[n - 1] + b₂x[n - 2] + … + b_N-1x[n - N + 1] +

+ α₁y[n - 1] + α₂y[n - 2] + … + α_M-1x[n - M + 1] =

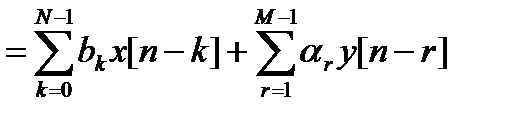, (12.15)

откуда следует выражение для КЧХ дробно-рационального вида

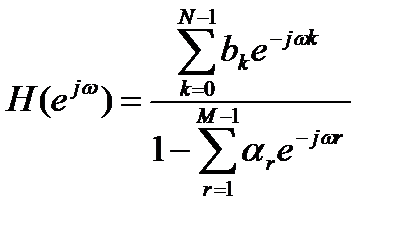. (12.16)

В общем случае ЛИС-цепь конечного порядка с КЧХ вида (12.16) имеет бесконечно длинную импульсную характеристику (БИХ), но если полином-числитель делится на знаменатель без остатка, то результатом деления оказывается полином и импульсная характеристика имеет конечную длину (таковы, например, КИХ-фильтры на основе частотной выборки, см. далее).

ЦИФРОВЫЕ ФИЛЬТРЫ

Дискретное преобразование Фурье представляет собой не только инструмент анализа, но и алгоритм ЦОС. На его основе фильтрация сигналов в частотной области может быть реализована следующим образом: для входного сигнала вычисляется ДПФ, полученные спектральные отсчеты умножаются на КЧХ фильтра, а результат умножения подвергается обратному ДПФ. Этот метод фильтрации более экономичный, чем вычисление свертки входного сигнала с импульсной характеристикой фильтра, благодаря существованию очень эффективных (быстрых) алгоритмов, которые получили название быстрого преобразования Фурье (БПФ).

Основное назначение дискретных ЛИС-цепей заключается в фильтрации дискретных сигналов, т.е. в избирательном воздействии на амплитуды и начальные фазы гармонических составляющих различных частот. Это фактически означает, что любая ЛИС-цепь представляет собой фильтр. Однако интерес представляет построение фильтров с заданными частотно-избирательными и фазовыми свойствами. Построить (синтезировать) фильтр – значит найти его разностное уравнение (т.е. алгоритм вычисления выходного сигнала по известному входному) и/или структурную схему.

Таким образом, под синтезом цифрового фильтра (ЦФ) обычно понимается построение дискретной ЛИС-цепи с КЧХ заданной формы. При решении задачи синтеза обычно не делают различия между дискретными и цифровым цепями, хотя, строго говоря, дискретная ЛИС-цепь становится цифровой в результате квантования коэффициентов ее разностного уравнения.

Ранее было показано, что ЛИС-цепь конечного порядка имеет в общем случае КЧХ дробно-рационального вида (12.7), поэтому, очевидно, задача синтеза ЦФ сводится к аппроксимации желаемой КЧХ функцией дробно-рационального вида, так как, зная эту функцию, легко составить структурную схему цепи или записать разностное уравнение вида (12.6). Указанная аппроксимация сравнительно легко выполняется для КИХ-цепей, когда дробнорациональная функция вырождается в полином, и представляет собой непростую задачу для общего случая. Поэтому методы синтеза ЦФ с конечными и бесконечными импульсными характеристиками различаются.