Цепи с конечной импульсной характеристикой (КИХ-цепи)

Предположим, что импульсная характеристика некоторой цепи h[n] имеет конечную длину N, т.е. h[n] ≠ 0, 0 ≤ n ≤ N - 1. Тогда свертка (12.10) принимает вид конечной суммы

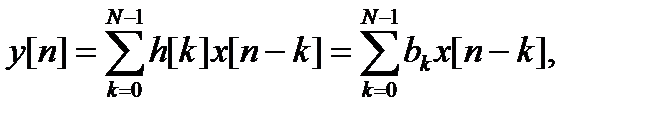
и может быть записана в виде разностного уравнения

y[n] = b₀x[n] + b₁x[n - 1] + b₂x[n - 2] + … + b_{N -1}x[n - N + 1]. (12.12)

Вычисление каждого значения выходного сигнала требует учета текущего и N - 1 предшествующих отсчетов входного сигнала и может быть выполнено цепью, структурная схема которой показана на рис. 12.3. Такие цепи называются трансверсальными, или цепями с конечной импульсной характеристикой (КИХ-цепями).

Комплексная частотная характеристика КИХ-цепи имеет вид полинома порядка N - 1 относительно e^-jω:

.

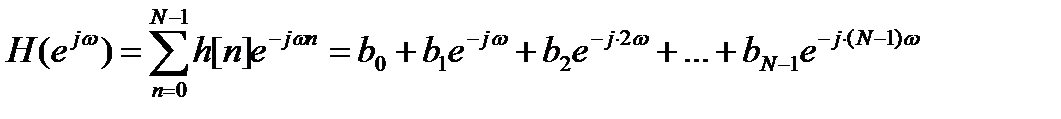Таким образом, КИХ-цепь умножает спектральную плотность входной последовательности на полином.

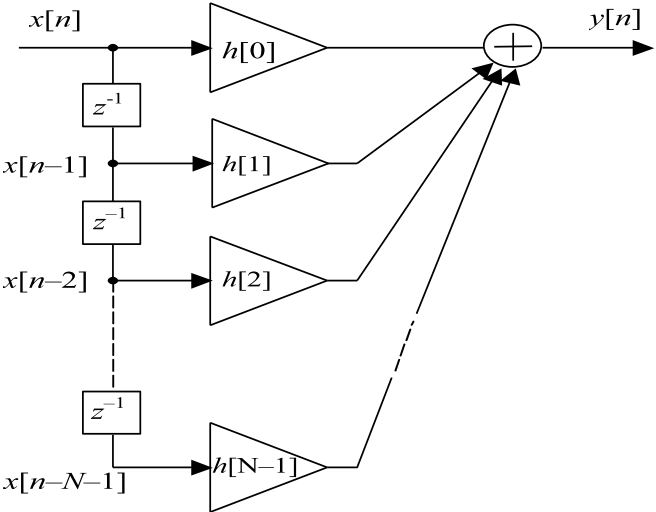
Рис. 12.3. Структура цепи с конечной импульсной характеристикой

Рекурсивные цепи

Другой важный для практики класс дискретных ЛИС-цепей составляют цепи, которые не умножают, а делят спектральную плотность входной последовательности на полином некоторого порядка M - 1 относительно e^-jω. Обозначим этот полином A(e^jω) = α₀ + α₁e^-jω + α₂e^-j∙2ω + … + α_M-1e^-j∙(M-1)ω, тогда спектральные плотности входной и выходной последовательностей связаны выражением Y(e^jω) = X(e^jω) / A(e^jω), следовательно, X(e^jω) = Y(e^jω) A(e^jω), откуда по аналогии с (12.3) можно записать

x[n] = α₀y[n] + α₁y[n - 1] + α₂y[n - 2] + … + α_M-1y[n - M + 1].

Решая это уравнение относительно выходного сигнала, получаем

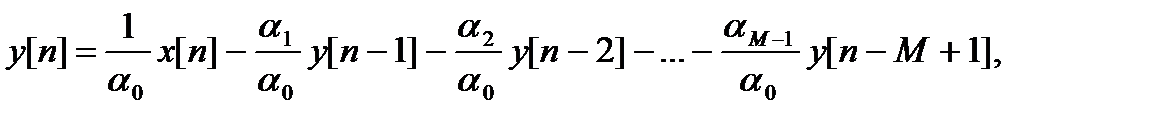
откуда, вводя обозначения b = 1/α₀, α_i = -α_i/α₀, находим окончательно разностное уравнение рекурсивной цепи

y[n] = bx[n] + α₁y[n - 1] + α₂y[n - 2] + … + α_M-1y[n - M + 1],

структура которой показана на рис. 12.4.

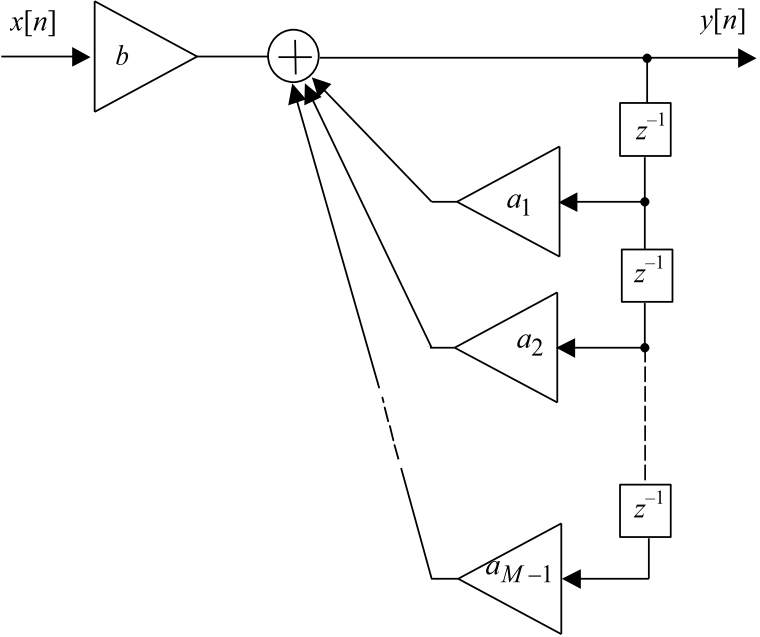
Рис. 12.4. Структура рекурсивной цепи