Рассмотрим однородные уравнения

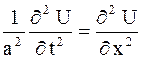
(2.78)

,

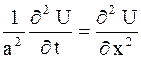(2.79)

для которых граничные условия имеют вид

.

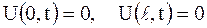(2.80)

а начальные условия таковы

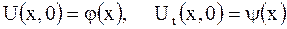
(2.81)

для (2.78)

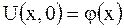
(2.82)

для (2.79).

Процесс решения разбивается на два этапа: I – нахождение частных решений; II – нахождение общего решения и удовлетворение начальным условиям.

I. Ищутся всевозможные частные решения (2.78) в виде

.

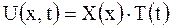(2.83)

В результате подстановки функции такого вида в уравнение (2.78) получаем

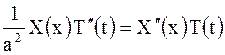или .

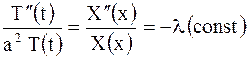Последнее уравнение распадается на два обыкновенных дифференциальных уравнения относительно функци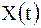й и :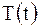

.

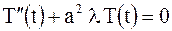(2.84)

.

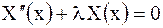(2.85)

Как говорят, в уравнении (2.78) переменные разделены.

Подставляя (2.83) в граничные условия (2.80), получим

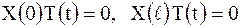, откуда

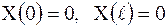
(2.86)

(т.к. случай 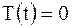не представляет интереса, поскольку тогда ).

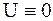Для определения функции 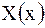получена з а д а ч а Ш т у р м а - Л и у в и л л я: найти такие значения параметра 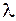, при которых существуют нетривиальные решения уравнения (2.85), удовлетворяющие граничным условиям (2.86). Те значения параметра 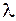, для которых задача (2.85) – (2.86) имеет нетривиальные решения, называются собственными значениями, а сами решения – собственными функциями. Нетривиальные решения задачи (2.85) – (2.86) возможны лишь при значениях

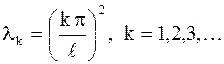
Этим значениям 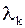соответствуют собственные функции

.

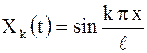При 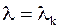общее решение уравнения (2.84) имеет вид

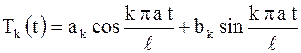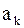, где и 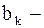произвольные постоянные.

Таким образом, произведения функци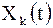й и 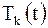образуют частные решения уравнения (2.78), удовлетворяющие краевым условиям (2.80)

.

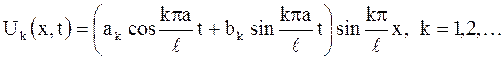II. При помощи собственных функций строится общее решение уравнения в частных производных, которое в силу свойства линейного однородного уравнения можно взять в виде комбинации полученных частных решений - ряда

.

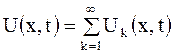(2.87)

Для уравнения (2.78) общее решение имеет вид

.

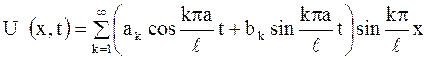(2.88)

Подставляя решение (2.88) в начальные условия (2.81), определяют значения коэффициентов 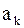и 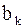, пользуясь разложением функци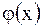й и 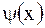в ряд Фурье (в ряд по системе собственных функций 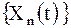). В результате имеем

, .

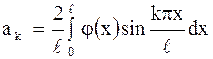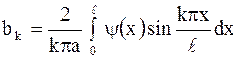(2.89)

Решение уравнения теплопроводности (2.79) получается применением этой же схемы с той лишь разницей, что вместо уравнения (2.84) надо решать уравнение

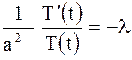или ,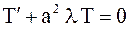

общее решение которого есть

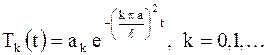
где 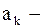произвольные постоянные.

Следовательно, 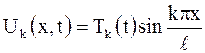и общее решение (2.87) принимает вид

.

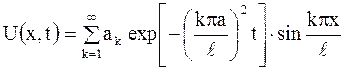(2.90)

Потребовав выполнения начального условия (2.82), коэффициенты 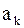будут найдены как коэффициенты разложения функции 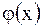в ряд Фурье:

.

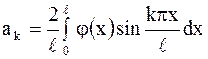(2.91)

Приведенные здесь решения для линейных однородных уравнений с однородными граничными условиями будут использованы также при рассмотрении неоднородных и однородных уравнений с однородными и неоднородными граничными условиями как составные части решений краевых задач.