Последовательность решения задач

1. Заданная линия заключается во вспомогательную плоскость-посредник.

2. Строится линия пересечения заданного Г.О. со вспомогательной плоскостью.

3. Строится недостающая проекция этой линии пересечения.

4. Определяются точки пересечения заданного Г.О. и построенной линии пересечения.

5. Определяется видимость Г.О.

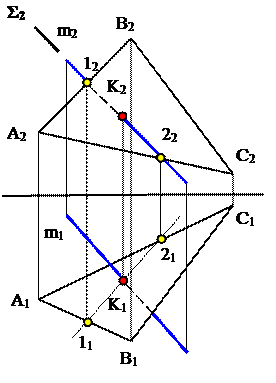
Задача 6: Построить точку пересечения прямой m с плоскостью α (ΔАВС) (рис. 6).

Дано: Решение:

Рис. 6

Последовательность построения

1. Через проекцию прямой m₂ провести вспомогательную фронтально-проецирующую плоскость – посредник Σ₂.

2. Плоскость Σ₂ пересекает фронтальную проекцию ΔАВС по прямой 1₂2₂.

3. Строится горизонтальная проекция прямой 1₁2₁.

4. Линия m₁ пересекается с прямой 1₁2₁ в точке К₁.

5. Строится фронтальная проекция точки К₂.

6. Определяется видимость геометрических образов.

Для того, чтобы определить видимость геометрических образов, необходимо установить какая точка, изображенная на чертеже выше в пространстве, а какая ниже.

Определение высоты точек на чертеже:

На горизонтальной плоскости П₁, ближе к наблюдателю та точка, фронтальная проекция которой дальше от оси Х.

На фронтальной плоскости П₂ выше та точка, горизонтальная проекция которой дальше от оси Х.

Задача 7: Построить линию пересечения плоскостей ΔАВС и ΔDEF (рис. 7, 8)

Дано:

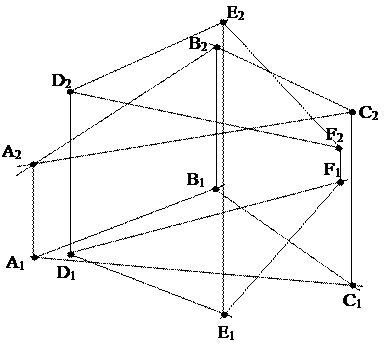Рис.7

Решение:

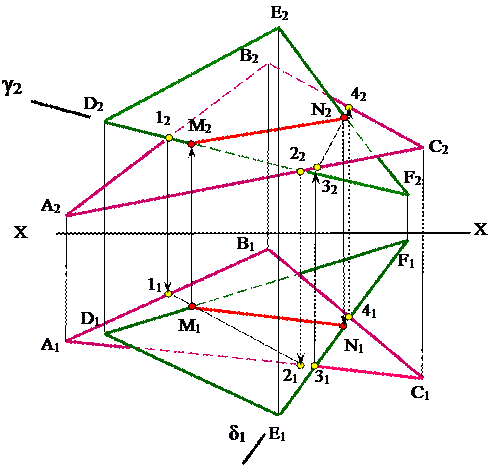
Рис. 8

Последовательность построения

1. Линия D₂F₂ заключается в вспомогательную плоскость-посредник γ₂,

плоскость γ₂перпендикулярна П₂.

2. Плоскость γ₂пересекается с фронтальной проекцией ΔАВСпо линии 1₂2₂

(γ₂ ∩ β₂ = 1₂2₂).

3. Построить горизонтальную проекцию линии пересечения 1₁2₁.

4. Линия 1₁2₁ пересекается с линиейD₁F₁ в точке М₂ (1₁2₁∩D₁F₁= М₂).

5. Построить горизонтальную проекцию точки М₁.

6. Линия Е₁F₁ заключается в вспомогательную плоскость-посредник δ₁,

плоскостьδ₁перпендикулярна П₁.

7. Плоскостьδ₁пересекается с горизонтальной проекцией ΔАВСпо линии 3₁4₁ (δ₁∩ β₁= 3₁4₁).

8. Построить фронтальную проекцию линии пересечения 3₂4₂.

9. Линия 3₂4₂ пересекается с линиейЕ₂F₂ в точке N₂ (3₂4₂ ∩ Е₂F₂ = N₂).

10. Построить горизонтальную проекцию точки N₁.

11. Соединить одноименные проекции точек М₂N₂, М₁N₁.

12. Определить видимость линий на чертеже.

Задача 8: Построить точки пересечения наклонной пирамиды с прямой общего положения m (рис.9).

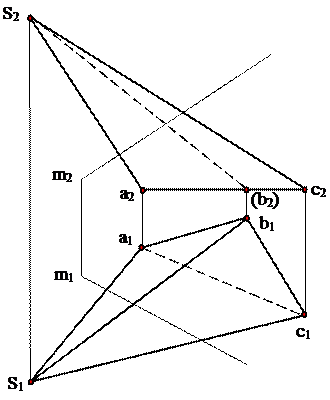
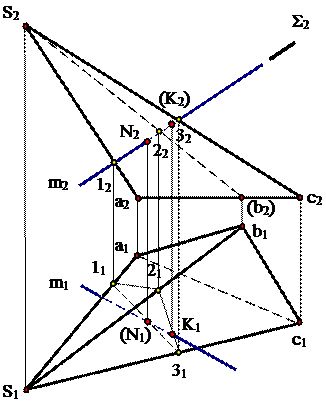Дано: Решение:

Рис.9

Последовательность построения

1. Через фронтальную проекцию прямой m₂ провести вспомогательную плоскость-посредник Σ₂, перпендикулярную фронтальной плоскости проекций.

2. При пересечении плоскости Σ₂ с фронтальной проекцией пирамиды получается треугольник с вершинами в точках 1₂2₂3₂.

3. Построить горизонтальную проекцию Δ 1₁2₁3₁.

4. Отметить точки пересечения Δ 1₁2₁3₁ с горизонтальной проекцией прямой m₁ – N_1, К₁; N_2, К₂.

5. Определить видимость прямой m.