Элементы теории графов.
Граф задается парой множеств. Пусть 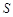 - — непустое множество,
- — непустое множество, 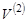 - — множество всех его двухэлементных подмножеств,
- — множество всех его двухэлементных подмножеств, 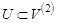 . Тогда пара
. Тогда пара 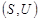 называется неориентированным графом.Элементы множества
называется неориентированным графом.Элементы множества 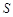 называются вершинами графа, а элементы множества
называются вершинами графа, а элементы множества 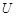 - — ребрами. Итак,
- — ребрами. Итак, 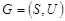 граф - — это конечное множество вершин
граф - — это конечное множество вершин 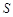 и множество ребер
и множество ребер 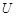 .
.
Вершины графа обозначают по-разному: или большими буквами, или малыми с индексами; для ребер наиболее употребительное обозначение - 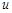 с индексом, например,
с индексом, например, 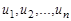 . Взаимное расположение, форма и длина ребер значения не имеют. Важно лишь то, что они соединяют две данные вершины множества
. Взаимное расположение, форма и длина ребер значения не имеют. Важно лишь то, что они соединяют две данные вершины множества 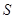 .
.
Если в паре вершин 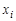 и
и 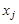 указано направление связи, т. е. какая из вершин является первой, то соединяющий их отрезок
указано направление связи, т. е. какая из вершин является первой, то соединяющий их отрезок 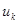 называется дугой, а вершины, определяющие дугу
называется дугой, а вершины, определяющие дугу 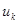 , называют концевыми вершинами. Если концевые вершины совпадают, то дугу называют петлей. В графе
, называют концевыми вершинами. Если концевые вершины совпадают, то дугу называют петлей. В графе 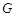 могут существовать дуги (ребра) с одинаковыми концевыми вершинами. Такие дуги называются параллельными.
могут существовать дуги (ребра) с одинаковыми концевыми вершинами. Такие дуги называются параллельными.
Если в графе 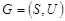 все элементы множества
все элементы множества 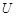 изображаются дугами, то граф называется ориентированным или орграфом, если ребрами, то неориентированным. Два ребра называются смежными, если они имеют общий конец.
изображаются дугами, то граф называется ориентированным или орграфом, если ребрами, то неориентированным. Два ребра называются смежными, если они имеют общий конец.
Вершина 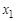 и ребро
и ребро 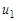 называются инцидентными, если
называются инцидентными, если 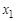 является концом ребра
является концом ребра 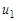 , и не инцидентными в противном случае. Таким образом, смежность есть отношение между однородными элементами графа, тогда как инцидентность является отношением между разнородными элементами.
, и не инцидентными в противном случае. Таким образом, смежность есть отношение между однородными элементами графа, тогда как инцидентность является отношением между разнородными элементами.
Число вершин графа называется его порядком. Степенью 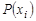 вершины
вершины 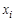 называется число дуг (ребер) графа
называется число дуг (ребер) графа 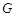 , инцидентных данной вершине. Вершина степени нуль называется изолированной, а если степень равна единице, то такая вершина называется висячей.
, инцидентных данной вершине. Вершина степени нуль называется изолированной, а если степень равна единице, то такая вершина называется висячей.
Граф 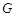 называется простымой, если он не содержит петель и параллельных дуг. Простой граф, в котором каждая пара вершин смежна, называется полным. Граф, содержащий хотя бы две параллельные дуги (ребра), — называется мультиграфом. Граф, содержащий петли, называется — псевдографом.
называется простымой, если он не содержит петель и параллельных дуг. Простой граф, в котором каждая пара вершин смежна, называется полным. Граф, содержащий хотя бы две параллельные дуги (ребра), — называется мультиграфом. Граф, содержащий петли, называется — псевдографом.
Графы удобно изображать в виде рисунков, состоящих из точек и линий, соединяющих некоторые из этих точек. Два графа 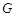 и
и 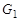 называются изоморфными, если между множеством их вершин существует такое взаимно однозначное соответствие, при котором в одном из графов ребрами соединены вершины в том и только в том случае, если в другом графе ребрами соединены те же вершины. Для орграфов ориентация дуг должна быть также одинаковой.
называются изоморфными, если между множеством их вершин существует такое взаимно однозначное соответствие, при котором в одном из графов ребрами соединены вершины в том и только в том случае, если в другом графе ребрами соединены те же вершины. Для орграфов ориентация дуг должна быть также одинаковой.
Очевидно, что отношение изоморфизма графов является эквивалентностью, т. е. оно симметрично, транзитивно и рефлексивно. Следовательно, множество всех графов разбивается на классы так, что графы из одного класса попарно изоморфны, а графы из разных классов не изоморфны.
Способов задания графов – — великое множество. Самый простой способ – — задание множеств 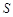 и
и 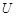 . Граф также может быть задан просто рисунком. В силу изоморфизма один и тот же граф может быть изображен разными рисунками.
. Граф также может быть задан просто рисунком. В силу изоморфизма один и тот же граф может быть изображен разными рисунками.
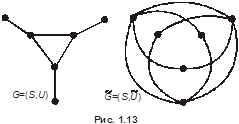
Рис. 1.13.Основной и Определение дополнительныйого графыа
Граф называется плоским (планарным), если он может быть изображен на плоскости так, что все пересечения ребер являются его вершинами. Для произвольного графа 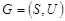 следующим образом определяется дополнительный граф (дополнение)
следующим образом определяется дополнительный граф (дополнение) 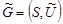 . В этом графе
. В этом графе 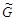 вершин столько же, сколько в графе
вершин столько же, сколько в графе 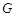 , причем любые две несовпадающие вершины смежны в
, причем любые две несовпадающие вершины смежны в 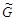 тогда и только тогда, когда они не смежны в
тогда и только тогда, когда они не смежны в 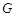 (см. рис. 1.13).
(см. рис. 1.13).
Чередующая последовательность 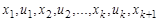 вершин и ребер графа, такая что
вершин и ребер графа, такая что 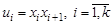 , называется маршрутом, соединяющим вершины
, называется маршрутом, соединяющим вершины 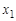 и
и 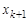 . Очевидно, что маршрут можно задать последовательностью его вершин
. Очевидно, что маршрут можно задать последовательностью его вершин 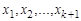 или последовательностью ребер
или последовательностью ребер 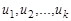 . Маршрут называется цепью, если все его ребра различны, и простой цепью, если все его вершины, кроме, возможно, крайних, различны. Гамильтоновой цепью называется простая цепь, содержащая все вершины графа.
. Маршрут называется цепью, если все его ребра различны, и простой цепью, если все его вершины, кроме, возможно, крайних, различны. Гамильтоновой цепью называется простая цепь, содержащая все вершины графа.
Маршрут называется циклическим, если 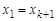 . Циклическая цепь называется циклом, а циклическая простая цепь – — простым циклом. Число ребер в маршруте — называется длинойа маршрута. Гамильтоновым циклом называется простой цикл, содержащий все вершины графа. Длина всякого цикла не менее трех в графе без петель и кратных ребер. Минимальная из длин циклов графа называется его обхватом.
. Циклическая цепь называется циклом, а циклическая простая цепь – — простым циклом. Число ребер в маршруте — называется длинойа маршрута. Гамильтоновым циклом называется простой цикл, содержащий все вершины графа. Длина всякого цикла не менее трех в графе без петель и кратных ребер. Минимальная из длин циклов графа называется его обхватом.
Важным понятием теории графов является связность. Граф называется связным, если любые две его несовпадающие вершины соединены маршрутом.

Рис. 1.14.Граф
В подавляющем большинстве случаев граф задается матрицей. Для расчетов на ЭВМ это единственный способ. Наиболее часто граф задают с помощью матриц смежности и инциденций.
Рассмотрим изображенный на рисунке . 1.14 граф. Как для орграфов, так и для неориентированных графов можно определить матрицу смежности вершин. Это квадратная матрица
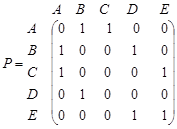
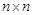 порядка, где
порядка, где 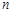 - — число вершин. Ее строки и столбцы соответствуют вершинам графа. Элементы
- — число вершин. Ее строки и столбцы соответствуют вершинам графа. Элементы 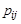 матрицы смежности вершин равны числу дуг, идущих из
матрицы смежности вершин равны числу дуг, идущих из 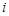 - той вершины в
- той вершины в
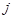 -ю вершину. Если орграф не содержит параллельных дуг, то матрица является бинарной и состоит только из нулей и единиц. В случае неориентированного графа ему вместе с ребром
-ю вершину. Если орграф не содержит параллельных дуг, то матрица является бинарной и состоит только из нулей и единиц. В случае неориентированного графа ему вместе с ребром 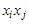 принадлежит и ребро
принадлежит и ребро 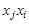 , поэтому матрица смежности вершин будет симметрической. Матрица смежности вершин однозначно определяет структуру графа. Аналогично можно определить и матрицу смежности дуг.
, поэтому матрица смежности вершин будет симметрической. Матрица смежности вершин однозначно определяет структуру графа. Аналогично можно определить и матрицу смежности дуг.
Определим для рассматриваемого графа без ребра 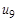 матрицу инциденций. Это прямоугольная матрица размерности
матрицу инциденций. Это прямоугольная матрица размерности 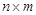 , где
, где 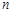 - — число вершин, а
- — число вершин, а 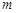 - — число дуг. Элементы
- — число дуг. Элементы 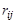 этой матрицы равны плюс единице, если дуга
этой матрицы равны плюс единице, если дуга 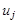 исходит из
исходит из 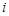 -й вершины (начальная вершина), минус единице, если дуга
-й вершины (начальная вершина), минус единице, если дуга 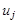 входит в
входит в 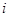 -ю вершину (конечная вершина), нулю, если дуга не инцидентна
-ю вершину (конечная вершина), нулю, если дуга не инцидентна 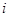 -й вершине. В случае неориентированного графа элементами матрицы будут числа единица и нуль, т. е.
-й вершине. В случае неориентированного графа элементами матрицы будут числа единица и нуль, т. е.
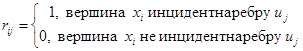 .
.
Строки матрицы инциденций называют векторами инциденций графа  . Матрица инциденций
. Матрица инциденций
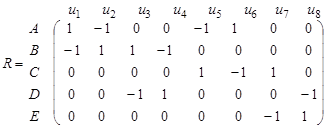
также однозначно определяет структуру графа.
Весьма важным видом графа является связный граф, не имеющий циклов, он называется деревом. В дереве любые две вершины связаны единственным путем.
Рассмотрим связный граф 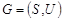 , пусть
, пусть 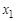 и
и 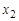 — две его вершины. Длина кратчайшего
— две его вершины. Длина кратчайшего 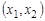 -маршрута называется расстоянием между вершинами
-маршрута называется расстоянием между вершинами 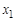 и
и 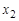 , обозначается через
, обозначается через 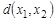 . Очевидно, что расстояние между вершинами является простой цепью и
. Очевидно, что расстояние между вершинами является простой цепью и 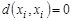 . Для любой вершины
. Для любой вершины 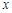 величина
величина
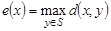 (1.13.6)
(1.13.6)
называется эксцентриситетом вершины 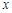 . Максимальный из всех эксцентриситетов вершин называется диаметром графа и обозначается
. Максимальный из всех эксцентриситетов вершин называется диаметром графа и обозначается 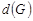 , т. е.
, т. е.
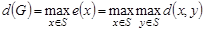 . (1.13.7)
. (1.13.7)
Минимальный из эксцентриситетов вершин графа называется его радиусом и обозначается через 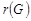 :
:
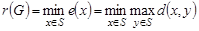 . (1.13.8)
. (1.13.8)
Вершина 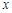 периферийная, если ее эксцентриситет равен диаметру графа, т. е.
периферийная, если ее эксцентриситет равен диаметру графа, т. е. 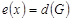 . Простая цепь, расстояние между концами которой равно
. Простая цепь, расстояние между концами которой равно 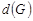 , называется диаметральной цепью.
, называется диаметральной цепью.
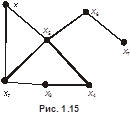
Рис. 1.15.Центр графа
 |
Вершина
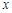 центральная, если
центральная, если  . Множество всех центральных вершин графа называется его центром. Центром может быть единственная вершина графа или несколько вершин. На рис. 1.15
. Множество всех центральных вершин графа называется его центром. Центром может быть единственная вершина графа или несколько вершин. На рис. 1.15 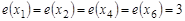 ,
, 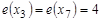 ,
, 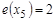 . Таким образом,
. Таким образом, 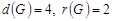 . Периферийные вершины
. Периферийные вершины 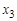 и
и 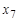 , диаметральные цепи
, диаметральные цепи 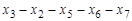 и
и 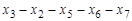 , центральная вершина
, центральная вершина 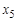 .
.
[1] Клод Элвуд Шеннон (1916—2001 гг.) — американский математик.
* Клод Элвуд Шеннон (1916 – 2001) – американский математик.
[2] Ральф Хартли (1881—1970 гг.) — американский инженер и изобретатель.
* Ральф Хартли (1881 – 1970) – американский инженер и изобретатель.
[3] Джино Фано (1871—1952 гг.) — итальянский математик.
* Джино Фано (1871 – 1952) – итальянский математик.
[4] Огастес Морган (де Морган) (1806—1875 гг.) — шотландский математик и логик.
* Огастес Морган (де Морган)(1806 – 1875) – шотландский математик и логик.
[5] Леонард Эйлер (1707—1783 гг.) — швейцарский математик.
* Леонард Эйлер (1707 - — 1783) - — швейцарский математик.
[6] Джон Венн (1834—1923 гг.) — английский математик и логик.
** Джон Венн (1834 - — 1923) - — английский математик и логик.
[K1]От "пиксел"
[K2]Почему в разные стороны / или \?
[S3]Как мне разъяснили наши ‘русистки’ слово пиксель склоняется след. образом:
пиксель пиксели
пикселя пикселей
пикселю пикселям
пиксель пиксели
пикселем пикселями
пикселе пикселях
Знак / в теории множеств используется для записи после него дополнительных условий, а знак \ для обозначения разности множеств.
Дата добавления: 2016-06-05; просмотров: 4187;










