Характеристические числа и характеристические векторы

От характеристических векторов зависят динамические свойства системы. Рассмотрим векторное уравнение

y = Ax,

где у – вектор входа (n×1); x – вектор выхода (n×1); А – квадратная матрица (n×n).

Вопрос о нахождении характеристических значений связан с вопросом: существует ли такой вектор x, который в результате его преобразования с помощью матрицы А переходит в вектор y, имеющий то же направление в пространстве что и вектор x. Если такой вектор x существует, то это значит, что yпропорционален x(рис. 2.11):

y = Ax = λx,

где λ – скаляр.

Рис. 2.11. Характеристический вектор y= λx

Перенесем λx = λExв левую часть:

(λE – A)x= 0,

где E – единичная матрица.

Это векторно-матричное уравнение можно записать в виде равносильной системы скалярных уравнений, соответствующих строкам матрицы А:

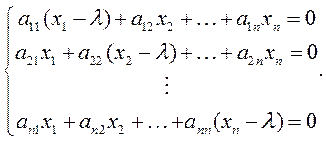
Данная система имеет нетривиальное решение в том случае, если определитель матрицы коэффициентов равен нулю:

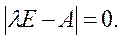
Раскрытие данного определителя приводит к характеристическому уравнению:

.

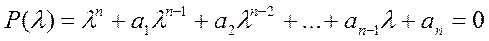Многочлен n-й степени относительно l называется характеристическим многочленомматрицы А.Корни этого уравнения равны характеристическим (собственным) значениям матрицы А. Особый интерес представляют коэффициенты многочлена а₁ и а_n.

Если положить λ = 0, то:

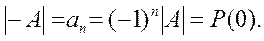
Представим

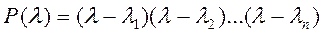
и снова положим, что λ = 0. Тогда

,

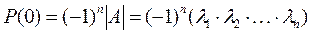откуда

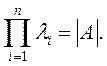
Таким образом, произведение характеристических чисел равно определителю матрицы А. В случае равенства нулю какого-нибудь из характеристических чисел матрица А становится особенной (вырожденной).

Раскрывая характеристическое уравнение, записанное в виде произведения сомножителей, можно выразить коэффициенты при различных степенях λ через характеристические числа.

Выразим коэффициент при λ^n-1:

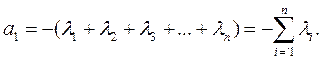
С другой стороны, раскрывая также определитель |λE–A|, найдем, что коэффициент при λ^n-1 равен со знаком минус сумме диагональных элементов матрицы А:

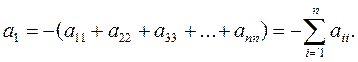
Таким образом, сумма диагональных элементов квадратной матрицы равна сумме ее характеристических чисел:

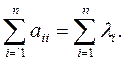
Ввиду важности этого свойства сумме диагональных элементов матрицы присвоено особое название: след матрицы. Обозначим след матрицы:

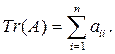
Формула Бохера

Можно записать полезную рекуррентную формулу, выражающую коэффициенты характеристического уравнения через следы матриц различного порядка T_k = Tr(A^k):

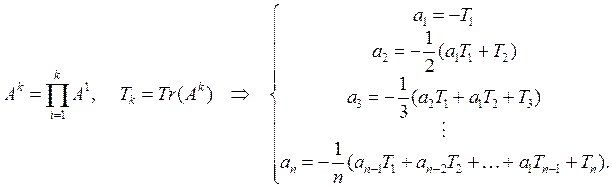
Эта формула, известная как формула Бохера, эффективна при вычислении коэффициентов характеристического уравнения с помощью компьютерной программы.

Пример. Найти характеристические числа следующей заданной матрицы А:

.

По формуле Бохера: a₁ = – T₁= – (2+1–1)= – 2. Произведение матрицы А на себя:

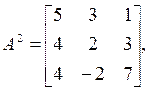
откуда

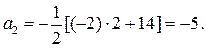
Аналогично

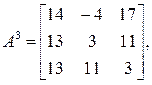
откуда

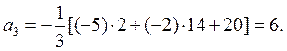
Следовательно, характеристическое уравнение имеет вид:

λ+2λ–5λ=(λ–1)(λ+2)(λ–3)=0.

Найдем характеристические числа: λ₁ = 1, λ₂ = – 2, λ₃ = 3.

Модальная матрица

Для каждого из n характеристических чисел λ_i (i=1,2,…,n) матрицы А (в предположении, что все они различны) можно получить решение уравнения [λE –A]x = 0. Это векторно-матричное уравнение можно представить в виде системы уравнений

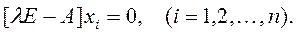
Векторы x_i, представляющие собой решения данной системы уравнений, являются характеристическими векторами матрицы A. Поскольку эта система уравнений однородная, то и k_ix_i, где k_i – произвольная скалярная величина, также служит решением. Поэтому эта система уравнений определяет однозначно только направление каждого из x_i.

Матрица, образованная векторами-столбцами k_ix_i, называется модальной матрицей. (Модальная – от слова “mode”, означающего «частота». Так называемые «частоты», описывающие динамику линейной системы, могут быть выражены в виде составляющих движения вдоль характеристических векторов).

При различных характеристических числах столбцы модальной матрицы могут выбираться равными или пропорциональными произвольному столбцу присоединенной матрицы Adj[λE – A].

Это вытекает из того факта, что [λE – A] имеет ранг n – 1. Поскольку определитель |λE – A|=0 (как мы уже выяснили), ранг матрицы Adj[λE– A] должен быть меньше n, однако при этом он не может быть меньше n – 1, так как тогда равнялись бы нулю все (n – 1) миноров строки определителя |λE– A|, что, в свою очередь, потребовало бы, чтобы

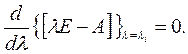
Отсюда следует, что λ_i является кратным корнем исходной системы уравнений, а это противоречит предположению о том, что характеристические числа различны. Таким образом, матрица [λE – A] имеет ранг (n – 1), поэтому из определения присоединенной матрицы следует, что столбцы модальной матрицы пропорциональны произвольному ненулевому столбцу Adj [λE – A]. Ввиду линейной зависимости столбцов Adj [λE – A] для данного λ_i выбор каждого λ_i определяет только один столбец модальной матрицы.

Пример. Найти характеристические числа и модальную матрицу, соответствующую матрице А:

.

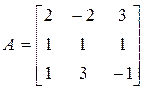Характеристическое уравнение находим из условия |λE –A|=0:

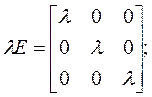
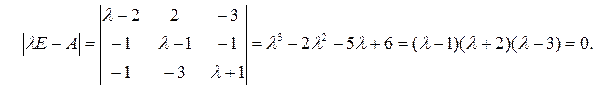
Характеристические числа: λ₁ = 1, λ₂ = –2, λ₃ = 3.

Присоединенная матрицаравна:

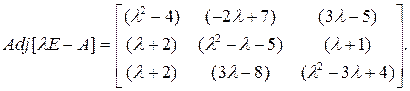
Чтобы найти модальную матрицу, необходимо в присоединенную матрицу подставить значение собственных (характеристических) чисел.

При λ₁ = 1присоединенная матрица равна

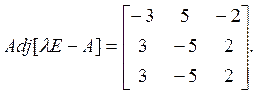
При λ₂ = –2присоединенная матрица равна

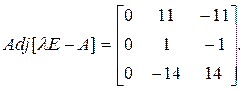
При λ₃ = 3присоединенная матрица равна

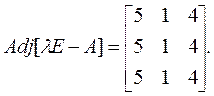
Поскольку характеристические векторы единственным образом определяют только направление, то умноженные на скалярную величину, они также будут удовлетворять уравнению

.

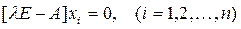Следовательно, модальная матрица имеет вид:

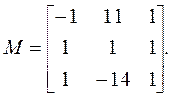
Каждый столбец данной модальной матрицы служит характеристическим вектором в одномерном векторном пространстве. Три столбца модальной матрицы образуют базисв соответствующем трехмерном векторном пространстве.

Выше рассматривалась модальная матрица при различных характеристических числах А. В случае кратных характеристических чисел и несимметрической А определение независимых модальных столбцов не очевидно, так как не существует однозначного соответствия между порядком кратности корня характеристического уравнения и дефектом соответствующей характеристической матрицы [λE–A]. Однако и в этом случае вопрос построения модальной матрицы решается положительно, хотя и более сложно.