Исследование функции с помощью производной

1. Необходимое условие возрастания и убывания функции.

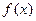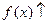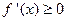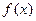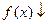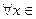
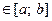Т1. Если дифференцируемая функция возрастает ( ) на сегменте , то ее первая производная . Если дифференцируемая функция ( ) убывает на сегменте , то ее первая производная .

2. Достаточное условие возрастания и убывания функции.

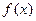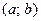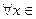
Т2. Пусть функция непрерывна на сегменте и дифференцируема на интервале . Если ее первая производная 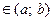, то функция возрастает на сегменте . Если ее первая производная 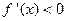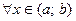, то функция убывает на сегменте .

3. Условия постоянства функции на сегменте .

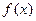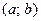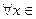
Т3. Пусть функция непрерывна на сегменте и дифференцируема на интервале . Если ее первая производная 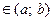, то функция постоянна на сегменте .

Пример 1. Исследовать функцию =x³-3x-4 на монотонность.

Решение: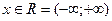

+ - +

Х

-1 1

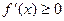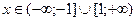
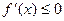при

при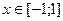

Ответ: даннаяфункция возрастает при 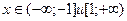и убывает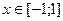

4. Минимум и максимум (экстремумы) функции.

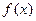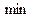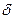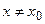О1. Функция имеет в точке минимум ( ), если существует та-кая -окрестность точки , что значение функции в любой другой точке из 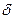-окрестность точки превышает значение функции в самой точке , т.е. выполняется неравенство .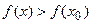

Обозначение .

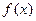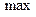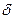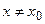О2. Функция имеет в точке максимум ( ), если существует такая -окрестность точки , что значение функции в любой другой точке из 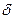-окрестность точки меньше значения функции в самой точке , т.е. выполняется неравенство .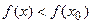

Обозначение .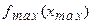

Пример 2. Найти на заданном графике точки максимума и минимума (Рис. 80).

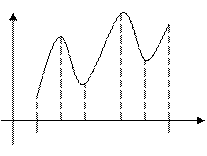
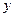
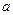
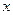Рис. 80. Максимумы и минимумы задан-

ной функции.

О3. Точки минимума и максимума объединяются под общим названием точки экстремума.

5. Необходимое условие существования экстремума функции.

Т4. Если дифференцируемая функция 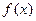имеет в точке экстремум, то ее первая производная в этой точке равна нулю, т.е. .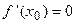

PS.5. Обращение в нуль первой производной функции в точке является необходимым, но не достаточным условием существования экстремума в этой точке. Непрерывная функция может иметь экстремум в точке даже в том случае, когда ее первая производная в этой точке не существует. В этом случае говорят об “острых” экстремумах.

Пример3. Доказать, что функция имеет “острый” экстремум в точке .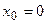

О4. Точки, в которых первая производная функции обращается в нуль или не существует, называются критическими (стационарными или подозрительными на экстремум).

PS.6. Всякая точка экстремума является критической точкой, однако не любая критическая точка будет экстремумом.