Основные аксиомы статики

ОСНОВНЫЕ ПОЛОЖЕНИЯ И АКСИОМЫ СТАТИКИ. Основные понятия статики

Статика есть часть теоретической механики, изучающая условия, при которых тело находится в равновесии. Равновесием будем считать такое состояние, когда тело находится в покое или движется прямоли­нейно и равномерно.

Тело называют абсолютно твердым (или абсолютно жестким), если расстояние между любыми его точками не меняется при дей­ствии на него других тел. Абсолютно твердых тел в природе нет, но во многих случаях изменения формы и размеров (деформации) тел настоль­ко незначительны, что ими можно пренебречь. В теоретической механике полагают тела абсолютно твердыми и физико-механические свойства их не учитывают (за исключением вопросов, связанных с трением).

Материальной точкой называется точка, имеющая массу. Материальной точкой мы будем считать не только тело, имеющее очень малые размеры, но и любое тело, размерами которого в условиях данной задачи можно пренебречь. Например, в астрономии звезды рассматрива­ют как материальные точки, так как размеры звезд малы по сравнению с расстояниями между ними. Одно и то же реальное тело в зависимости от постановки задачи может рассматриваться либо как материальная точка, либо как тело, размеры которого необходимо учесть. Всякое тело можно полагать взаимосвязанной совокупностью (системой) материальных то­чек. Абсолютно твердое тело представляет собой неизменяемую систему материальных точек.

Тело называется свободным, если никакие другие тела не пре­пятствуют его перемещению в любом направлении, в противном случае тело называется несвободным или связанным. Пример свобод­ного тела — воздушный шар в полете. Большинство окружающих нас тел являются несвободными телами.

Тела в природе различным образом взаимодействуют между собой или с окружающей их средой. Механическое взаимодействие тел, т. е.

взаимодействие, влияющее на их состояние покоя или движения (механи­ческое состояние), характеризуется силой.

Сила есть мера механического взаимодействия тел.Сила характери­зуется тремя элементами: числовым значением, направлением и точкой при­ложения. Таким образом, сила — величина векторная. Числовое значение силы называется модулем вектора силы. Направление силы есть направление того движения, которое получила бы покоящаяся сво­бодная материальная точка под действием этой силы. Прямая линия, по кото­рой направлен вектор силы, называется л и н и е й действия силы.

Как известно из физики, Международная система единиц (СИ) в ка­честве единицы силы устанавливает ньютон (Н).

Ньютон есть сила, сообщающая телу массой 1 кг ускорение 1 м/с² в направлении действия силы.

Кратные и дольные единицы силы образуются путем умножения или деления основной единицы на степень числа 10. Согласно ГОСТу, их на­звания образуются прибавлением десятичных приставок:

мега (М).................. 10⁶ деци (д).................. 10 ^-1

кило (к)................... 10 ³ санти (с)................ 10 ^-2

гекто (г)................... 10 ² милли (м).............. 10 ^-3

дека (да).................. 10 микро (мк)............. 10^-6

Например, килоньютон (кН) = 10³ Н, меганьютон (МН) = 10⁶ Н, миллиньютон (мН)=10^-3Н.

Графически силу изображают отрезком прямой со стрелкой; длина отрезка в определенном масштабе равна модулю вектора силы (рис. 1.1). Масштаб силы показывает, сколько единиц модуля силы со­держится в единице длины ее век­тора. Единица масштаба силы, например, = Н/мм или Н/см.

На рис. 1.1 изображена сила, приложенная в точке А и дейст­вующая по линии тп.Вектор си­лы обозначим прописной латин­ской жирной буквой F, а модуль силы — той же буквой, но светлой F*.Для вектора силы F точка А

* В некоторых книгах векторы обозначают светлыми латинскими буквами со стрелочкой (или черточкой) над ними, а модули — той же буквой без стрелочки. Этот способ следует применять при написании векторных равенств на классной доске.

будет называться началом, а точка В — концом вектора. Нередко удобно изображать вектор силы так, чтобы стрелка, стоящая в конце вектора, упиралась в точку приложения силы (сила Q на рис. 1.1).

Совокупность тел (в том числе материальных точек), каким-то обра­зом связанных между собой, назовем системой тел. Силы взаимо­действия между телами, входящими в данную систему, называют внут­ренними, а силы, с которыми действуют на данную систему другие тела, — внешними. Если данную систему рассечь на части и рассмат­ривать равновесие каждой части в отдельности, то внутренние для всей системы силы, действующие в сечениях, станут внешними силами для соответствующих частей системы. Такой метод позволяет определить внутренние силы, действующие в сечениях, и называется методом сече­ний. В технической механике он применяется весьма широко. Следует заметить, что деление сил на внешние и внутренние условно и зависит от постановки задачи и даже метода ее решения.

Основные аксиомы статики

Условия, при которых тело может находиться в равновесии, выво­дятся из нескольких основных положений, принимаемых без доказа­тельств, но подтвержденных опытом и называемых аксиомами статики. Основные аксиомы статики сформулированы английским ученым Ньютоном (1642—1727) и поэтому названы его именем.

Аксиома I (аксиома инерции, или первый закон Ньютона).

Всякое тело сохраняет свое состояние покоя или прямолинейного равномерного движения, пока какие-нибудь силы не выведут тело из этого состояния.

Способность материального тела сохранять движение при отсут­ствии действующих сил или в постепенном изменении этого движе­ния, когда на тело начинают действовать силы, называется инер­цией или инертностью. Инертность есть одно из основных свойств материи.

На основании этой аксиомы состоянием равновесия счи­таем такое состояние, когда тело находится в покое или движется прямо­линейно и равномерно, т. е. по инерции.

Аксиома П(аксиома взаимодействия, или третий закон Ньютона).

Силы взаимодействия между собой двух тел всегда равны по моду­лю и направлены по одной прямой в противоположные стороны.

Из третьего закона Ньютона вытекает, что одностороннего механи­ческого действия одного тела на другое не существует, т. е. все силы при­роды — силы парные.

Совокупность сил, приложенных к данному телу (или системе тел), называется системой сил. Сила действия какого-либо тела на данное и сила противодействия не представляют собой систему сил, так как они приложены к различным телам.

Если какая-нибудь система сил обладает таким свойством, что после приложения к свободному телу она не изменяет его механическое состоя­ние, то такая система сил называется уравновешенной.

Аксиома III(у с л о в и е равновесия двух сил).

Для равновесия свободного твердого тела, находящегося под дейст­вием двух сил, необходимо и достаточно, чтобы эти силы были равны по модулю и действовали по одной прямой в противоположные стороны.

Условие, сформулированное в этой аксиоме, является необходимым для равновесия двух сил. Это значит, что если система двух сил находит­ся в равновесии, то эти силы должны быть равны по модулю и действо­вать по одной прямой в противоположные стороны.

Условие, сформулированное в этой аксиоме, является достаточным для равновесия двух сил. Это значит, что справедлива обратная формули­ровка аксиомы, а именно: если две силы равны по модулю идействуют по одной прямой в противоположные стороны, то такая система сил обя­зательно находится в равновесии.

В дальнейшем мы познакомимся с условием равновесия, которое бу­дет необходимо, но не достаточно для равновесия.

Аксиома IV.

Равновесие (как и любое другое механическое состояние) твердого тела не нарушится, если к нему приложить или удалить систему урав­новешенных сил.

Следствие из аксиом III и IV.

Механическое состояние твердого тела не нарушится от перенесе­ния силы вдоль линии ее действия.

Докажем это следствие. Пусть на твердое тело действу­ет в числе других сила Р, при­ложенная в точке А,с линией действия аb (рис. 1.2). В произ­вольно взятой на линии аb точ­ке В приложим две равные по модулю и противоположно на­правленные силы Р₁ и Р₂, дей­ствующие по линии аb.Соглас-

но аксиоме III, силы P₁ и Р₂ взаимно уравновешены, а на основании ак­сиомы IV их можно приложить к телу, не нарушая механического состоя­ния. Подберем силы P₁ и Р₂ такими, чтобы они по модулю были равны силе Р:

На основании аксиомы IV отбросим силы Р₁ и Р₂, как взаимно урав­новешенные. Тогда оставшуюся силу Р₁ можно рассматривать как силу Р, перенесенную из точки А в точку В по линии действия, причем механиче­ское состояние не нарушается. Следствие доказано.

Подчеркнем, что перенос силы вдоль линии ее действия можно осу­ществлять лишь в том случае, если рассматриваемое тело абсолютно твердое.

Две различные системы сил принято считать эквивалентными, если одну из них можно заменить другой, не нарушая механического со­стояния свободного твердого тела.

Следует заметить, что эквивалентные системы сил могут вызывать различные деформации нетвердого тела.

На рис. 1.3 изображены две системы сил, порознь действующие на один и тот же стержень АВ,причем P₁ = P₂ ,a Q₁= Q₂ .На основании ак­сиомы III ясно, что каждая из этих систем не выводит стержень из равно­весия, т. е. они эквивалентны. Но система сил (Р₁, P₂) стремится укоро­тить стержень, а система сил (Q₁, Q₂) удлинить его. Эквивалентность сис­тем сил условимся записывать так:

На основании следствия из аксиом III и IV можно сказать, что две силы эквивалентны,если они равны по модулю и действуют по одной прямой в одну сторону. Два вектора силы (как и два любых однородных по размерности вектора) равны, если они параллельны, одинаково на­правлены и имеют равные модули.

Одна сила, эквивалентная данной системе сил, называется равно­действующей, а силы этой системы — составляющими этой равнодействующей.

Сила, которая уравновешивает данную систему сил, называется

уравновешивающей этой системы.

Равнодействующая и уравно­вешивающая силы одной и той же системы равны по модулю и дей­ствуют по одной прямой в проти­воположные стороны. Равнодей-

ствующая уравновешенной системы сил равна нулю, иначе говоря, урав­новешенная система сил эквивалентна нулю.

АксиомаV(аксиома параллелограмма).

Равнодействующая двух сил, приложенных к телу в одной точке, равна по модулю и совпадает по направлению с диагональю параллело­грамма, построенного на данных силах, и приложена в той же точке.

Построение диагонали параллелограмма (рис. 1.4, а),сторонами ко­торого являются заданные векторы, называется векторным или геометрическим сложением. Таким образом, можно сказать, что равнодействующая двух сил, приложенных в одной точке, равна их век­торной сумме

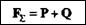
и приложена в той же точке.

Равнодействующую двух сил можно найти, построив вместо паралле­лограмма сил треугольник сил (рис. 1.4, б). Из рис. 1.4, б видно, что поря­док сложения векторов на величину равнодействующей не влияет, т. е.

Модуль и направление равнодействующей двух сил, приложенных в одной точке, можно определить аналитически, для чего рассмотрим треугольник ABC (рис. 1.4, а).

По теореме косинусов

откуда модуль равнодействующей

По теореме синусов

откуда найдем направление равнодействующей:

Рассмотрим частные случаи сложения двух сил:

Равнодействующая двух сил, действующих по одной прямой в одну сторону, равна их сумме и направлена по той же прямой в ту же сторону;

Равнодействующая двух сил, действующих по одной прямой в раз­ные стороны, равна разности этих сил и направлена по той же прямой в сторону большей силы;

Равнодействующая двух сил, действующих под прямым углом, равна по величине диагонали прямоугольника, построенного на данных силах.