Что такое ТЕПЛОЁМКОСТЬ
При поступлении теплоты температура системы повышается. В случае бесконечно малого изменения температуры справедлива пропорциональность
dT=δQ , или dT=constδQ
Это соотношение удобнее написать в виде: δQ=СdT или
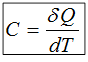
Величина С называется истинной теплоемкостью системы.
Теплоемкость — это отношение количество теплоты, подведенная к системе, к тому изменению температуры, которая при этом происходит.
Кроме истинной, различают ещё и среднюю теплоемкость: 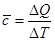
Теплоемкость
| Истинная, [Дж/К] | Мольная , [Дж/моль*К] 1 моль вещества | Удельная, [Дж/кг*К] 1 кг вещества |
| Экстенсивная величина | Интенсивные величины | |
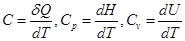
| 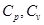
|
Если теплоёмкость отнести к единице массы (молю) вещества, то она становиться независимой от массы всей системы и приобретает свойства интенсивного параметра. Если теплоёмкость относиться к единице массы вещества, она называется удельной, а к 1 моль- мольной теплоёмкостью с размерностью Дж/(моль*к)
Мы будем рассматривать только мольные теплоёмкости, т.к. для них все закономерности значительно проще, чем для удельной теплоёмкости.
Теплоёмкость зависит от условий, в которых осуществляется переход теплоты к системе. Если система заключена в постоянный объём, то повышение температуры на dT произойдёт под действием теплоты, равный CvdT , где Cv - теплоёмкость при постоянном объёме. В случаи постоянства давления при расширении системы для повышения температуры на dT потребуется теплоты CpdT, где Cp - теплоёмкость при постоянном давлении.
С учётом условий перехода теплоты, когда одна или несколько переменных поддерживаются постоянными, а другие изменятся, теплоёмкость можно выразить при помощи частных производных: 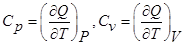 . Так как δQv= dU,
. Так как δQv= dU,
δQp =dH, можно записать:
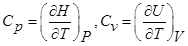 (1)
(1)
Cv– изохорное теплоёмкость газов, Cp– изобарное теплоёмкость газов.
Различия между изохорной и изобарной теплоёмкостями обусловлены различием внутренней энергии и энтальпии. Изменения энтальпии и внутренней энергии отличаются на величину работы, совершаемой системой.
δW=∆nRT, ∆H—∆U=∆nRT
Поэтому теплоёмкости при постоянном объёме Cv и постоянном давлении Cp также отличаются на величину работы: Cp - Cv = δW
На основании выражений (1) можно записать:
dU= CvdT
dH= CpdT
Подставив эти равенства в уравнение ∆H- ∆U=∆nRT
и учитывая, что ∆n= 1, найдём связь мольных теплоёмкостей газов:
Cp– Cv= Rили Cp= Cv+ R
Как видно, они различаются на величину газовой постоянной.
Из условия Cp= Cv+ Rследует, что Cp˃Cv, т.е в изобарном процессе, когда P=const, для повышения температуры системы требуется большее количество теплоты, чем в изохорном процессе.
Мольная теплоёмкость газов имеет значения порядка R, поэтому различие между Cpи Cvвесьма существенно. Так, для диоксида углерода СО2 при 250С Ср = 37, 14;а Сv=28,83 Дж/(моль*К)
Разность Ср – Сvпредставляет собой работу изобарного расширения одного моля идеального газа при повышении температура на один градус. Жидкости и твёрдости тела характеризуются незначительным увеличением объёма при нагревании. Поэтому для конденсированных тел можно считать, что Ср ≈ Сv.
УРАВНЕНИЕ КИРХГОФА. ЗАВИСИМОСТЬ ТЕПЛОВЫХ ЭФФЕКТОВ ОТ ТЕМПЕРАТУРЫ.
Рассмотренные ранее расчеты тепловых эффектов на основе закона Гесса по теплоте образования и сгорания ограничены стандартными условиями. Для практических целей необходимо рассчитать тепловые эффекты для конкретных условий, отличных от стандартных.
Перейти от известных тепловых эффектов при стандартных условиях, т.е. при температуре 250С(298,15К) и давлении 1 атм. (1,013*105Па), к расчету тепловых эффектов при любой интересующей нас температуре можно, используя закон Кирхгофа. Процессы в промышленных условиях характеризуются значительным варьированием температуры, диапазон которой определяется не только условиями технологи, но и сезоном.Этот диапазон может достигать сотни градусов - естественно, что тепловые эффекты будут существенно различными и зависеть от температуры.
Рассмотрим закон Кирхгофа в дифференциальной форме. Для этого запишем изменения энтальпии в изобарном и внутренней энергии в изохорном процессах.
∆H = H2—H1; ∆U = U2—U1.
Продифференцируем эти уравнения по температуре и получим:
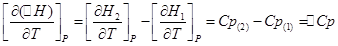
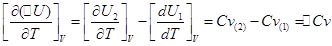
Уравнения Кирхгофа:
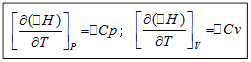
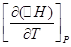 и
и 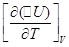 — температурные коэффициенты теплового эффекта изобарного и изохорного процессов соответственно;
— температурные коэффициенты теплового эффекта изобарного и изохорного процессов соответственно; 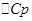 и
и  — изменение теплоемкости системы в результате изобарного и изохорного процессов соответственно.
— изменение теплоемкости системы в результате изобарного и изохорного процессов соответственно.
На основание уравнения Кирхгофа формулируется закон Кирхгофа в дифференциальной форме: температурный коэффициент теплового эффекта процесса равен изменению теплоемкости системы, происходящему в результате этого процесса.
Таким образом, закон Кирхгофа в дифференциальной форме позволяет определить лишь изменение теплового эффекта с изменением температуры, а не величину самого теплового эффекта.
Проанализируем уравнение Кирхгоф
Для реакции: aA + bB = dD+ rR при изобарном процессе (р=const) по закону Кирхгофа изменение теплоемкости в системе будет иметь вид:
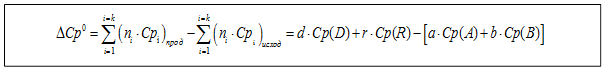
Аналогичное выражение можно получить для изохорного процесса:
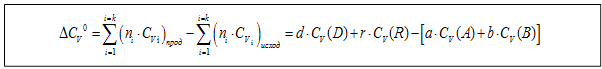
Так как закон Кирхгофа позволяет определить изменения теплового эффекта процесса с изменением температуры, строим график:
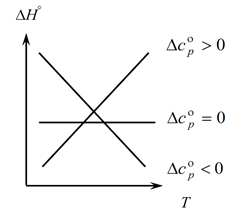
1. Рассмотрим первый случай, когда ∆Ср(∆Сv)˃0, т.к. ∆Ср=∑Скон.—∑Снач., отсюда вытекает, что сумма теплоемкостей продуктов реакций больше суммы теплоемкостей исходных веществ: ∑Скон.˃∑Снач. В этом случае получаем кривую 1 на графике, которая означает, что при увеличении температуры изменение теплового эффекта процесса также увеличивается (Т↑ и ∆H↑);
2. Второй случай, когда ∆Ср(∆Сv)˂0. Аналогично первому закону имеем ∑Скон.˂∑Снач. (сумма теплоемкостей конечных продуктов меньше суммы теплоемкостей начальных веществ). Тогда на графике получаем кривую, которая означает, что при увеличении температуры изменение теплового эффекта процесса уменьшается (Т↑→∆H↓)
3. И третий случай, когда изменение теплоемкостей системы равна нулю ∆Ср(∆Сv)=0. Тогда сумма теплоемкостей конечных продуктов реакций равна сумме теплоемкостей исходных веществ ∑Скон.=∑Снач. В этом случае тепловой эффект реакции не является функцией от температуры (∆H ≠ f(T)) и на графике получаем прямую.
РАСЧЕТ ТЕПЛОВЫХ ЭФФЕКТОВ ПРИ ЗАДАННОЙ
ТЕМПЕРАТУРЕ. ИНТЕГРИРОВАНИИ УРАВНЕНИЯ КИРХГОФА
Чтобы найти значение теплового эффекта в зависимости от температуры, неоюходимо проинтегрировать уравнения
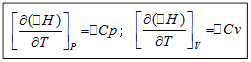
От Т до Т0 (где Т — требуемая температура, Т0 — стандартная температура), от ∆H до ∆H0 или от ∆U до ∆U0 (где ∆H и ∆U — энтальпия и внутренняя энергия в условиях, отличающихся от стандартных). Интегрирование проводится для двух случаев:
| Интегрирование | |
| Приближенное, т.е. изменение теплоемкости не зависит от температуры | Точное, т.е. изменение теплоемкости зависит от температуры |
| ∆Ср≠f(T) ∆Cv≠f(T) ∆Ср=const, ∆Cv=const | ∆Ср=f(T) ∆Cv=f(T) ∆Ср≠ const, ∆Cv≠ const |
Для неорганических веществ: Для органических веществ:
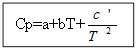
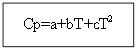
Пример: для H2(г)- неорганическое вещество
| Ср=f(T) | Т | |||
| a | b*103 | c’*10-5 | 289-3000 | |
| 27,28 | 3,26 | 0,50 | ||
Ср(Н2(г))=27,28+3,26*10-3Т+ 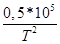 .
.
а) Приближенное интегрирование:
для изобарного процесса
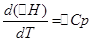



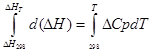
∆HT - ∆H298=∆Cp*(T-298)
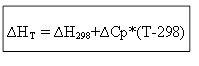
для изохорного процесса:
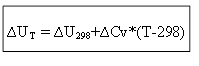
Таким образом, для определения теплового эффекта ∆H или внутренней энергии ∆U при любой температуре Т необходимо знать теплоту процесса в стандартных условиях ∆H0 (∆U0) и изменение теплоемкостей ∆Ср, ∆Cv.
Пример. Рассчитаем тепловой эффект ∆H процесса получения бензола из ацетилена:
3С2Н2(г)→С6Н6(г) при 750С(348К).
Решение:
1.Находим по таблицам среднее мольное изобарные теплоемкости бензола и ацетилена:
СрС6Н6(г) = 81,67Дж/(моль*К);
СрС2Н2(г) = 43,93Дж/(моль*К).
2.Находим изменение теплоемкости процесса:
∆Ср=∑(nСр)кон — ∑(nСр)нач = СрС6Н6(г) — 3* СрС2Н2(г)= 81,67 — 3*43,93 = - 50,12 Дж/(моль*К).
3. По табличным данным находим тепловой эффект в стандартных условиях:
∆H0 = ∆H0обр С6Н6(г) — ∆H0обр С2Н2(г) = 82,93 – 3*226,73 = - 597,26 кДж/моль
4. Находим тепловой эффект при заданной температуре:
∆H = ∆H0+∆Ср(Т-Т0)= - 597,26*103 +(-50,12)*(348- 298) = -599766 Дж/моль
б) Точное интегрирование:
Рассмотрим второй, более сложный случай, когда изменение теплоемкости зависит от температуры, т.е. Ср=f(T), Cv=f(T).
Обратимся к уравнению реакции в общем виде
dD + rR = qQ+ pP
| a | b*103 | c’*10-5 | C*106 | |
| D | + | + | - | + |
| R | + | + | + | - |
| Q | + | + | + | - |
| P | + | + | + | - |
∆a=q*a(Q) + p*a(P) — [d*a(D) + r*a(R)];
∆b=q*b(Q) + p*b(P) — [d*b(D) + r*b(R)];
∆c’= q*c’(Q) + p*c’(P) — [r*c’(R)];
∆c= -dc(D)
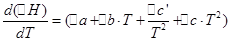
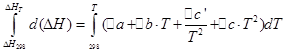
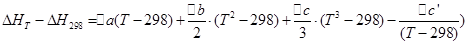
Те же операции проведем для изохорного процесса:
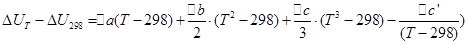
При помощи этих уравнений можно рассчитать тепловой эффект реакции при любой температуре, зная тепловой эффект реакции в стандартных условиях, который определяют по теплотам образования или сгорания.
ТЕПЛОТА РАСТВОРЕНИЯ
Изменение энтальпии при переходе твердого, жидкого или газообразного вещества в раствор называют тепловой или энтальпией растворения.
Теплота растворения в общем случае включает в себя теплоты разрушения кристаллической решетки (для твердых веществ), ионизация и сольватация.
Для разрыва связи между ионами кристаллической соли необходима энергия, т.е. при этом теплота поглощается. В то же время в водном растворе происходит гидратация ионов, т.е. образуется связь между ионами и молекулами Н2О. Знак теплоты растворения определяется тем процессом, который энергетически сильнее выражен.
LiBr: ∆Hраст = - 49,02 кДж/моль – теплота выделяется
КСl: ∆Hраст = 7,23 кДж/моль – теплота поглощается
Различают: интегральную теплоту растворения — это та теплота, которая выделяется или поглощается при растворении 1 моля данного вещества с образованием раствора данной концентрации. Интегральная теплота растворения изменяется в зависимости от количества растворяемого вещества.
Различают: дифференциальную теплоту растворения — эта та теплота, которая сопровождает растворение 1 моля данного вещества в бесконечно большом объеме раствора данного вещества. Интегральные теплоты широко используются в расчетах теплот образования и теплот других реакций по закону Гесса. Дифференциальные теплоты растворения характеризуют термодинамические свойства растворов и процесс их образования.
| <== предыдущая лекция | | | следующая лекция ==> |
| Промышленные способы подвода и отвода теплоты в химическом производстве. | | | Теоретические основы ПАХТ. |
Дата добавления: 2017-09-01; просмотров: 3532;










