Учет симметрии при определении перемещений.

При симметричной расчетной схеме балки и симметричной нагрузке эпюра прогибов симметричная, а эпюра углов поворота сечений кососимметричная. Рассмотрим шарнирно опертую балку, загруженную в середине пролета сосредоточенной силой 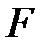(рис.14.1 ) Легко видеть, что максимальный прогиб 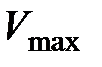возникает в середине пролета балки, следовательно, угол поворота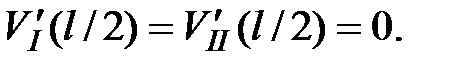

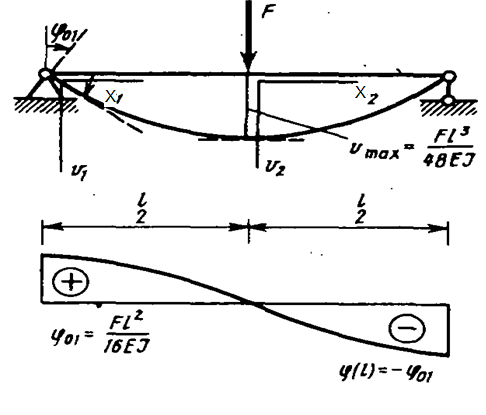
Рис. 14.1 Учет симметрии при определении перемещений

Таким образом, достаточно записать уравнения для функции прогибов и функции углов поворота сечений только на первом участке:

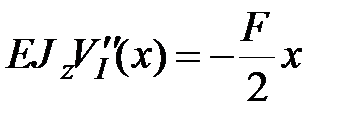
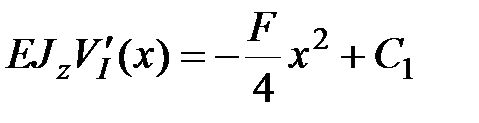
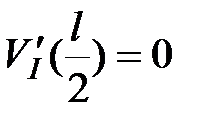
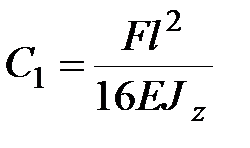
(14.1)

На левой опоре прогиб равен нулю;

,

,

.

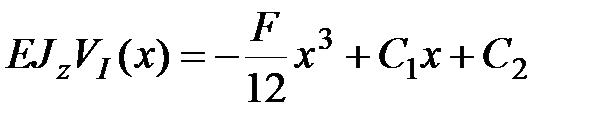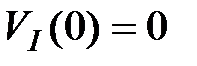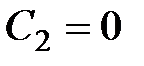(14.2)

Окончательно:

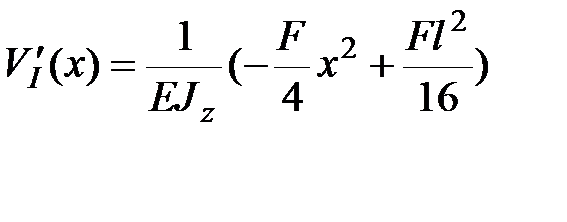
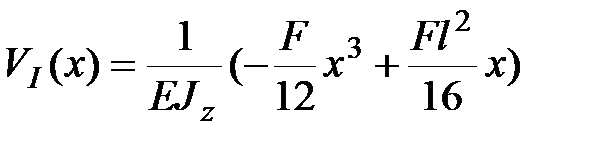
(14.3)

14.2. Решение дифференциальных уравнений оси изогнутой балки способом выравнивания постоянных интегрирования.

Определяем опорные реакции в балке от действия нормативных нагрузок.

Задаемся общим для всех участков загружения началом координат 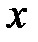, на левом конце балки или на правом . На каждом участке составляем дифференциальное уравнение оси изогнутой балки

,

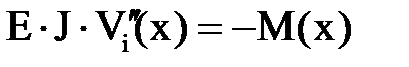(14.3)

где 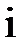– номер участка, 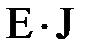– изгибная жесткость балки. Интегрируя дифференциальное уравнение (14.3), получим уравнение тангенсов углов наклона касательной к оси изогнутой балки (углов поворота сечений)

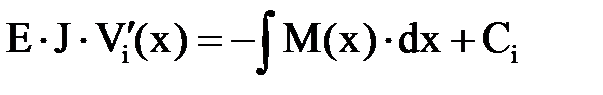
(14.4)

а, интегрируя второй раз, – уравнение прогибов

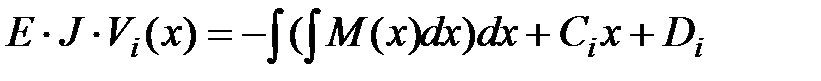
(14.5)

Здесь 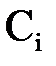и 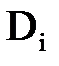– постоянные интегрирования.

Для обеспечения равенства постоянных интегрирования ( 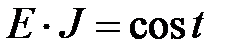) на всех участках загружения 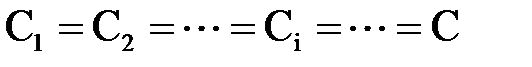и 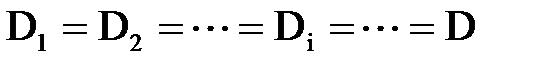необходимо руководствоваться следующими правилами:

1. При составлении выражения для изгибающего момента 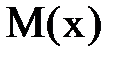всегда рассматривать часть балки, расположенную между началом координат и сечением.

2. Распределенную нагрузку, которая заканчивается на границе участков загружения, продолжать до конца балки с добавлением «компенсирующей» нагрузки противоположного направления («продленную» и «компенсирующие» нагрузки показывать на чертежах штриховыми линиями).

3. Момент пары сил, приложенной к балке на границе участка с координатой 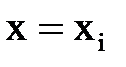, при включении в выражение для изгибающего момента умножать на множитель 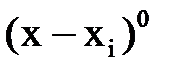, равный единице.

4. Выражения, содержащие множитель вида 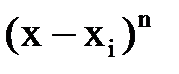, интегрировать, не раскрывая скобок.

Составив и проинтегрировав в соответствии с этими правилами дифференциальные уравнения на каждом участке, необходимо проверить равенство постоянных интегрирования, используя условия гладкого и непрерывного сопряжения оси балки на границах между участками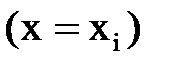

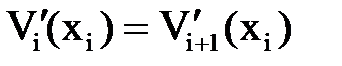
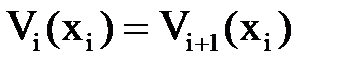
(14.6)

Значения постоянных интегрирования C и D находим из условий равенства нулю прогибов в опорных сечениях для шарнирно опертой балки или прогиба и угла поворота сечения в защемлении для консольной балки.