Принцип действия электронной линзы.
Рассмотрим движение заряженной частицы в электростатическом поле кругового кольца радиуса а с равномерным распределением заряда Q по его длине. Пусть круговое кольцо лежит в плоскости z=0 цилиндрической системы координат  , а начало координат совпадает с центром кольца. Потенциал электростатического поля равномерно заряженного кольца можно рассчитать с использованием принципа суперпозиции
, а начало координат совпадает с центром кольца. Потенциал электростатического поля равномерно заряженного кольца можно рассчитать с использованием принципа суперпозиции
 ,
,  ,
, 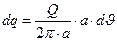 . (1)
. (1)
Декартовы координаты точки наблюдения описываются зависимостями:
 ,
, 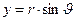 ,
,  . (2)
. (2)
Декартовы координаты расположения «точечного» элементарного заряда  определены соотношениями:
определены соотношениями:
 ,
, 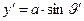 ,
, 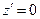 . (3)
. (3)
Зависимости (2) и (3) позволяют вычислить расстояние между точкой наблюдения и положением элементарного заряда 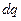 , воспользоваться соотношением (1) и выписать в явном виде интеграл
, воспользоваться соотношением (1) и выписать в явном виде интеграл
 . (4)
. (4)
К сожалению, для произвольной точки наблюдения выражение (4) не может быть получено в элементарных функциях, система символьных вычислений MAPLE позволяет получить в качестве результата следующее выражение:


 (5)
(5)
K(u) – табулированная в математической физике функция – полный эллиптический интеграл первого рода, его использование не представляет труда при использовании математических пакетов символьных вычислений современных компьютеров.
Соотношения (5) позволяют вычислить распределение в пространстве составляющих вектора напряженности электростатического поля:
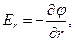
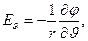
 (6)
(6)
Необходимые результаты получены в разделе 2.2 (формулы (8)-(11) раздела 2.2.6.3):
 , (7)
, (7)
 (8)
(8)
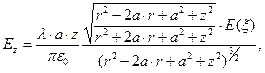 (9)
(9)
где
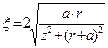 ,
, 

 ,
,  (10)
(10)
Заметим, что в соответствии со структурой совокупности выражений (7)-(9) величина азимутальной составляющей  вектора напряженности электростатического поля обращается в нуль. Рассматривая уравнения классической динамики материальной точки в описанном выше силовом поле (рис. 1)
вектора напряженности электростатического поля обращается в нуль. Рассматривая уравнения классической динамики материальной точки в описанном выше силовом поле (рис. 1)


 (11)
(11)
 приходим к заключению, что если заряженная частица в начальный момент времени не имела угловой скорости
приходим к заключению, что если заряженная частица в начальный момент времени не имела угловой скорости 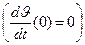 , то величина
, то величина  в процессе движения сохраняет постоянное значение, которое в условиях осевой симметрии физической ситуации можно положить равным нулю. Рассматриваемое движение является не самым общим, но упрощает получение окончательного результата без потери физического смысла.
в процессе движения сохраняет постоянное значение, которое в условиях осевой симметрии физической ситуации можно положить равным нулю. Рассматриваемое движение является не самым общим, но упрощает получение окончательного результата без потери физического смысла.
В практических приложениях (электронная оптика), как правило, рассматривают траектории движения заряженных частиц, близкие к продольной оси системы (параксиальные пучки). Математически условие близости траектории частицы к оси z выражается соотношением r<<a. Раскладывая зависимость для потенциала (5) электростатического поля в ряд Тэйлора по r/a в окрестности нуля и сохраняя члены второго порядка малости, получим:
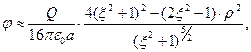
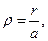
 (12)
(12)
Практическое использование приближённого выражения (12) для потенциала значительно упрощает выкладки. Составляющие напряжённости электростатического поля вблизи оси симметрии системы имеют вид:

 (13)
(13)
Можно проверить, что вычисление соотношений (6) и последующее разложение получаемых результатов в ряд Тэйлора по величине  в окрестности нуля приводит к идентичным зависимостям.
в окрестности нуля приводит к идентичным зависимостям.
Уравнения движения (11) заряженной частицы с учётом приближённых зависимостей (13) можно переписать в «безразмерном» виде:
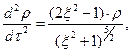


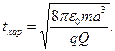 (14)
(14)
Второе из уравнений (14) является нелинейным дифференциальным уравнением второго порядка для функции  и не содержит явно независимую переменную
и не содержит явно независимую переменную 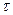 в правой части. В этом случае можно построить его решение в аналитическом виде в форме обратной зависимости
в правой части. В этом случае можно построить его решение в аналитическом виде в форме обратной зависимости 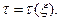 Последующее получение прямой зависимости затруднено из-за сложной структуры обратной зависимости. Более того, далее требуется полученные результаты использовать при решении первого из уравнений (14), надеяться при этом на успех аналитического метода просто не приходится.
Последующее получение прямой зависимости затруднено из-за сложной структуры обратной зависимости. Более того, далее требуется полученные результаты использовать при решении первого из уравнений (14), надеяться при этом на успех аналитического метода просто не приходится.
Решение системы уравнений (14) можно получить численными методами, используя специальное математическое обеспечение современных персональных компьютеров. Начальными условиями движения заряженной частицы являются следующие: начальный момент времени  , начальная радиальная координата частицы
, начальная радиальная координата частицы  , начальная безразмерная скорость частицы в радиальном направлении
, начальная безразмерная скорость частицы в радиальном направлении  , начальная продольная координата частицы
, начальная продольная координата частицы  и начальная безразмерная скорость частицы в продольном направлении
и начальная безразмерная скорость частицы в продольном направлении  . В пакетах символьных вычислений решение рассматриваемой системы дифференциальных уравнений с заданными начальными условиями приводит к получению зависимостей
. В пакетах символьных вычислений решение рассматриваемой системы дифференциальных уравнений с заданными начальными условиями приводит к получению зависимостей
 ,
,  . (15)
. (15)
При записи зависимостей (15) независимая переменная 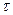 отделена от входных параметров задачи точкой с запятой.
отделена от входных параметров задачи точкой с запятой.
 Физический смысл безразмерных скоростей частицы в радиальном и продольном направлениях определяется с помощью соотношений:
Физический смысл безразмерных скоростей частицы в радиальном и продольном направлениях определяется с помощью соотношений:

 (16)
(16)
На рис. 2. приведены результаты расчёта семейства параксиальных траекторий заряженной частицы в электростатическом поле кругового кольца с равномерно распределённым зарядом. Частица с малым начальным радиальным отклонением от продольной оси ( 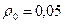 ) начинает двигаться в продольном направлении с безразмерной начальной скоростью
) начинает двигаться в продольном направлении с безразмерной начальной скоростью  =(0,25; 0,50; 0,75, 1,00, 1,50). Чем больше значение величины
=(0,25; 0,50; 0,75, 1,00, 1,50). Чем больше значение величины  , тем «выше» траектория частицы. Легко видеть, что частицы с большой начальной скоростью в продольном направлении «пролетают» управляющее кольцо с относительно малым отклонением траектории к оси симметрии системы. Частицы с малой начальной скоростью в продольном направлении большее время испытывают радиальное воздействие управляющего поля, их траектории сильнее отклоняются в поперечном направлении.
, тем «выше» траектория частицы. Легко видеть, что частицы с большой начальной скоростью в продольном направлении «пролетают» управляющее кольцо с относительно малым отклонением траектории к оси симметрии системы. Частицы с малой начальной скоростью в продольном направлении большее время испытывают радиальное воздействие управляющего поля, их траектории сильнее отклоняются в поперечном направлении.
Осесимметричные фокусирующие поля находят практическое применение в электронной оптике. Теория электронно-оптических систем - фокусирование электронного пучка, получение качественного изображения (электронный микроскоп), измерительные приборы - хорошо разработана и служит надёжной основой создания совершенных приборов и устройств с минимальными значениями аберраций.

На рис. 3 показана принципиальная схема электростатической линзы из двух соосных круговых проводящих цилиндров одного радиуса, находящихся под действием разных потенциалов U1 и U2, причём U2 > U1. Малый промежуток между торцевыми сечениями цилиндров формирует неоднородное электростатическое поле в рассматриваемой области пространства. На рисунке показано качественное расположение эквипотенциальных поверхностей (синие линии), вертикальными стрелками показано направление радиальной силы, действующей на электрон, и две траектории электронов, вылетающих из точки Р1 на оси симметрии системы под разными углами с одинаковыми значениями начальной скорости. Описанные электроны снова пересекают ось симметрии в точке Р2 . Эти точки можно уподобить точкам фокусов оптической системы. Распределение потенциала электростатического поля на оси симметрии системы имеет вид:
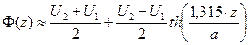 , (17)
, (17)
где а - радиус поперечного сечения цилиндров. Если электрон не имел азимутальной скорости в начале движения, то его движение остаётся плоским, а уравнение траектории можно записать в следующей форме:
 . (18)
. (18)
Решение уравнения (18) зависит от значений начального смещения электрона  и угла наклона траектории в рассматриваемой точке
и угла наклона траектории в рассматриваемой точке  и может быть получено с помощью пакетов специального математического обеспечения современных персональных компьютеров.
и может быть получено с помощью пакетов специального математического обеспечения современных персональных компьютеров.


На рис. 4 показано семейство траекторий электронов, имеющих в сечении 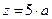 нулевой наклон траектории и разное безразмерное радиальное смещение
нулевой наклон траектории и разное безразмерное радиальное смещение 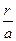 . Здесь же показано в уменьшенном масштабе распределение потенциала
. Здесь же показано в уменьшенном масштабе распределение потенциала  вдоль оси симметрии системы. Легко видеть наличие двух точек Р1 и Р2 на оси симметрии, в которых электроны «собираются» как в фокусах.
вдоль оси симметрии системы. Легко видеть наличие двух точек Р1 и Р2 на оси симметрии, в которых электроны «собираются» как в фокусах.
Электростатические линзы довольно разнообразны по своему устройству. Так фокусирующими свойствами обладает одиночная диафрагма в бесконечной проводящей плоскости и система из трёх соосных диафрагм, средняя из которых имеет отрицательный потенциал, а две крайние – одинаковый положительный потенциал (собирающая линза для электронов с одинаковыми фокусными расстояниями справа и слева от линзы).
Дата добавления: 2017-09-01; просмотров: 1091;










