Векторный потенциал магнитного поля.

Из теоремы Гаусса для векторного поля 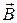в дифференциальной форме 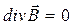следует, что поле 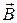можно представить в виде ротора вспомогательного векторного поля 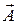, называемого векторным потенциалом:

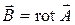, (1)

поскольку 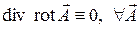. Заметим, что описываемая возможность проявляется и при анализе закона Био-Савара-Лапласа (уравнение 2 из раздела 6.1) с учётом соотношения (7) раздела 6.4. Это естественно, поскольку теорема Гаусса для векторного поля магнитной индукции является следствием закона Био-Савара-Лапласа. Физический смысл в магнитостатике приписывают векторному полю 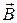, поэтому векторный потенциал, вообще говоря, определен с точностью до градиента любой скалярной функции. Действительно, если 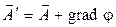, где 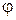- скалярное поле, и 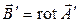, то имеем: 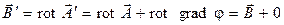, то есть 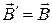для 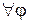, поскольку 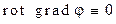. Произвол в определении векторного потенциала 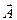можно использовать, потребовав дополнительно выполнения условия

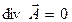. (2)

Условие (2) называют “кулоновской калибровкой векторного потенциала магнитного поля”. Условие (2) влечет за собой далеко идущие последствия, поэтому весьма важным является вопрос, во всех ли случаях магнитное поле обладает указанными свойствами. Пусть выполнено условие

, .

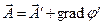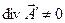Потребуем выполнения условия (2):

.

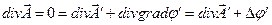Для искомой скалярной функции 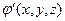получено уравнение Пуассона с известной правой частью. Если рассмотреть его в безграничном пространстве и использовать однородные граничные условия первого рода на бесконечности для искомой функции, то по аналогии с одним из основных результатов электростатики

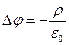
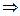
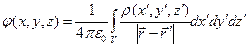
можно записать

.

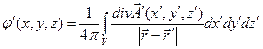Таким образом, показано, что кулоновская калибровка векторного потенциала выполнима в условиях магнитостатики. Её практическое использование требует известной осторожности: если кулоновская калибровка векторного потенциала применяется, надо проследить её выполнение последовательно во всех математических соотношениях задачи, описывающих реальную физическую ситуацию.

Из закона Био-Савара-Лапласа и соотношения (4) раздела 6.1 следует, что магнитное поле, образованное отдельным точечным электрическим зарядом 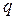, движущимся с постоянной скоростью 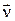, имеет вид:

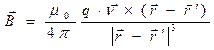. (2)

Здесь 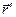- радиус-вектор мгновенного положения электрического заряда, 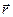- радиус-вектор произвольной точки пространства, разность 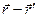является вектором, проведённым из конца вектора 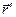(т.е. из точки расположения заряда) в конец вектора 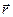(т.е. в описываемую точку пространства).

Векторный потенциал такого поля можно описать выражением:

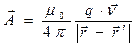. (3)

В современной магнитостатике не существует методики вывода выражения (3), его необходимо просто угадать, но зато можно проверить:

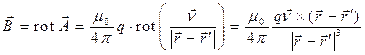. (4)

Напомним читателю, что операция rot в соотношениях (4) выполняется по нештрихованным переменным, т.е. по координатам произвольной точки пространства. Сравнивая между собой выражение (3) для векторного потенциала и выражение для скалярного потенциала электростатического поля отдельного точечного электрического заряда

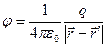, (5)

получаем зависимость:

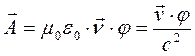. (6)

Зависимость (6) имеет глубокий физический смысл: электростатика и магнитостатика являются внутренне связанными между собой, не надо думать, что они полностью независимы друг от друга.

Из соотношений (5) и (3) можно получить:

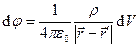, (7)

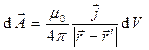, (8)

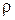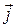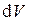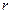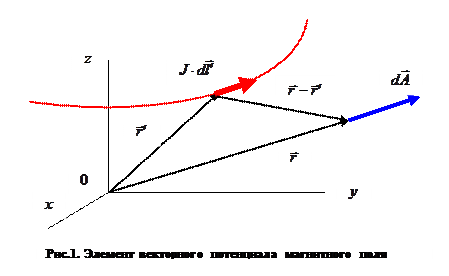
где - объемная плотность электрического заряда, - вектор объемной плотности тока, - элемент объема, - расстояние между элементом объёма 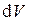и точкой наблюдения. Если электрический ток течёт по тонкому проводнику, элемент кривой линии с током генерирует в окружающем пространстве элемент векторного потенциала (рис. 1):

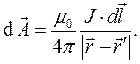(9)

Здесь следует обратить внимание на параллельность направления отрезка проводника с током и элемента векторного потенциала магнитного поля.

Кроме того, обращает на себя внимание идентичность форм записи выражений (7) и (8), особенно, если последнее рассматривать в координатной форме.

Но если для потенциала электростатического поля 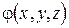справедливо уравнение Пуассона

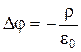, (10)

то для поля векторного потенциала 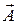должно иметь место аналогичное уравнение:

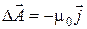. (11)

Мы ещё раз убеждаемся в существовании глубокой аналогии между электрическим и магнитным полем, хотя постараемся помнить, что эта аналогия не стирает полностью различий между ними. Отметим также, что уравнение (11) справедливо при условии, что кулоновская калибровка векторного потенциала выполнена.

Понятием векторного потенциала магнитного поля можно пользоваться для расчёта магнитного поля, образованного заданной системой стационарных электрических токов.