Энергия электростатического поля.

Объёмная плотность электрической энергии. Воспользуемся обобщением выражения для энергии взаимодействия электрических зарядов на случай системы с распределёнными по объёму тела 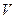электрическими зарядами:

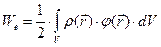, (1)

где 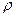- объёмная плотность электрических зарядов

Выражение (1) позволяет записать формулу для электрической энергии через «полевые» переменные, не используя при этом явно величину и пространственное распределение электрических зарядов. В соответствии с теоремой Гаусса для вектора 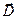в дифференциальной форме

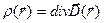(2)

и известным тождеством векторного анализа

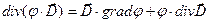(3)

перепишем соотношение (1) в форме:

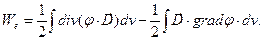(4)

Введение в число используемых соотношений вектора 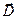означает, что под величиной 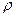мы понимаем объёмную плотность свободных электрических зарядов.

Первое слагаемое формулы (4) можно преобразовать: интеграл по объёму можно заменить интегралом по замкнутой поверхности:

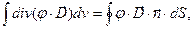(5)

а во втором слагаемом использовать зависимость вектора напряженности электрического поля от градиента потенциала

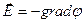. (6)

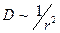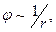
Если электрическое поле образовано зарядами, расположенными в конечной области пространства, а поверхностный интеграл (5) рассматривают по бесконечно удалённой поверхности, то величина этого интеграла обращается в нуль (при больших значениях r имеем оценки , 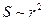). В этих условиях электрическая энергия описывается соотношением:

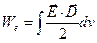. (7)

Подынтегральная функция в выражении (7) представляет собой объёмную плотность электрической энергии в вакууме, т.е. энергию, отнесенную к единице объёма:

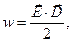
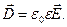(8)

Заметим, что объёмная плотность электрической энергии определена как локальная физическая величина, она может быть не равна нулю и в области пространства, в которой нет электрических зарядов! Достаточно существования «поля», т.е. напряженности электрического поля. Заметим, однако, что по физическому смыслу начальных предпосылок отсутствие электрических зарядов в рассматриваемом объёме должно приводить к нулевой энергии электрического поля в рассматриваемом объёме. Поэтому приведенные рассуждения нельзя считать убедительным доказательством правильности результата. Строгое рассмотрение вопроса об энергии электромагнитного поля можно провести только с помощью системы уравнений Максвелла (теорема Пойнтинга). Это будет сделано ниже в заключительных разделах курса.

Как мы видим, «полевая» трактовка электростатики и трактовка, основанная на главенствующей роли электрических зарядов, существенно различаются между собой.

Электрическая энергия поляризованной среды. В диэлектрической среде вектор 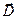определен соотношением

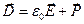, (9)

где 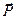- поляризованность (вектор поляризации) среды. Если предположить, что соотношение (1) остаётся в силе, хотя прямых оснований для этого у нас нет, то можно надеяться, что выражение (8) и в рассматриваемом случае правильно описывает величину электрической энергии, запасенной в единице объёма диэлектрической среды. В нестационарной классической электродинамике строго доказано (об этом речь в последующих разделах курса), что совокупность обсуждаемых соотношений действительно описывает объёмную плотность электрической энергии в диэлектрической среде при наличии электрического поля.

Соотношение (9) позволяет выделить в объёмной плотности электрической энергии плотность энергии «пустого» объёма и плотности энергии, связанной с поляризацией среды:

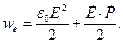(10)

Суммарная электрическая энергия в электростатике определяется зависимостью

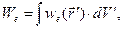(11)

где интегрирование распространяется на весь объём, в котором отлична от нуля подынтегральная функция.

Термодинамический смысл энергии 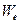. Запасённая в диэлектрической среде энергия может быть обращена в работу, причем соотношением (11) определена максимально возможная величина совершаемой работы при условии, что диэлектрик не нагревается, т.е. в изотермическом процессе. В термодинамике максимальная работа, которую можно получить от системы в изотермическом процессе, называется свободной энергией системы 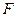. Подчеркнем, что 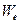непосредственно вносит вклад в свободную энергию системы 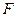, а не во внутреннюю энергию 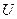. С термодинамической точки зрения напряженность электрического поля 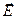соответствует давлению газа, а вектор 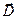- его объёму. При этом имеют место соотношения:

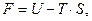
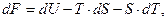
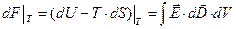. (12)

Здесь 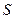- энтропия системы. При практическом использовании формул (12) необходимо иметь в виду, что диэлектрическая проницаемость среды в стационарных условиях является функцией абсолютной температуры.