Теорема Гаусса для вектора поляризованности среды.

Поляризованность среды (вектор поляризации) 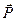обладает примечательным свойством: поток вектора поляризованности среды через произвольную замкнутую поверхность численно равен величине некомпенсированных “связанных” зарядов внутри этой поверхности, взятой с обратным знаком:

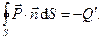(1)

В локальной формулировке описываемое свойство приводит к соотношению

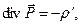(2)

где 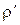- объемная плотность “связанных” зарядов. Соотношения (1) и (2) называют теоремой Гаусса для поляризованности среды (вектора поляризации) в интегральной и дифференциальной формах соответственно. Если теорема Гаусса для напряженности 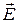электростатического поля является следствием закона Кулона в “полевой” форме, то теорема Гаусса для поляризованности 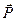является следствием определения этой величины - зависимости (4) - (5) предыдущего раздела.

Докажем соотношение (1), тогда соотношение (2) окажется справедливым в силу математической теоремы Остроградского-Гаусса.

Рассмотрим диэлектрик из неполярных молекул с объемной концентрацией, равной 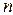. Считаем, что под действием электрического поля положительные заряды сместились из положения равновесия на величину 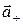, а отрицательные - на величину 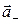. Каждая молекула приобрела электрический момент 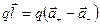, а единичный объем приобрел электрический момент 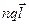. В соответствии с определением поляризованности среды имеет место соотношение 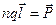. Ниже воспользуемся этим результатом.

Рассмотрим произвольную достаточно гладкую замкнутую поверхн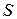ость в описываемом диэлектрике. Допустим, что поверхность 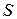проведена так, что в отсутствие электрического поля 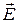она “не пересекает” отдельные диполи, то есть положительный и отрицательный заряды, связанные с молекулярной структурой вещества, полностью “компенсируют” друг друга.

Заметим, кстати, что соотношения (1) и (2) пр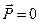и и 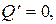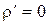удовлетворяются тождественно.

Под действием электрического поля элемент площади поверхности 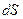(рис. 1) пересекут положительные заряды из объема 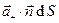в количестве 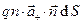. Для отрицательных зарядов имеем соответственно величины 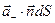и 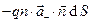. Суммарный заряд, перешедший на “внешнюю” сторону элемента площади поверхности 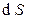(напомним, что 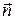- внешняя нормаль к 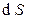по отношению к охватываемому поверхностью 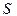объему), равен

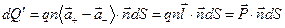. (3)

Проинтегрировав выражение (3) по замкнутой поверхности 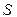, получим величину суммарного электрического заряда, покинувшего рассматриваемый объем. Последнее позволяет заключить, что в рассматриваемом объеме остался некомпенсированный заряд - 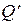, равный по модулю ушедшему заряду. В итоге имеем:

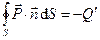, (4)

таким образом, теорема Гаусса для векторного поля 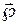в интегральной формулировке доказана. Чтобы рассмотреть случай вещества, состоящего из полярных молекул, достаточно в приведенных выше рассуждениях величину 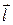заменить на ее среднее значение 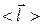. Доказательство справедливости интегрального соотношения (1) можно считать законченным. Дифференциальное (локальное) соотношение (2) является математическим следствием теоремы Остроградского-Гаусса.