ФРАКТАЛЫ И МИР ВОКРУГ НАС

Фракталы - уникальные объекты, порожденные непредсказуемыми движениями хаотического мира. Их находят в местах таких малых, как клеточная мембрана и таких огромных, как Солнечная система.

Разветвления трубочек трахей, листья на деревьях, вены в руке, река, бурлящая и изгибающаяся, рынок ценных бумаг — это все фракталы. От представителей древних цивилизаций до Майкла Джексона, ученые, математики и артисты, как и все остальные обитатели этой планеты, были зачарованы фракталами и применяли из в своей работе.

Программисты и специалисты в области компьютерной техники так же без ума от фракталов, так как фракталы бесконечной сложности и красоты могут быть сгенерированы простыми формулами на простых домашних компьютерах. Открытие фракталов было открытием новой эстетики искусства, науки и математики, а так же революцией в человеческом восприятии мира.

ЧТО ЖЕ ТАКОЕ ФРАКТАЛЫ НА САМОМ ДЕЛЕ?

Слово “Фрактал” — это что-то, о чем много людей говорит в наши дни, от физиков до учеников средней школы. Оно появляется на обложках многих учебников математики, научных журналов и коробках с компьютерным программным обеспечением. Цветные картинки фракталов сегодня можно найти везде: от открыток до футболок. За последние два десятка лет количество производимых в месяц единиц продукции, связанной с фракталами, увеличилось от нескольких десятков до многих тысяч!

Итак, что это за цветные формы, которые мы видим повсюду вокруг? Говоря простым языком, фрактал — это геометрическая фигура, определенная часть которой повторяется снова и снова, изменяясь в размерах. Отсюда следует принцип самоподобия. Все фракталы подобны самим себе, то есть они похожи на всех уровнях. Существует много типов фракталов, причем здесь описываются довольно большое их количество.

Однако фракталы — не просто сложные фигуры, сгенерированные компьютерами. Все, что кажется случайным и неправильным может быть фракталом. Теоретически, можно сказать, что все что существует в реальном мире является фракталом, будь то облако или маленькая молекула кислорода.

НАСКОЛЬКО ХАОТИЧЕН ХАОС?

Фракталы всегда ассоциируются со словом хаос. Я лично, определил бы фракталы, как частички хаоса. Фракталы проявляют хаотическое поведение, благодаря которому они кажутся такими беспорядочными и случайными. Но если взглянуть достаточно близко, можно увидеть много аспектов самоподобия внутри фрактала. Например, посмотрите на дерево, затем выберите определенную ветку и изучите ее поближе. Теперь выберите связку из нескольких листьев. Для ученых, занимающихся фракталами (которых иногда называют хаологами), все эти три объекта представляются идентичными.

Слово хаос наводит большинство людей на мысли о чем-то беспорядочном и непредсказуемом. На самом деле, это не совсем так. Итак насколько хаотичен хаос? Ответ таков, что хаос, в действительности, достаточно упорядочен и подчиняется определенным законам. Проблема состоит в том, что отыскание этих законов может быть очень сложным. Цель изучения хаоса и фракталов — предсказать закономерность в системах, которые могут казаться непредсказуемыми и абсолютно хаотическими.

Система — это набор вещей, или область изучения, причем некоторые из обычных систем, которые хаологи любят изучать включают облачные образования, погода, движение водных потоков, миграции животных, и множество других аспектов из жизни природы. Так что, в конце концов, может быть, весь мир вокруг нас фрактален!

ГЕОМЕТРИЯ 21 ВЕКА

Для многих хаологов, изучение хаоса и фракталов не просто новая область познания, которая объединяет математику, теоретическую физику, искусство и компьютерные технологии — это революция. Это открытие нового типа геометрии, той геометрии, которая описывает мир вокруг нас и которую можно увидеть не только в учебниках, но и в природе и везде в безграничной вселенной.

Пионером в этой новой области познания, которого многие называют отцом фракталов был Франко-Американский математик Профессор Бенуа Б. Мандельброт (Benoit B. Mandelbrot). В середине 1960х после десятилетий обучения и научной деятельности, Мандельброт разработал то, что он назвал фрактальная геометрия или геометрия природы (об этом он написал свой бестселлер — Фрактальная геометрия природы). Целью фрактальной геометрии был анализ сломанных, морщинистых и нечетких форм. Мандельброт использовал слово фрактал, потому что это предполагало осколочность и фракционность этих форм.

Сегодня Мандельброт и другие ученые, такие как Клиффорд А. Пикковер (Clifford A. Pickover), Джеймс Глейк (James Gleick) или Г. О. Пейтген (H.O. Peitgen) пытаются расширить область фрактальной геометрии так, чтобы она могла быть применена практически ко всему в мире, от предсказания цен на рынке ценных бумаг до совершения новых открытий в теоретической физике.

ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ФРАКТАЛОВ

Фракталы находят все большее и большее применение в науке. Основная причина этого заключается в том, что они описывают реальный мир иногда даже лучше, чем традиционная физика или математика. Вот несколько примеров:

КОМПЬЮТЕРНЫЕ СИСТЕМЫ

Наиболее полезным использованием фракталов в компьютерной науке является фрактальное сжатие данных. В основе этого вида сжатия лежит тот факт, что реальный мир хорошо описывается фрактальной геометрией. При этом, картинки сжимаются гораздо лучше, чем это делается обычными методами (такими как jpeg или gif). Другое преимущество фрактального сжатия в том, что при увеличении картинки, не наблюдается эффекта пикселизации (увеличения размеров точек до размеров, искажающих изображение). При фрактальном же сжатии, после увеличения, картинка часто выглядит даже лучше, чем до него.

МЕХАНИКА ЖИДКОСТЕЙ

Изучение турбулентности в потоках очень хорошо подстраивается под фракталы. Турбулентные потоки хаотичны и поэтому их сложно точно смоделировать. И здесь помогает переход к из фрактальному представлению, что сильно облегчает работу инженерам и физикам, позволяя им лучше понять динамику сложных потоков.

При помощи фракталов также можно смоделировать языки пламени.

Пористые материалы хорошо представляются в фрактальной форме в связи с тем, что они имеют очень сложную геометрию. Это используется в нефтяной науке.

ТЕЛЕКОММУНИКАЦИИ

Для передачи данных на расстояния используются антенны, имеющие фрактальные формы, что сильно уменьшает их размеры и вес.

ФИЗИКА ПОВЕРХНОСТЕЙ

Фракталы используются для описания кривизны поверхностей. Неровная поверхность характеризуется комбинацией из двух разных фракталов.

МЕДИЦИНА

Биосенсорные взаимодействия

Биения сердца

БИОЛОГИЯ

Моделирование хаотических процессов, в частности при описании моделей популяций.

ФРАКТАЛЬНАЯ РАЗМЕРНОСТЬ: СПРЯТАННЫЕ ИЗМЕРЕНИЯ

Одной из идей, выросших из открытия фрактальной геометрии была идея нецелых значений для количества измерений в пространстве. Конечно, мы не можем осознать четырехмерные вещи, хотя Lucky Tesseract и активно работает в этом направлении. Мандельброт назвал нецелые измерения такие как 2.76 фрактальными измерениями. Обыкновенная евклидова геометрия утверждает, что пространство ровное и плоское. Свойства такого пространства такого пространства задают точки, линии, углы, треугольники, кубы, сферы, тетраэдры и т. д.

Мандельброт верил, что действительный ландшафт пространства не ровный и что в нашем мире нет ничего, что было бы совершенно плоским, круглым, то есть все фрактально. Следовательно объект, имеющий точно 3 измерения невозможен. Вот почему концепция фрактального измерения была нужна для измерения степени неровности вещей.

Например посмотрите на лист бумаги (предположим, что он двумерный), скомканный в шар. Разве он двумерный? Нет, так как у него есть длина, ширина и высота. Но он не может быть и трехмерным, потому что он сделан из одного бесконечно тонкого листа и, к тому же, он не полностью однородный. Итак, его фрактальная размерность приблизительно равна 2.5. Но его нормальная размерность, так же называемая Евклидовой размерностью будет равна 3. Все фракталы, особенно фрактальные кривые, имеют фрактальные размерности. Мандельброт часто использовал пример того, что береговая линия Англии имеет бесконечную длину.

Попытайтесь наложить нитку на береговую линии Англии на атласе. Затем сделайте то же самое с мореходной картой. Удивительно, но величина последнего измерения будет гораздо больше. Затем поезжайте в Англию и измерьте ее береговую линию метровой полкой. Эта длина будет еще длинней. Продолжайте этот процесс до тех пор, пока у вас в руках не окажется чертежная линейка, которой вы можете измерить береговую линию частичка за частичкой, атом за атомом. Конечно идея этого непрактичного эксперимента в том, что расстояния должны быть соизмеримы по масштабу, положению и деталям. Позже Мандельброт определил, что фрактальная размерность береговой линии Англии составляет 1.25.

Многие объекты в природе (например человеческое тело) состоят из множества фракталов, смешанных друг с другом, причем каждый фрактал имеет свою размерность отличную от размерности остальных. Например, двумерная поверхность человеческой сосудистой системы изгибается, ветвится, скручивается и сжимается так, что ее фрактальная размерность равна 3.0. Но если бы она была разделена на отдельные части, фрактальная размерность артерий была бы только 2.7, тогда как бронхиальные пути в легких имели бы фрактальную размерность 1.07.

РАЗДЕЛ 2: ДЕТЕРМИНИРОВАННЫЕ ФРАКТАЛЫ

ОБЩАЯ ХАРАКТЕРИСТИКА

Первыми открытыми фракталами были т.н. детерминированные фракталы. Их отличительной чертой является свойство самоподобия, обусловленное особенностями метода их генерации.

Некоторые предпочитают называть эти фракталы классическими, геометрическими фракталами или линейными фракталами. Эти фракталы обычно формируются начиная с инициатора — фигуры, к которой применяется определенный основной рисунок. Во всех детерминированных фракталах, само-подобие проявляется на всех уровнях. Это значит, что независимо от того насколько вы приближаете фрактал, вы увидите все тот же узор. Для сложных фракталов, которые будут рассмотрены позже, это не так. Детерминистские фракталы образуются в процессе, называемом итерацией, которая применяет основной рисунок к инициатору, после чего применяет его к результату и так далее. Большинство людей итерируют детерминированные фракталы 5-7 раз чтобы получить четкую красивую картинку. Эти фракталы линейны, так как при каждой итерации, что-то убирается либо прибавляется в форме прямых линий. Ниже находятся примеры некоторых обычных детерминированных фракталов, сгенерированных на обычном компьютере простыми программами на BASIC’е.

РЕШЕТКА СЕРПИНСКОГО

Это один из фракталов, с которыми экспериментировал Мандельброт, когда разрабатывал концепции фрактальных размерностей и итераций. Треугольники, сформированные соединением средних точек большего треугольника вырезаны из главного треугольника, образовывая треугольник, с большим количеством дырочек. В этом случае инициатор — большой треугольник а шаблон — операция вырезания треугольников, подобных большему. Так же можно получить и трехмерную версию треугольника, используя обыкновенный тетраэдр и вырезая маленькие тетраэдры. Размерность такого фрактала ln3/ln2 = 1.584962501.

Чтобы получить ковер Серпинского, возьмем квадрат, разделим его на девять квадратов, а средний вырежем. То же сделаем и с остальными, меньшими квадратами. В конце концов образуется плоская фрактальная сетка, не имеющая площади, но с бесконечными связями. В своей пространственной форме, губка Серпинского преобразуется в систему сквозных форм, в которой каждый сквозной элемент постоянно заменяется себе подобным. Эта структура очень похожа на разрез костной ткани. Когда-нибудь такие повторяющиеся структуры станут элементом строительных конструкций. Их статика и динамика, считает Мандельброт, заслуживает пристального изучения.

ФРАКТАЛ СЕРПИНСКОГО

Не перепутайте этот фрактал с решеткой Серпинского. Это два абсолютно разных объекта. В этом фрактале, инициатор и генератор одинаковы. При каждой итерации, добавляется уменьшенная копия инициатора к каждому углу генератора и так далее. Если при создании этого фрактала произвести бесконечное число итераций, он бы занял всю плоскость, не оставив ни одной дырочки. Поэтому его фрактальная размерность ln9/ln3 = 2.0

КРИВАЯ КОХА

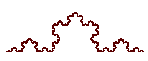
Кривая Коха один из самых типичных детерминированных фракталов. Она была изобретена в девятнадцатом веке немецким математиком по имени Хельге фон Кох, который, изучая работы Георга Контора и Карла Вейерштрассе, натолкнулся на описания некоторых странных кривых с необычным поведением. Инициатор — прямая линия. Генератор — равносторонний треугольник, стороны которого равны трети длины большего отрезка. Эти треугольники добавляются к середине каждого сегмента снова и снова. В своем исследовании, Мандельброт много экспериментировал с кривыми Коха, и получил фигуры такие как Острова Коха, Кресты Коха, Снежинки Коха и даже трехмерные представления кривой Коха, используя тетраэдр и прибавляя меньшие по размерам тетраэдры к каждой его грани. Кривая Коха имеет размерность ln4/ln3 = 1.261859507.

Крест Коха — это один из вариантов кривой Коха, изобретенный Мандельбротом. Вместо отрезка прямой, он использовал в качестве инициатора квадрат или прямоугольник. Так как в этом фрактале использован та же самая идея что и в оригинальной кривой Коха, его фрактальная размерность такая же: ln4/ln3 = 1.261859507.

ФРАКТАЛ МАНДЕЛЬБРОТА

Это НЕ множество Мандельброта, которое можно достаточно часто видеть. Множество Мандельброта основано на нелинейных уравнениях и является комплексным фракталом. Это тоже вариант кривой Коха несмотря на то, что этот объект не похож на нее. Инициатор и генератор так же отличны от использованных для создания фракталов, основанных на принципе кривой Коха, но идея остается той же. Вместо того, чтобы присоединять равносторонние треугольники к отрезку кривой, квадраты присоединяются к квадрату. Благодаря тому, что этот фрактал занимает точно половину отведенного пространства при каждой итерации, он имеет простую фрактальную размерность 3/2 = 1.5

ФРАКТАЛЫ ЗВЕЗДА И СНЕЖИНКА

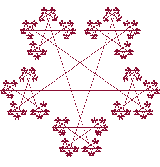
Оба эти объекта не являются классическими фракталами и они не были изобретены Мандельбротом или кем-либо из известных математиков. Я просто создал эти фракталы из интереса и чтобы поэкспериментировать в программировании. И инициатор и генератор здесь фигура, сформированная соединением средних точек сторон со средними точками противолежащих сторон в правильном шестиугольнике. Более того, я могу только подозревать о размерности этих фракталов.

КОЛБАСА МИНКОВСКОГО

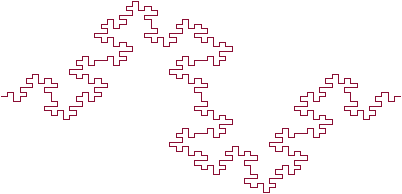
Автор этого фрактала Герман Минковский, по имени которого он и был назван. Минковский не предлагал термин колбаса для названия этого объекта. Слово кривая или просто фрактал, возможно, понравилось бы больше. И инициатор и генератор довольно сложны и составлены из ряда прямых углов и сегментов различной длины. У самого инициатора 8 частей. Фрактальная размерность колбасы Минковского — ln8/ln4 = 1.5

ФРАКТАЛ ЛАБИРИНТ

Этот фрактал еще иногда называют H-деревом. И инициатор и генератор имеют вид буквы H. На приведенном здесь примере сама H не закрашена. Вместо этого заполнены области вне фрактала, что облегчает восприятие рисунка и шаблона. Фрактальная размерность этого конкретно фрактала весьма интересна. Так как толщина H в процессе итераций уменьшается, размерность кончиков буквы H точно 2.0, но элементы между кончиками имеют другую размерность, меняющуюся от 1.3333 до 1.6667.

ПЯТИУГОЛЬНИК ДАРЕРА

Фрактал выглядит как связка пятиугольников, сжатых вместе. Фактически он образован при использовании пятиугольника в качестве инициатора и равнобедренных треугольников, отношение большей стороны к меньшей в которых в точности равно так называемой золотой пропорции (1.618033989 или 1/(2cos72)) в качестве генератора. Эти треугольники вырезаются из середины каждого пятиугольника, в результате чего получается фигура, похожая на 5 маленьких пятиугольников, приклеенных к одному большому.

Вариант этого фрактала можно получить при использовании в качестве инициатора шестиугольника. Этот фрактал называется Звезда Давида и он довольно похож на шестиугольную версию Снежинки Коха. Фрактальная размерность пятиугольника Дарера ln6/ln(1+g), где g — отношение длины большей стороны треугольника к длине меньшей. В данном случае, g — это Золотая Пропорция, так что фрактальная размерность приблизительно равна 1.86171596. Фрактальное измерение Звезды Давида ln6/ln3 или 1.630929754.

КРИВАЯ ДРАКОНА

Изобретенная итальянским математиком Джузеппе Пеано, Кривая Дракона или Взмах Дракона, как он назвал его, очень похож на колбасу Минковского. Использован более простой инициатор, а генератор тот же самый. Мандельброт назвал этот фрактал Река Двойного Дракона. Его фрактальная размерность приблизительно равна 1.5236.

КРИВАЯ ГИЛЬБЕРТА

Этот фрактал очень похож на Фрактал Лабиринт, кроме того факта что ширина буквы U, являющейся генератором не изменяется с каждой итерацией. Однако, в отличии от Фрактала Лабиринта, кривая Гильберта также называемая Отелем Гильберта, имеет одно единственное фрактальное измерение, которое точно равно 2.0, так как при бесконечном количестве итераций, он займет всю плоскость.

ФРАКТАЛ КОРОБКА

Это очень простой детерминированный фрактал, который образуется при прибавлении квадратов к вершинам других квадратов. И инициатор и генератор — квадраты. Его фрактальная размерность ln8/ln3 или 1.892789261.

РАЗДЕЛ 3: СЛОЖНЫЕ ФРАКТАЛЫ

ОБЩАЯ ХАРАКТЕРИСТИКА

Большая часть встречающихся сегодня фракталов не являются детерминированными. Они не линейны и не собранны из повторяющихся геометрических форм. Такие фракталы называются сложными.

Фактически, если вы увеличите маленькую область любого сложного фрактала а затем проделаете то же самое с маленькой областью этой области, то эти два увеличения будут значительно отличаться друг от друга. Два изображения будут очень похожи в деталях, но они не будут полностью идентичными.

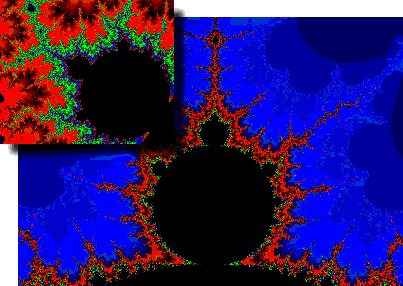
Сравните, например приведенные здесь картинки множества Мандельброта, одна из которых получена при увеличении некоторой области другой. Как видно, они абсолютно не являются идентичными, хотя на обоих мы видим черный круг, от которого в разные стороны идут пылающие щупальца. Эти элементы повторяются бесконечно долго во множестве Мандельброта в уменьшающейся пропорции.

Детерминистские фракталы являются линейными, тогда как сложные фракталы таковыми не являются. Будучи нелинейными, эти фракталы генерируются тем, что Мандельброт назвал нелинейными алгебраическими уравнениями. Хороший пример — это процесс Zn+1=ZnІ + C, что является уравнением, используемым для построения множества Мандельброта и Жулии второй степени. Решение этих математических уравнений вовлекает комплексные и мнимые числа. Когда уравнение интерпретируется графически на комплексной плоскости, результатом оказывается странная фигура, в которой прямые линии переходят в кривые, появляются хотя и не без деформаций, эффекты самоподобия на различных масштабных уровнях. При этом вся картина в целом является непредсказуемой и очень хаотичной.

Как можно увидеть, смотря на картинки, сложные фракталы действительно очень сложны и их невозможно создать без помощи компьютера. Для получения красочных результатов этот компьютер должен обладать мощным математическим сопроцессором и монитором с высоким разрешением. В отличии от детерминистских фракталов, сложные фракталы не вычисляются за 5-10 итераций. Практически каждая точка на экране компьютера как отдельный фрактал. Во время математической обработки, каждая точка рассматривается как отдельный рисунок. Каждой точке соответствует определенное значение. Уравнение встраивается, применительно к каждой точке и производится, к примеру 1000 итераций. Для получения сравнительно неискаженного изображения за приемлемый для домашних компьютеров промежуток времени, для одной точки возможно проводить 250 итерации.

Большинство фракталов, которые мы видим сегодня, красиво раскрашены. Возможно фрактальные изображения получили такое большое эстетическое значение именно благодаря своим цветовым схемам. После того, как уравнение посчитано, компьютер анализирует результаты. Если результаты остаются стабильными, или колеблются вокруг определенного значения, точка обычно принимает черный цвет. Если значение на том или ином шаге стремится к бесконечности, точку закрашивают в другой цвет, может быть в синий или красный. Во время этого процесса, компьютер назначает цвета для всех скоростей движения.

Обычно, быстро движущиеся точки закрашивают в красный цвет, тогда как более медленные в желтый и так далее. Темные точки, вероятно, самые стабильные.

Сложные фракталы отличаются от детерминистских в том смысле, что они бесконечно сложные, но, при этом, могут быть сгенерированы очень простой формулой. Детерминистским фракталам не нужны формулы или уравнения. Просто возьмите чертежную бумагу и вы можете построить решето Серпинского до 3 или 4 итерации без каких-либо затруднений. Попробуйте сделать это с множеством Жулиа! Легче пойти мерить длину береговой линии Англии!

МНОЖЕСТВО МАНДЕЛЬБРОТА

Множества Мандельброта и Жулиа, вероятно, два наиболее распространенных среди сложных фракталов. Их можно найти во многих научных журналах, обложках книг, открытках, и в компьютерных хранителях экрана. Множество Мандельброта, которое было построено Бенуа Мандельбротом, наверное первая ассоциация, возникающая у людей, когда они слышат слово фрактал. Этот фрактал, напоминающий чесальную машину с прикрепленными к ней пылающими древовидными и круглыми областями, генерируется простой формулой Zn+1=Zna+C, где Z и C — комплексные числа и а — положительное число.

Множество Мандельброта, которое чаще всего можно увидеть — это множество Мандельброта 2й степени, то есть а=2. Тот факт, что множество Мандельброта не только Zn+1=ZnІ+C, а фрактал, показатель в формуле которого может быть любым положительным числом ввел в заблуждение многих. На этой странице вы видите пример множества Мандельброта для различных значений показателя а.

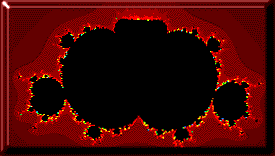
Также популярен процесс Z=Z*tg(Z+C). Благодаря включению функции тангенса, получается множество Мандельброта, окруженное областью, напоминающей яблоко. При использовании функции косинуса, получаются эффекты воздушных пузырьков. Короче говоря, существует бесконечное количество способов настройки множества Мандельброта для получения различных красивых картинок.

МНОЖЕСТВО ЖУЛИА

Удивительно, но множества Жулиа образуются по той же самой формуле, что и множество Мандельброта. Множество Жулиа было изобретено французским математиком Гастоном Жулиа, по имени которого и было названо множество. Первый вопрос, возникающий после визуального знакомства с множествами Мандельброта и Жулиа это “если оба фрактала сгенерированы по одной формуле, почему они такие разные?” Сначала посмотрите на картинки множества Жулиа. Достаточно странно, но существуют разные типы множеств Жулиа. При рисовании фрактала с использованием различных начальных точек (чтобы начать процесс итераций), генерируются различные изображения. Это применимо только ко множеству Жулиа:

Хотя это нельзя увидеть на картинке, фрактал Мандельброта — это, на самом деле, множество фракталов Жулиа, соединенных вместе. Каждая точка (или координата) множества Мандельброта соответствует фракталу Жулиа. Множества Жулиа можно сгенерировать используя эти точки в качестве начальных значений в уравнении Z=ZІ+C. Но это не значит, что если выбрать точку на фрактале Мандельброта и увеличить ее, можно получить фрактал Жулиа. Эти две точки идентичны, но только в математическом смысле. Если взять эту точку и просчитать ее по данной формуле, можно получить фрактал Жулиа, соответствующий определенной точке фрактала Мандельброта.

РАЗДЕЛ 4: ТЕОРИЯ ХАОСА

ЧТО ТАКОЕ ТЕОРИЯ ХАОСА?

Формально, теория хаоса определяется как учение о сложных нелинейных динамических системах. Под термином сложные это и понимается, а под термином нелинейные понимается рекурсия и алгоритмы из высшей математики, и, наконец, динамические — означает непостоянные и непериодические. Таким образом, теория хаоса – это учение о постоянно изменяющихся сложных системах, основанное не математических концепциях рекурсии, в форме ли рекурсивного процесса или набора дифференциальных уравнений, моделирующих физическую систему.

НЕПРАВИЛЬНЫЕ ПРЕДСТАВЛЕНИЯ О ТЕОРИИ ХАОСА

Широкая общественность обратила внимание на теорию хаоса благодаря таким фильмам, как Парк юрского периода, и благодаря им же, постоянно увеличивается опасение теории хаоса со стороны общества. Однако, как и в отношении любой вещи, освещаемой средствами массовой информации, в отношении теории хаоса возникло много неправильных представлений.

ТЕОРИЯ ХАОСА О БЕСПОРЯДКЕ

Наиболее часто встречающееся несоответствие состоит в том, что люди полагают, что теория хаоса — это теория о беспорядке. Ничто не могло бы быть так далеко от истины! Это не опровержение детерминизма и не утверждение о том, что упорядоченные системы невозможны; это не отрицание экспериментальных подтверждений и не заявление о бесполезности сложных систем. Хаос в теории хаоса и есть порядок — и даже не просто порядок, а сущность порядка.

Это правда, что теория хаоса утверждает, что небольшие изменения могут породить огромные последствия. Но одной из центральных концепций в теории является невозможность точного предсказания состояния системы. В общем, задача моделирования общего поведения системы вполне выполнима, даже проста. Таким образом, теория хаоса сосредотачивает усилия не на беспорядке системы — наследственной непредсказуемости системы — а на унаследованном ей порядке — общем в поведении похожих систем.

Таким образом, было бы неправильным сказать, что теория хаоса о беспорядке. Чтобы пояснить это на примере, возьмем аттрактор Лоренца. Он основан на трех дифференциальных уравнениях, трех константах и трех начальных условиях.

Аттрактор представляет поведение газа в любое заданное время, и его состояние в определенный момент зависит от его состояния в моменты времени, предшествовавшие данному. Если исходные данные изменить даже на очень маленькие величины, скажем, эти величины малы настолько, что соизмеримы с колебаниями числа Авогадро (очень маленькое число порядка 1024), проверка состояния аттрактора покажет абсолютно другие числа. Это происходит потому, что маленькие различия увеличиваются в результате рекурсии. Однако, несмотря на это, график аттрактора будет выглядеть достаточно похоже. Обе системы будут иметь абсолютно разные значения в любой заданный момент времени, но график аттрактора останется тем же самым, т.к. он выражает общее поведение системы.

Теория хаоса говорит, что сложные нелинейные системы являются наследственно непредсказуемыми, но, в то же время, теория хаоса утверждает, что способ выражения таких непредсказуемых систем оказывается верным не в точных равенствах, а в представлениях поведения системы — в графиках странных аттракторов или во фракталах. Таким образом, теория хаоса, о которой многие думают как о непредсказуемости, оказывается, в то же время, наукой о предсказуемости даже в наиболее нестабильных системах.

Однако согласно вышесказанному не следует, что теория хаоса не имеет приложений в реальной жизни.

ПРИМЕНЕНИЕ ТЕОРИИ ХАОСА В РЕАЛЬНОМ МИРЕ

При появлении новых теорий, все хотят узнать что же в них хорошего. Итак что хорошего в теории хаоса?

Первое и самое важное — теория хаоса — это теория. А значит, что большая ее часть используется больше как научная основа, нежели как непосредственно применимое знание. Теория хаоса является очень хорошим средством взглянуть на события, происходящие в мире отлично от более традиционного четко детерминистического взгляда, который доминировал в науке со времен Ньютона. Зрители, которые посмотрели Парк Юрского периода, без сомнения боятся, что теория хаоса может очень сильно повлиять на человеческое восприятие мира, и, в действительности, теория хаоса полезна как средство интерпретации научных данных по-новому. Вместо традиционных X-Y графиков, ученые теперь могут интерпретировать фазово-пространственные диаграммы которые — вместо того, чтобы описывать точное положение какой-либо переменной в определенный момент времени — представляют общее поведение системы. Вместо того, чтобы смотреть на точные равенства, основанные на статистических данных, теперь мы можем взглянуть на динамические системы с поведением похожим по своей природе на статические данные — т.е. системы с похожими аттракторами. Теория хаоса обеспечивает прочный каркас для развития научных знаний.

Техники теории хаоса использовались для моделирования биологических систем, которые, бесспорно, являются одними из наиболее хаотических систем из всех что можно себе представить. Системы динамических равенств использовались для моделирования всего — от роста популяций и эпидемий до аритмических сердцебиений.

В действительности, почти любая хаотическая система может быть смоделирована — рынок ценных бумаг порождает кривые, которые можно легко анализировать при помощи странных аттракторов в отличие от точных соотношений; процесс падения капель из протекающего водопроводного крана кажется случайным при анализе невооруженным ухом, но если его изобразить как странный аттрактор, открывается сверхъестественный порядок, которого нельзя было бы ожидать от традиционных средств.

Фракталы находятся везде, наиболее заметны в графических программах как например очень успешная серия продуктов Fractal Design Painter. Техники фрактального сжатия данных все еще разрабатываются, но обещают удивительные результаты как например коэффициента сжатия 600:1. Индустрия специальных эффектов в кино, имела бы горазда менее реалистичные элементы ландшафта (облака, скалы и тени) без технологии фрактальной графики.

И, конечно, теория хаоса дает людям удивительно интересный способ того, как приобрести интерес к математике, одной из наиболее мало-популярной области познания на сегодняшний день.

ДВИЖЕНИЕ БИЛЛИАРДНОГО ШАРИКА

Любой, кто когда либо брал в руки кий для бильярда, знает, что ключ к игре — точность. Малейшая ошибка в угле начального удара может быстро привести к огромной ошибке в положении шарика всего после нескольких столкновений. Эта чувствительность к начальным условиям называемая хаосом возникает непреодолимым барьером для любого, кто надеется предсказать или управлять траекторией движения шарика больше чем после шести или семи столкновений. И не стоит думать, что проблема заключается в пыли на столе или в нетвердой руке. Фактически, если вы используете ваш компьютер для построения модели, содержащей бильярдный стол, не обладающий ни каким трением, нечеловеческим контролем точности позиционирования кия, вам все равно не удастся предсказывать траекторию шарика достаточно долго!

Насколько долго? Это зависит частично от точности вашего компьютера, но в большей степени от формы стола. Для совершенно круглого стола, можно просчитать приблизительно до 500 положений столкновений с ошибкой около 0.1 процента. Но стоит изменить форму стола так, чтобы она стала хотя бы немножко неправильной (овальной), и непредсказуемость траектории может превышать 90 градусов уже после 10 столкновений! Единственный путь получить картинку общего поведения бильярдного шарика, отскакивающего от чистого стола — это изобразить угол отскока или длину дуги соответствующую каждому удару. Здесь приведены два последовательных увеличения такой фазово-пространственной картины.

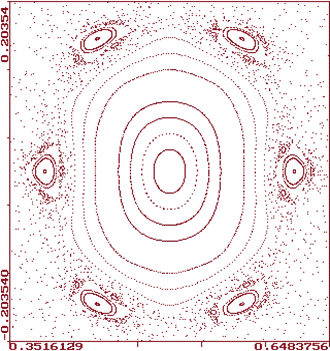
Каждая отдельная петля или область разброса точек представляет поведение шарика, происходящее от одного набора начальных условий. Область картинки, на которой отображаются результаты какого-то одного конкретного эксперимента, называется аттракторной областью для данного набора начальных условий. Как можно видеть форма стола, использованного для этих экспериментов является основной частью аттракторных областей, которые повторяются последовательно в уменьшающемся масштабе. Теоретически, такое самоподобие должно продолжаться вечно и если мы будем увеличивать рисунок все больше и больше, мы бы получали все те же формы. Это называется очень популярным сегодня словом фрактал.

РАЗДЕЛ 5: ДЕРЕВО ФЕЙГЕНБАУМА

ОБЩАЯ ИНФОРМАЦИЯ

Теория хаоса находит прямое применение в задаче моделирования роста популяций и рассматривается здесь на примере диаграммы Фейгенбаума, построенной с помощью программы LT Bifurcator.

БИФУРКАЦИИ В МОДЕЛЯХ ПОПУЛЯЦИЙ

Чудо фрактальной геометрии заключается в том, что чрезвычайно сложные формы могут получаться из таких простых процессов генерирования. Еще один сюрприз преподносит нам учение о динамических системах: такие простые, детерминированные уравнения могут порождать такое хаотическое поведение, при котором система никогда не возвращается в стабильное состояние и не проявляется никакой закономерности. Часто такие системы ведут себя вполне нормально до некоторого определенного значения ключевого параметра, потом испытывают переход и в котором существует две возможности дальнейшего развития, потом четыре, и, наконец, хаотический набор возможностей.

В 1786 году Томас Мальтус разработал математическую модель роста популяций и оказалось, что эта и другие модели подобного типа обладают описанным выше свойством. Предположим, что у нас есть модель в которой скорость роста популяции это функция, в частности, от численности популяции:

Новая популяция = скорость роста * старая популяция (1 – старая популяция)

Где популяция нормализована так, что она принимает значения от 0 до 1. Естественно, такая модель является сильно упрощенной и не может достаточно точно описывать д