УСТОЙЧИВОСТЬ ЭЛЕМЕНТОВ КОНСТРУКЦИИ.
Соблюдение условий прочности и жесткости еще не гарантирует способности конструкции выполнять предназначенные ей функции. Так система при некотором значении нагрузки может потерять устойчивость своего начального состояния.
При действии на стержень сжимающих нагрузок не всегда его можно рассчитывать по известному условию прочности.
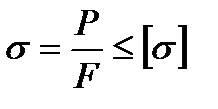
Поскольку при сжатии круглого стержня длиной l >3d уже наблюдается побочное явление, называемое продольным изгибом, при возникновении которого в поперечных сечениях стержня помимо сжимающих нагрузок, начинают действовать изгибающие моменты. Наиболее типичным примером является работа стержня, сжатого силами Р.
При такой нагрузке стержень может сломаться изогнувшись. (пример с линейкой).
Перед изломом сжимающие силы, при которых произойдет разрушение стержня будут значительно ниже тех, которые вызвали бы при простом сжатии напряжение равное пределу прочности материала. Разрушение произойдет потому, что стержень не сможет сохранить форму прямолинейного, а искривится, что вызовет появление изгибающих моментов от сжимающих сил Р и стало быть дополнительных напряжений от изгиба.
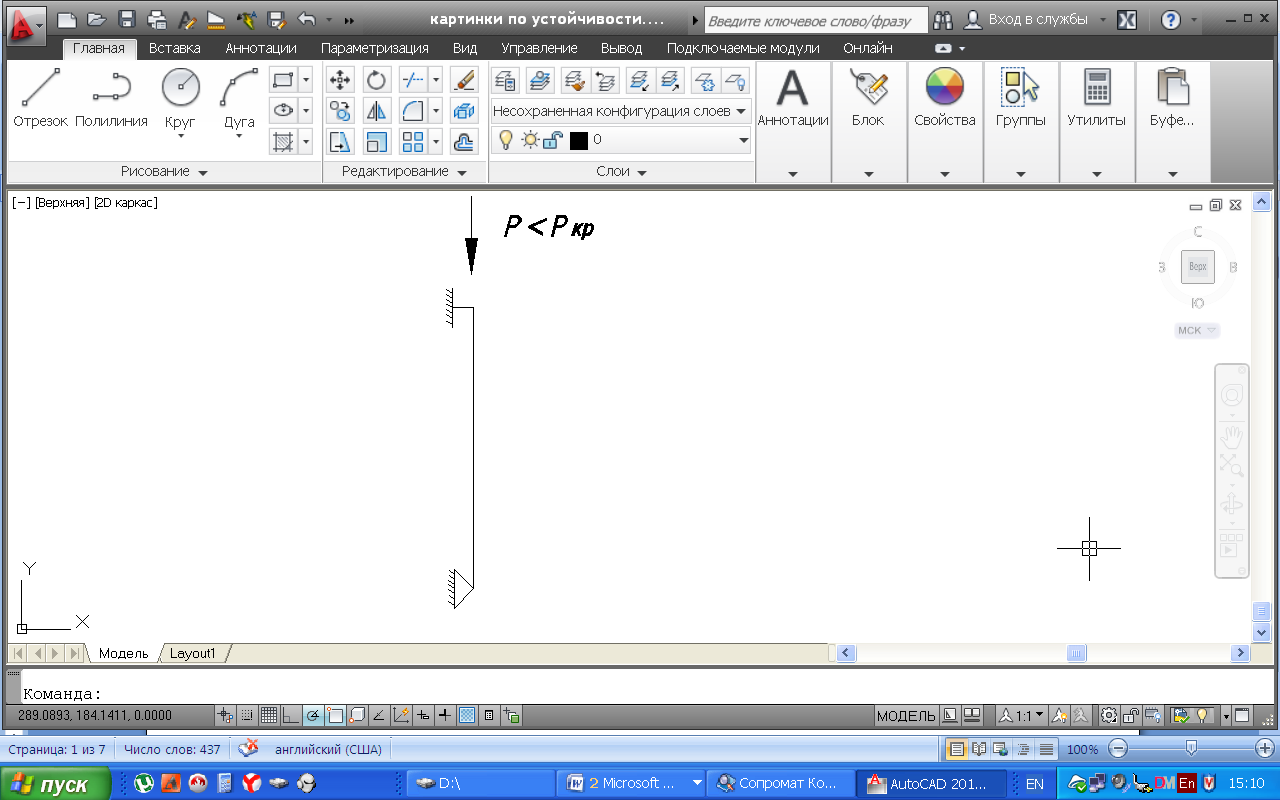 Устойчивость формы равновесия деформированного элемента зависит от величины приложенных нагрузок. Если силы, сжимающие стержень невелики, то первоначальная форма равновесия остается устойчивой (рис.8.1).
Устойчивость формы равновесия деформированного элемента зависит от величины приложенных нагрузок. Если силы, сжимающие стержень невелики, то первоначальная форма равновесия остается устойчивой (рис.8.1).
Рис.20.1. Устойчивая форма равновесия.
Равновесие называется устойчивым, если деформированный элемент при любом малом отклонении от состояния равновесия стремится возвратиться к первоначальному состоянию.
При возрастании нагрузки достигается состояние безразличного равновесия. В этот момент элемент может сохранить первоначально приданную форму, но может и потерять ее от самого незначительного воздействия.
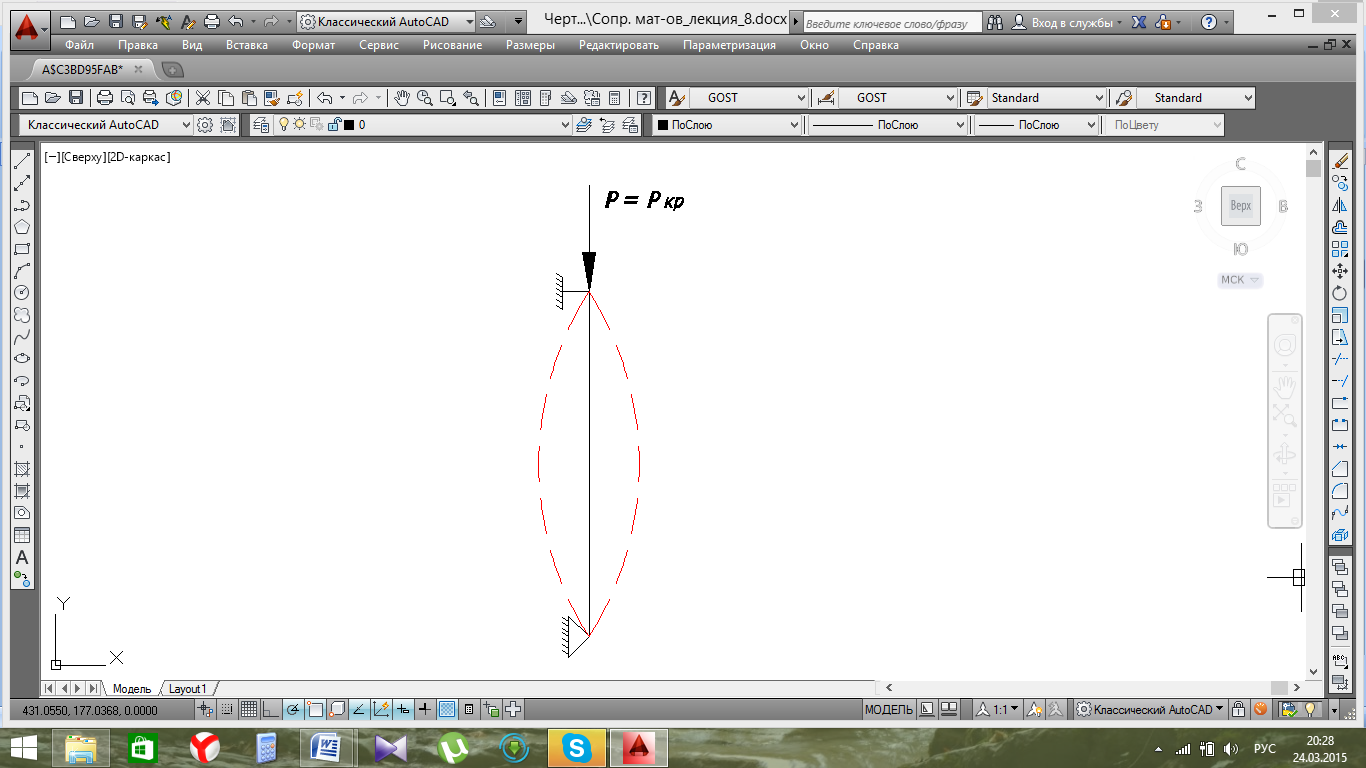
Рис.20.2. Форма безразличного равновесия.
При дальнейшем самом незначительном увеличении нагрузки характер деформации стержня резко меняется – стержень выпучивается, прямолинейная форма равновесия перестает быть устойчивой.
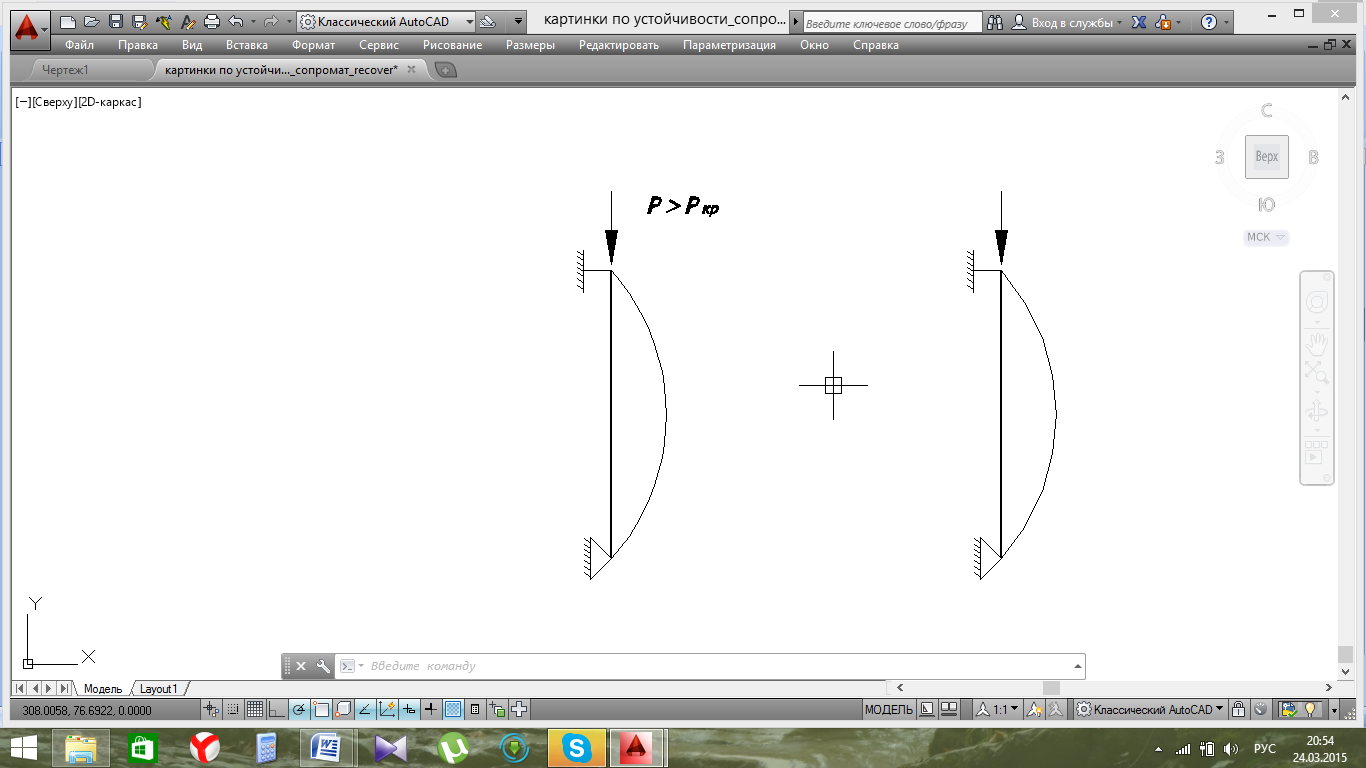
Рис.20.3. Форма неустойчивого равновесия.
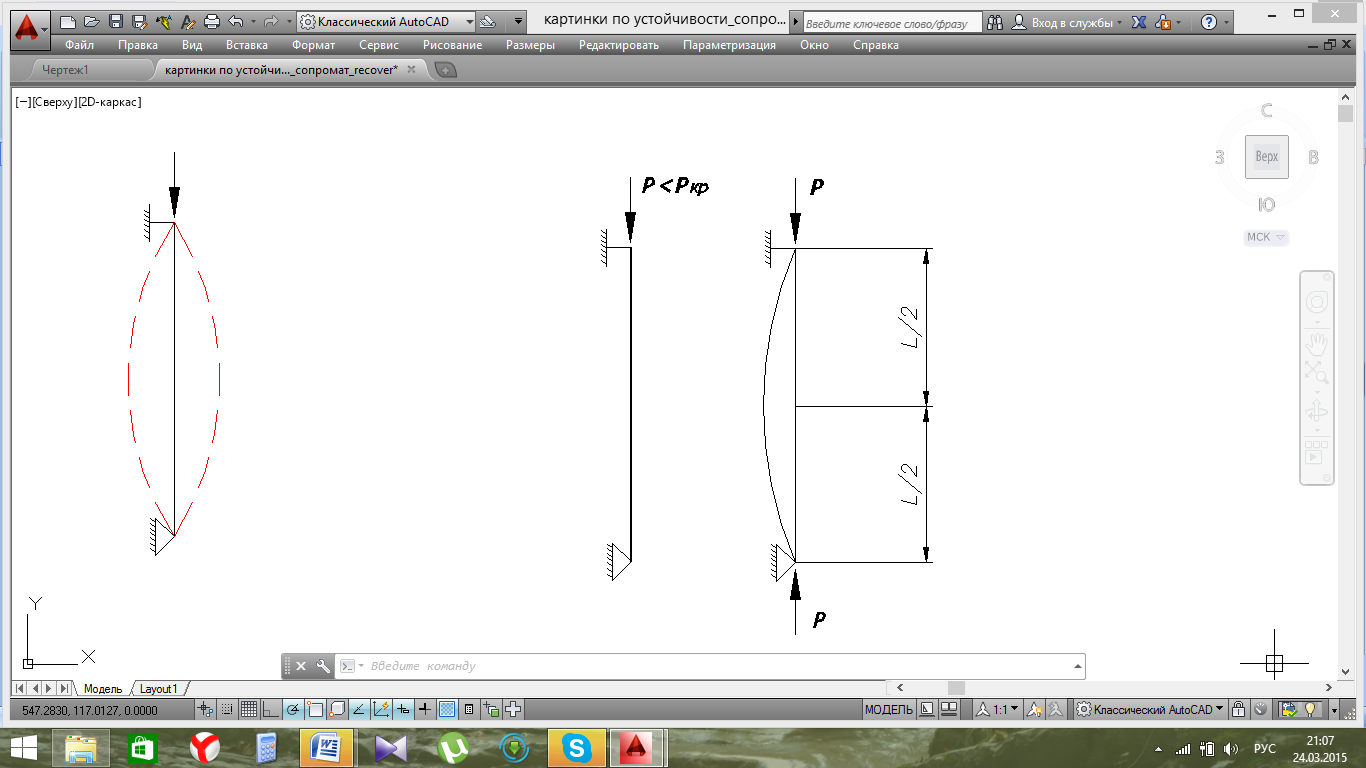 Равновесие называется неустойчивым, если деформированный элемент приобретает стремление продолжать деформироваться в направлении данного ему отклонения.
Равновесие называется неустойчивым, если деформированный элемент приобретает стремление продолжать деформироваться в направлении данного ему отклонения.
Продольный изгиб опасен тем, что при нем происходит очень сильное нарастание прогибов при незначительном росте сжимающей силы. Прогибы и нагрузки связаны между собой нелинейной зависимостью, поэтому быстрое нарастание прогибов вызывает быстрое нарастание напряжений от изгиба и, как следствие, разрушение стержня.
Продольную силу, соответствующую началу появления продольного изгиба принято называть критической силой.
Критическая сила считается опасной или разрушающей, т.к. малейшее превышение ведет к резкому отклонению стержня от первоначального положения и, следовательно, к разрушению, если стержень изготовлен из хрупкого материала или к потери устойчивости системы, если материал пластичен.
Поэтому при расчете стержней на продольный изгиб вводится понятие допустимой силы, которая равна отношению критической силы к коэффициенту устойчивости
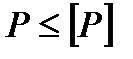
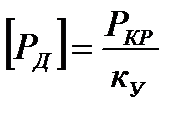
ку - коэффициент устойчивости для каждого материала имеет свои значения. Для стальных 1,8-3 , для чугунных 5-6…
Исследования устойчивости стержневых упругих систем были начаты Леонардо Эйлером.
Эйлер Леонард 1707-1783 – академик Петербургской академии наук.
Для случая потери устойчивости при сжатии или так называемого продольного изгиба, прямого упругого стержня постоянного поперечного сечения шарнирно закрепленного с двух сторон им была выведена формула для критической силы.
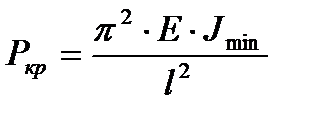
Изогнутая ось нагруженного стержня представляет полуволну синусоиды.
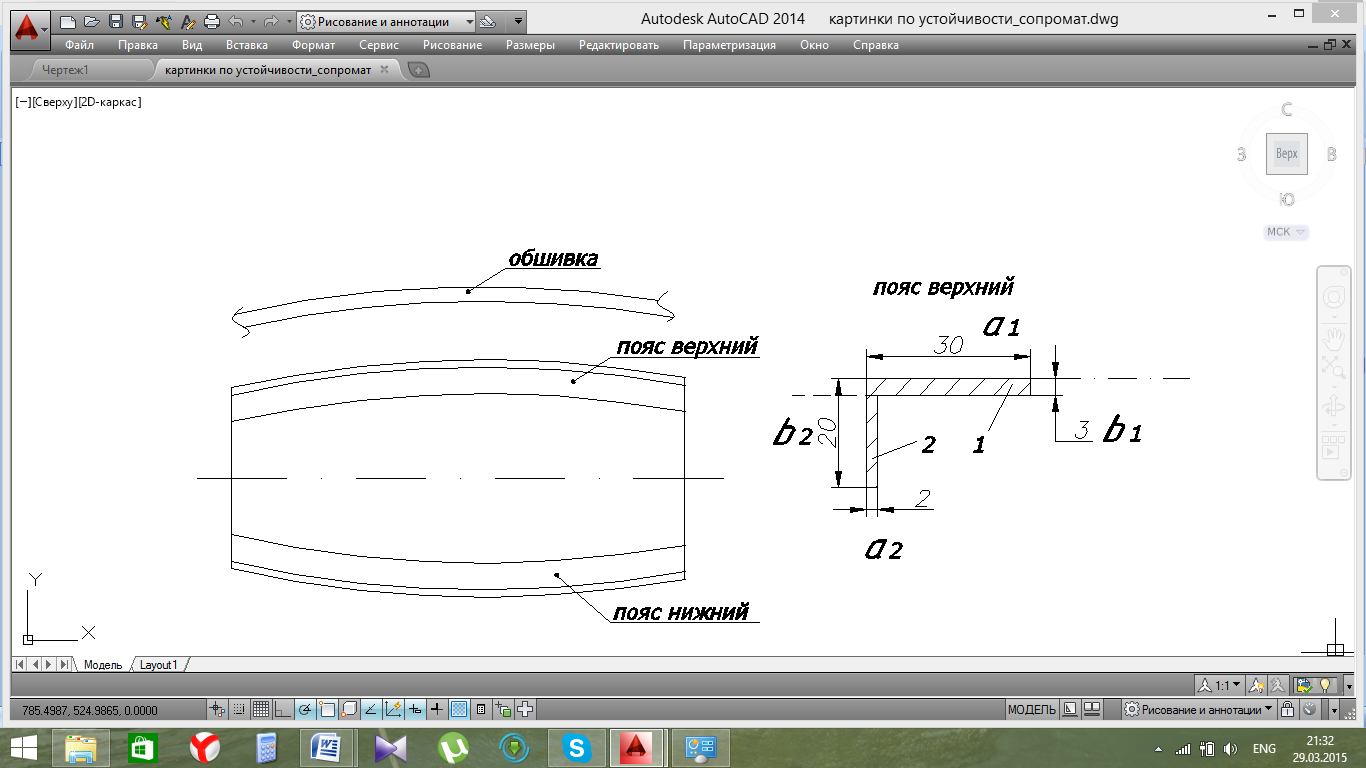
Задача. Проверить на устойчивость и прочность пояс нервюры.
Сечение пояса – уголок 20х2, 30х3; длина пояса 300мм,
Пояс выполнен из профиля материал Д16чТ,
модуль упругости равен Е = 720000кг/см2, предел прочности [σ] =4200кг/см2.
Действующая нагрузка Рсж=2000кг.
Порядок расчета:
1.Определение действующих напряжений;
2.Определение критической силы;
3. Определение критических напряжений;
4.Определение избытков прочности.
1) Определение действующих напряжений 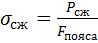
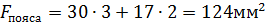
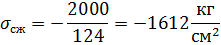
2) Определение критической силы 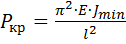
нарисовать горизонтальную ось
у – координата центра тяжести элемента относительно оси Х.
| а (горизонт) | bвертикальный | F,мм2 | у | F∙y | F∙y2 | ic | y0 |
| a1= 30 | b1= 3 | 1,5 | 202,5 | 67,5 | 4,24 | ||
| a2= 2 | b2= 17 | 17/2+3=11,5 | 4496,5 | 818,8 | |||
| S=124 | S=526 | S=4699 | S=886,3 |
iС - собственный момент инерции 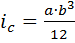
y0 - координата центра тяжести сечения.
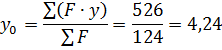
JX – момент инерции относительно оси Х.
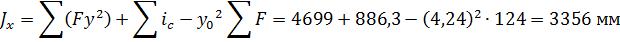
переводим в см, затем считаем Jy аналогично.
| а (горизонт) | bвертикальный | F,мм2 | у | F∙y | F∙y2 | ic | y0 |
| a1= | b1= | ||||||
| a2= | b2= | ||||||
| S= | S= | S= | S= |
Из двух J выбираем наименьшее.
3) Определение критических напряжений
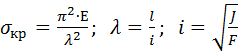
4) Определение избытков прочности.
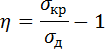
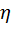 - запас прочности.
- запас прочности.
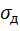 - действующее напряжение.
- действующее напряжение.
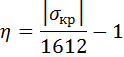
ВЛИЯНИЕ УСЛОВИЙ ЗАКРЕПЛЕНИЯ КОНЦОВ СТЕРЖНЯ НА ВЕЛИЧИНУ КРИТИЧЕСКОЙ СИЛЫ.
Кроме рассмотренного случая встречаются еще три случая заделки краев стержня, работающего на продольный изгиб.
1.Рассмотрим стержень, длиной l , который заделан одним концом и сжат продольной силой, приложенной к свободному концу.
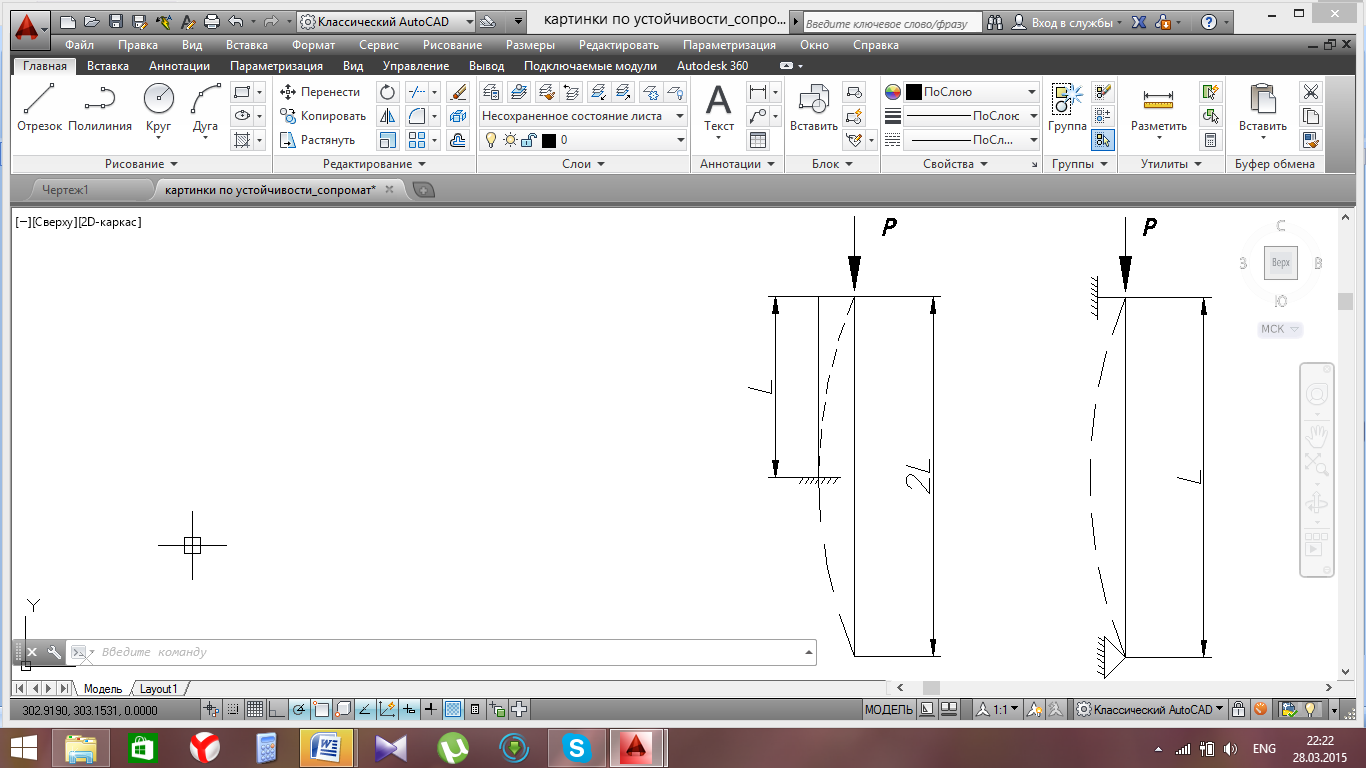
Сравнивая прогиб при шарнирном закреплении с нашим случаем видно, что изогнутая ось стержня, в нашем случае находится в таких же условиях, как и верхняя половина стержня длиной 2l с шарнирно закрепленными концами.
Таким образом, упругая линия будет представлять полуволну синусоиды и критическая сила для стержня в рассматриваемом случае такая же, как и для стержня с шарнирно закрепленными концами при длине L=2l, т.е.
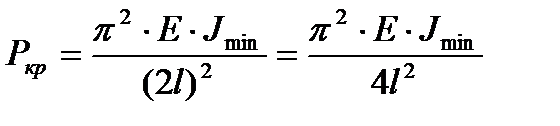
2.Рассмотрим стержень, длиной L , у которого оба конца жестко закреплены.
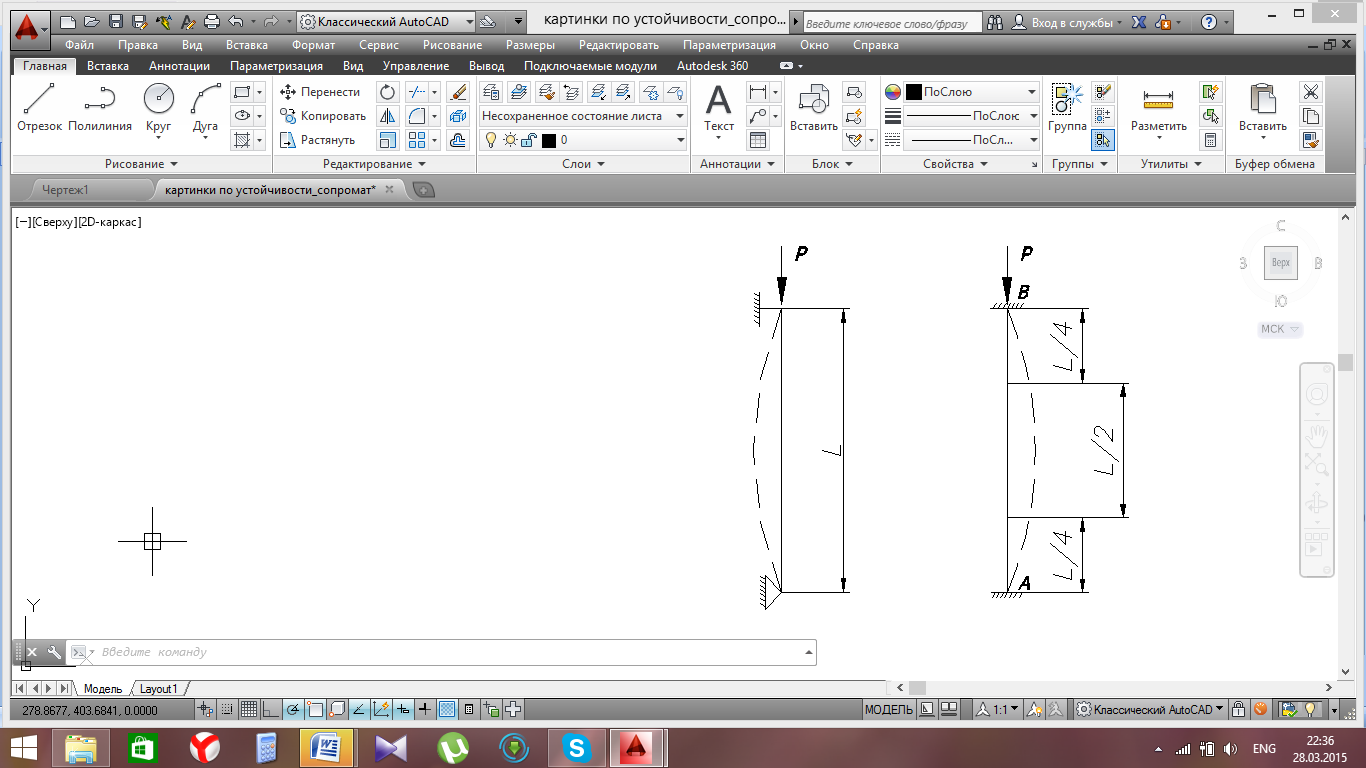
После потери устойчивости стержня вследствие симметрии средняя его часть длиной l/2 работает в тех же условиях, что и стержень при шарнирно опертых концах.
При этом образуются две полуволны: средняя длиной L = l/2 и две крайние половинки полуволны длиной l/4.
Критическую силу в этом случае находим из уравнения при L = l/2
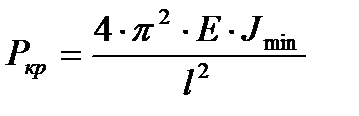
3.Рассмотрим стержень, длиной l , который заделан одним концом и шарнирно оперт на другом.
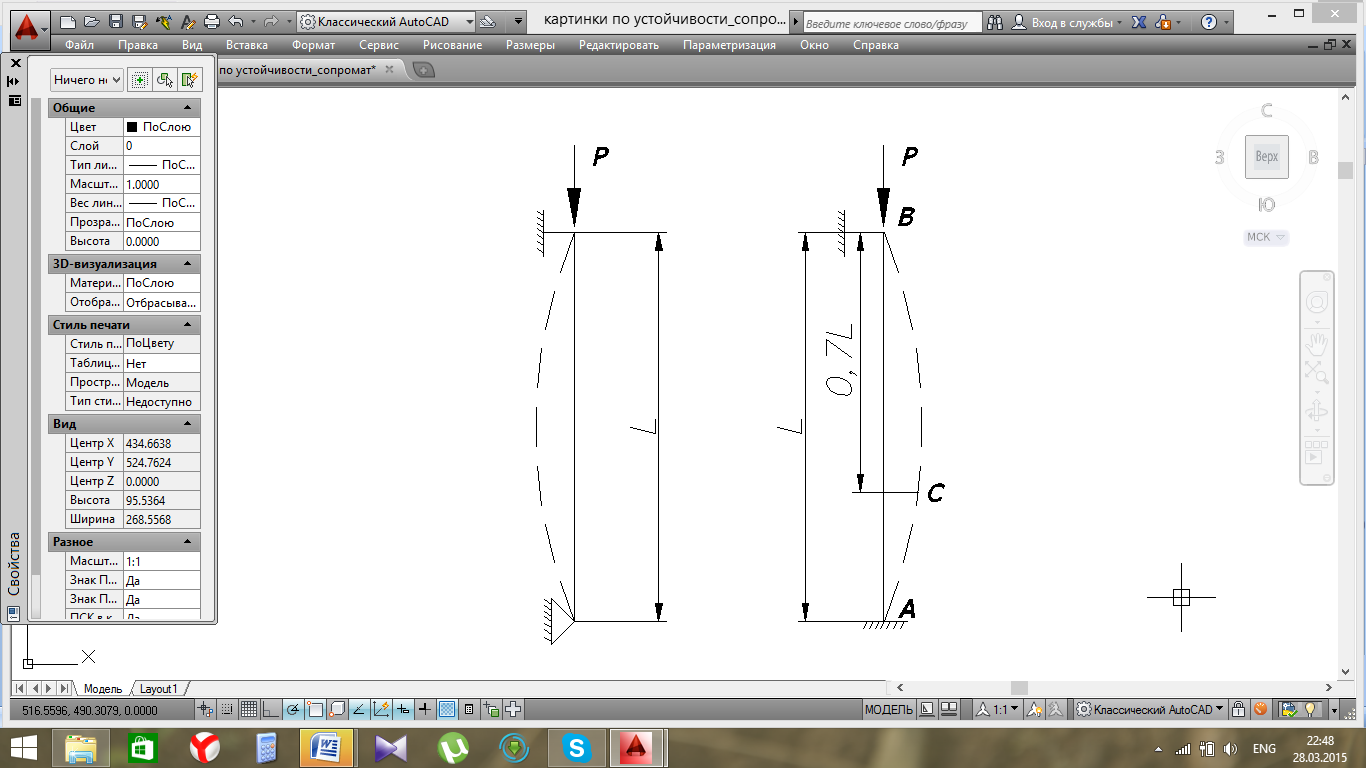
После потери устойчивости правая часть стержня CВ имеет вид полуволны синусоиды. Участок СВ длиной L=0,7l находится в таких же условиях, как и стержень с шарнирно закрепленными концами.
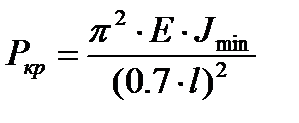
Все вышеуказанные формулы можно объединить в одну:
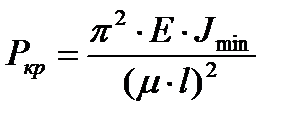
где: 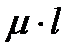 - приведенная длина стержня
- приведенная длина стержня
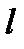 - фактическая длина стержня
- фактическая длина стержня
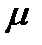 - коэффициент приведения длины.
- коэффициент приведения длины.
Критическое напряжение определяется по формуле:
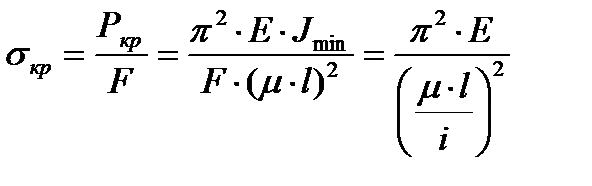
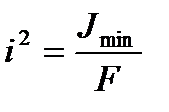 квадрат радиуса инерции
квадрат радиуса инерции
Введем безразмерную величину: 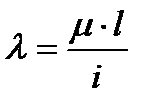 , называемую гибкостью стержня,
, называемую гибкостью стержня,
получим: μ – коэффициент приведения длины. Изменяется в пределах 0,7 - 2
УСЛОВИЕ ПРИМЕНИМОСТИ ФОРМУЛЫ ЭЙЛЕРА.
Вывод формулы Эйлера основан на применении дифференциального уравнения упругой линии. Поэтому пользоваться этой формулой можно лишь в том случае, если справедлив закон Гука, т.е. когда критическое напряжение не превышает предела пропорциональности.
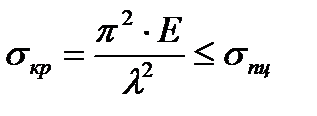
Критическое напряжение стержня зависит только от упругих свойств материала и гибкости стержня.
По мере возрастания гибкости стержня σкр стремится к нулю.
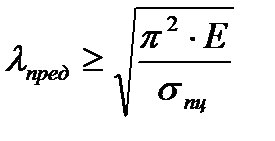
Формула Эйлера непригодна при гибкости стержня меньшей предельного значения гибкости.
Использование формулы для стержней, теряющих устойчивость за пределом упругости дает, завышенные значения критической силы, что может привести к опасным последствиям.
Функциональная зависимость 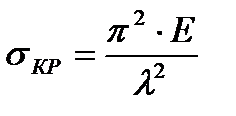
представляет собой видоизменение формулы Эйлера.
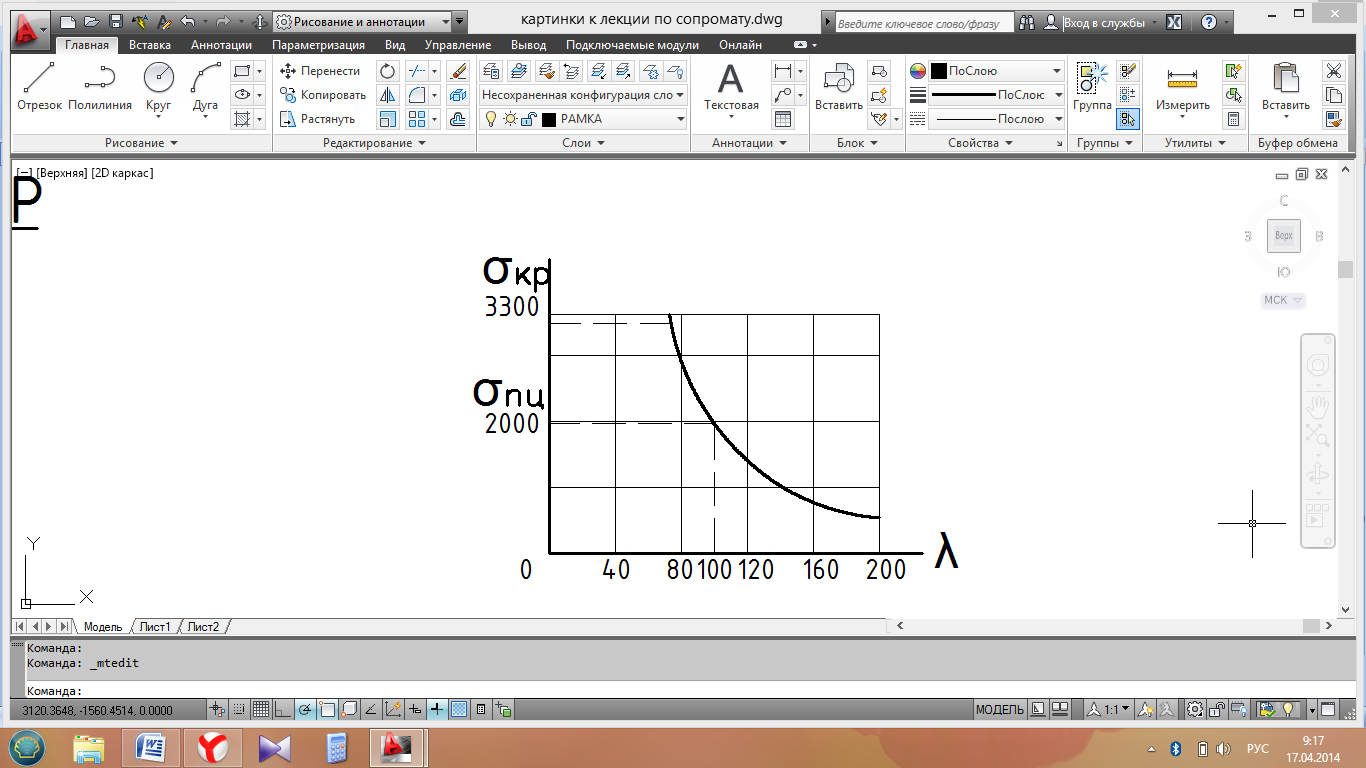 В системе координат σкр – λ эта зависимость может быть представлена гиперболической кривой, называемой гиперболой Эйлера.
В системе координат σкр – λ эта зависимость может быть представлена гиперболической кривой, называемой гиперболой Эйлера.
(материал Ст3)
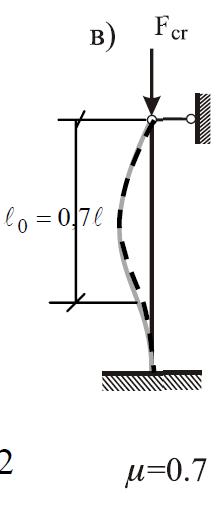 График показывает, что по мере нарастания гибкости стержня критическое напряжение стремится к нулю и наоборот.
График показывает, что по мере нарастания гибкости стержня критическое напряжение стремится к нулю и наоборот.
Если на графике провести горизонтальную линию с ординатой, равной σпц, то она рассечет гиперболу на две части. В верхней части расположены значения напряжений, превышающие σпц, т.е. не соответствующие условиям ее применимости.
Однако явление продольного изгиба продолжает существовать и за пределом упругости. В настоящее время основным источником для установления критических напряжений за пределом пропорциональности являются результаты экспериментов. Теоретическое решение сложно, поэтому обычно пользуются эмпирическими формулами, полученными в результате обработки большого количества опытных данных. Феликс Станиславович Ясинский собрал и обработал обширный опытный материал, в результате чего составил таблицу σкр в зависимости от гибкости для целого ряда материалов и предложил простую эмпирическую формулу для вычисления критических напряжений.
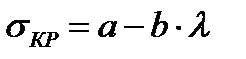
где: а и b - коэффициенты, зависящие от материала;
λ – гибкость стержня.
| <== предыдущая лекция | | | следующая лекция ==> |
| Критерий удельной потенциальной энергии формоизменения | | | УСТАЛОСТЬ МАТЕРИАЛОВ |
Дата добавления: 2017-06-13; просмотров: 4722;










