Кинематика материальной точки

Одним из основных понятий механики является понятие материальной точки, что означает тело, обладающее массой, размерами которого можно пренебречь при рассмотрении его движения. Движение материальной точки – простейшая задача механики, которая позволит рассмотреть более сложные типы движений.

Перемещение материальной точки происходит в пространстве и изменяется со временем. Реальное пространство трехмерно, и положение материальной точки в любой момент времени полностью определяется тремя числами – ее координатами в выбранной системе отсчета. Число независимых величин, задание которых необходимо для однозначного определения положения тела, называется числом его степеней свободы. В качестве системы координат выберем прямоугольную, или декартову, систему координат. Для описания движения точки, кроме системы координат, необходимо еще иметь устройство, с помощью которого можно измерять различные отрезки времени. Выбранная система координат и связанные с ней часы образуют систему отсчета.

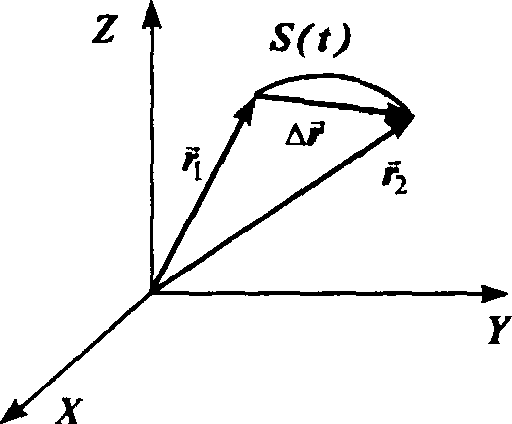Декартовы координаты X,Y,Z определяют в пространстве радиус-вектор z, острие которого описывает при его изменении со временем траекторию материальной точки. Длина траектории точки представляет собой величину пройденного пути S(t). Путь S(t) – скалярная величина. Наряду с величиной пройденного пути, перемещение точки характеризуется направлением, в котором она движется. Разность двух радиус-векторов, взятых в различные моменты времени, образует вектор перемещения точки.

Для того чтобы характеризовать, как быстро меняется положение точки в пространстве, пользуются понятием скорости. Под средней скоростью движения по траектории за конечное время Dt понимают отношение пройденного за это время конечного пути DS ко времени:

.

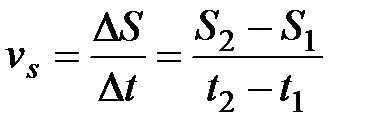Скорость движения точки по траектории – скалярная величина. Наряду с ней можно говорить о средней скорости перемещения точки. Эта скорость – величина, направленная вдоль вектора перемещения,

.

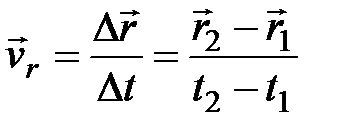Если моменты времени t₁, и t₂бесконечно близки, то время Dt бесконечно мало и в этом случае обозначается через dt. За время dt точка проходит бесконечно малое расстояние dS. Их отношение образует мгновенную скорость точки

.

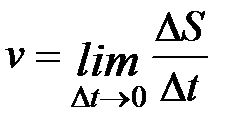Производная радиус-вектора r по времени определяет мгновенную скорость перемещения точки.

.

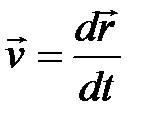Поскольку перемещение совпадает с бесконечно малым элементом траектории dr = dS, то вектор скорости направлен по касательной к траектории, а его величина:

.

На рис. показана зависимость пройденного пути S от времени t. Вектор скорости v(t) направлен по касательной к кривой S(t) в момент времени t. Из рис. видно, что угол наклона касательной к оси t равен

.

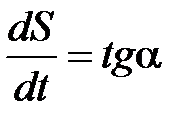Интегрируя выражение в интервале времени от t₀до t, получим формулу, позволяющую вычислить путь, пройденный телом за время t-t₀если известна зависимость от времениего скорости v(t)

.

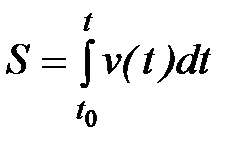Производную скорости по времени, которая является второй производной по времени от радиус-вектора, называют ускорением точки:

.

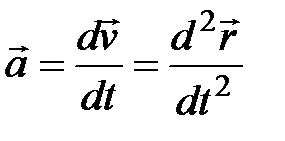Вектор ускорения а направлен вдоль вектора приращения скорости dv. Пусть а = const. Этот важный и часто встречаемый случай носит название равноускоренного или равнозамедленного (в зависимости от знака) движения. Проинтегрируем выражение в пределах от t = 0 до t:

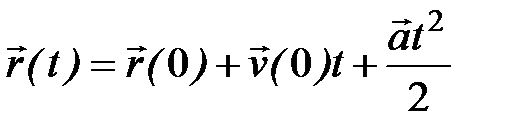
и используем следующие начальные условия: .

Таким образом, при равноускоренном движении

.

В частности, при одномерном движении, например вдоль оси X, 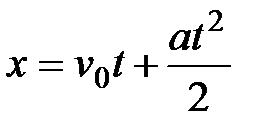. При больших временах зависимость координаты от времени представляет собой параболу.

В общем случае движение точки может быть криволинейным. Рассмотрим этот тип движения. Если траектория точки произвольная кривая, то скорость и ускорение точки при ее движении по этой кривой меняются по величине и направлению.

Выберем произвольную точку на траектории. Как всякий вектор, вектор ускорения можно представить в виде суммы его составляющих по двум взаимно перпендикулярным осям. В качестве одной из осей возьмем направление касательной в рассматриваемой точке траектории, тогда другой осью окажется направление нормали к кривой в этой же точке. Составляющая ускорения, направленная по касательной к траектории, носит название тангенциального ускорения a_t, а направленная ей перпендикулярно – нормального ускорения a_n.

Получим формулы, выражающие величины a_t, и a_n через характеристики движения. Для простоты рассмотрим вместо произвольной криволинейной траектории плоскую кривую. Окончательные формулы остаются справедливыми и в общем случае неплоской траектории. Благодаря ускорению скорость точки приобретает за время dt малое изменение dv. При этом тангенциальное ускорение, направленное по касательной к траектории, зависит только от величины скорости, но не от ее направления. Это изменение величины скорости равно dv. Поэтому тангенциальное ускорение может быть записано как производная по времени от величины скорости:

.

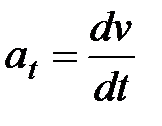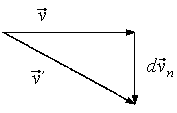
С другой стороны, изменение dv_n, направленное перпендикулярно к v, характеризует только изменение направления вектора скорости, но не его величины.

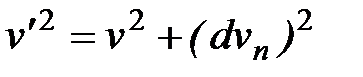, С точностью до величины второго порядка малости величина скорости остается неизменной v=v'.

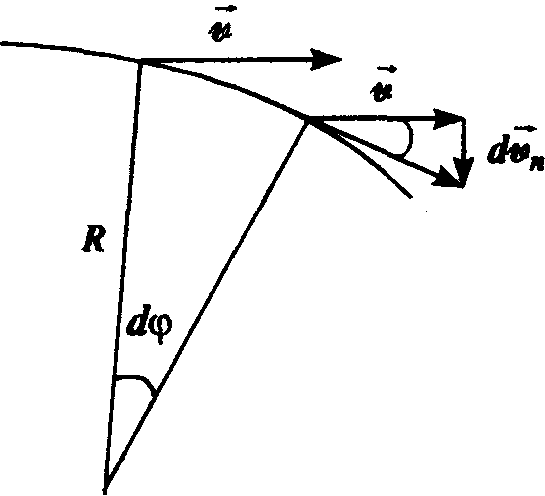Найдем величину a_n. Проще всего это сделать, взяв наиболее простой случай криволинейного движения – равномерное движение по окружности. При этом a_t=0. Рассмотрим перемещение точки за время dt по дуге dS окружности радиуса R.

Скорости v и v' , как отмечалось, остаются равными по величине. Изображенные на рис. треугольники оказываются, таким образом, подобными (как равнобедренные с равными углами при вершинах). Из подобия треугольников следует 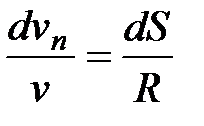, откуда находим выражение для нормального ускорения:

.

Формула для полного ускорения при криволинейном движении имеет вид:

.

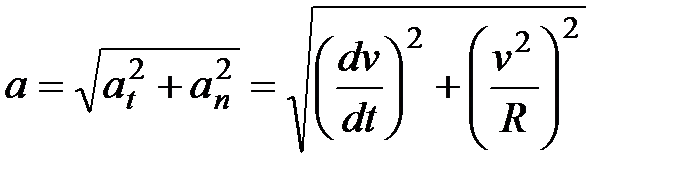Подчеркнем, что эти соотношения справедливы для всякого криволинейного движения, а не только для движения по окружности. Это связано с тем, что всякий участок криволинейной траектории в достаточно малой окрестности точки можно приближенно заменить дугой окружности. Радиус этой окружности, называемый радиусом кривизны траектории, будет меняться от точки к точке и требует специального вычисления. Таким образом, последняя формула остается справедливой и в общем случае пространственной кривой.