Метод Эйлера (метод ломаных)
Рассмотрим уравнение (7.1) в точках xi, i = 0, 1, …, n – 1 и заменим производную  разностной формулой
разностной формулой
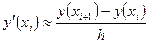 . (7.4)
. (7.4)
Тогда получим рекуррентную формулу метода Эйлера для вычисления приближенных значений y(xi + 1):
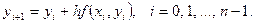 (7.5)
(7.5)
Здесь через yi обозначены приближенные значения y(xi), т.е. yi ≈ y(xi),
i = 1, 2, …, n.
На рис. 7.1 дана геометрическая иллюстрация метода Эйлера (7.5). Уравнение касательной к графику решения y(x) в точке (x0, y0) имеет вид
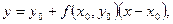 (7.6)
(7.6)
так как  . Интегральная кривая y(x) на отрезке [x0, x1] заменяется отрезком касательной (7.6), соединяющей точку (x0, y0) с точкой (x1, y1), где
. Интегральная кривая y(x) на отрезке [x0, x1] заменяется отрезком касательной (7.6), соединяющей точку (x0, y0) с точкой (x1, y1), где  (см. рис. 7.1). Точка (x1, y1) уже не лежит на интегральной кривой y = y(x), удовлетворяющей начальному условию (7.2).
(см. рис. 7.1). Точка (x1, y1) уже не лежит на интегральной кривой y = y(x), удовлетворяющей начальному условию (7.2).
При i = 1 формула (7.5) дает точку (x2, y2), которая определяется с помощью касательной  проведенной в точке (x1, y1) к интегральной кривой y(x), удовлетворяющей уравнению (7.1) и начальному условию
проведенной в точке (x1, y1) к интегральной кривой y(x), удовлетворяющей уравнению (7.1) и начальному условию  .
.
Таким образом, с каждым шагом i метод Эйлера (7.5) дает точки (xi, yi), которые, вообще говоря, удаляются от интегральной кривой, соответствующей точному решению задачи Коши (7.1), (7.2). Вместо интегральной кривой метод Эйлера дает ломаную, изображенную на рис. 7.1, поэтому его часто называют методом ломаных.

Рис.7.1.
Формулу (7.5) можно получить и другим способом. Рассмотрим разложение искомого решения y(x) в ряд Тейлора в окрестности точки x0:
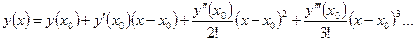
Ограничившись двумя слагаемыми и учитывая, что 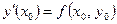 , при x = x1 получим (7.5).
, при x = x1 получим (7.5).
Мы также получили следующий результат — погрешность вычисления значения y1 есть величина порядка O(h2), а погрешность значения yn — величина порядка O(h). Из-за большой погрешности метод Эйлера применяется редко.
Пример 7.1. Решить методом Эйлера на отрезке [1, 2] задачу Коши

Решение в программе Excel. Точным решением данной задачи является функция 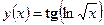 .
.
Выберем шаг h = 0,1.
В диапазоне A1:B12 заполняем ячейки, как показано в таблице 7.1.
В ячейке D2 записываем начальное значение y(0) = 1, а в ячейке C2 — формулу =(1+C2^2)*0,5/A2, которая соответствует выражению f(x0, y0). Затем выделим ячейку C2 и маркером заполнения протянем вниз до C11.
В ячейку D3 введем формулу =D2+0,1*C2 и протянем ячейку D3 маркером заполнения вниз до D12.
В столбце E2:E12 вычислим значения точного решения. Для этого в ячейку E2 введем формулу =TAN(LN(КОРЕНЬ(A2))) и протянем ячейку E2 маркером заполнения вниз до E12.
В столбце F2:F12 вычислим абсолютные ошибки с помощью формулы =ABS(C2-D2), введенной в ячейку F2 и скопированной в остальные ячейки.
Как видим, значения, полученные методом Эйлера, приближенно равны точным значениям. Абсолютная погрешность каждого значения равна в среднем ε ≈ 0,01. При этом видно, что погрешность yi+1 увеличивается вместе с номером i.
Таблица 7.1
| A | B | C | D | E | F | |
| i | xi | f(xi,yi) | yi | y(x) | Ошибки | |
| 0,5 | ||||||
| 1,1 | 0,455682 | 0,05 | 0,047691 | 0,002309 | ||
| 1,2 | 0,420472 | 0,095568 | 0,091414 | 0,004154 | ||
| 1,3 | 0,391899 | 0,137615 | 0,13194 | 0,005676 | ||
| 1,4 | 0,368307 | 0,176805 | 0,169842 | 0,006964 | ||
| 1,5 | 0,348547 | 0,213636 | 0,205556 | 0,00808 | ||
| 1,6 | 0,331796 | 0,248491 | 0,239426 | 0,009065 | ||
| 1,7 | 0,317452 | 0,28167 | 0,27172 | 0,00995 | ||
| 1,8 | 0,305064 | 0,313416 | 0,302658 | 0,010758 | ||
| 1,9 | 0,294285 | 0,343922 | 0,332418 | 0,011503 | ||
| 0,37335 | 0,36115 | 0,0122 |
Создадим в программе Excel пользовательские функции для решения задачи Коши (7.1), (7.2) методом Эйлера, используя встроенный язык Visual Basic. Правую часть уравнения (7.1) для нашего примера определяет функция fxy(x, y):
Function fxy(ByVal x, ByVal y): fxy = (1 + y ^ 2) / (2 * x): End Function
Метод Эйлера реализует функция Eiler(x0, y0, x, n):
Function Eiler(ByVal x0, ByVal y0, ByVal x, ByVal n)
h = (x - x0) / n
For i = 1 To n
y1 = y0 + h * fxy(x0, y0): x0 = x0 + h: y0 = y1
Next i: Eiler = y1: End Function
Ключевое слово ByVal в списке параметров указывает на то, что каждый параметр будет передаваться по значению.
Здесь исходными данными являются начальные значения x0, y0, значение переменной x и числовой параметр n, который означает число частей, на которые разбивается отрезок [x0, x], т.е. метод Эйлера применяется с шагом h = (x - x0) / n. Результатом является приближенное значение решения в точке x.
Чтобы ввести эти функции в Excel, выполним команду «Сервис – макрос – Редактор Visual Basic» и в открывшемся окне выбираем пункт меню «Insert – Module» и вводим тексты программ-функций (см. рис. 7.2). Теперь эти функции можно использовать в формулах, как и обычные функции программы Excel.
Переходим в Excel, и построим таблицу решения примера 7.1 с помощью созданных функций. В таблице 7.2 приведены результаты вычислений, а в таблице 7.3 показаны формулы. Уменьшение погрешности по сравнению с таблицей 7.1 объясняется тем, что метод Эйлера в таблице 7.2 применяется с шагом h = 0,01.
Отметим, что правая часть уравнения вызывается в описании функции Eiler. Если понадобится решить задачу Коши с другой правой частью, то достаточно переопределить функцию fxy(x, y).
Таблица 7.2
| A | B | C | D | |
| xi | yi | y(x) | Ошибки | |
| 1,1 | 0,047914 | 0,047691 | 0,000223 | |
| 1,2 | 0,091817 | 0,091414 | 0,000403 | |
| 1,3 | 0,132492 | 0,13194 | 0,000552 | |
| 1,4 | 0,17052 | 0,169842 | 0,000678 | |
| 1,5 | 0,206345 | 0,205556 | 0,000788 | |
| 1,6 | 0,240311 | 0,239426 | 0,000885 | |
| 1,7 | 0,272693 | 0,27172 | 0,000973 | |
| 1,8 | 0,30371 | 0,302658 | 0,001052 | |
| 1,9 | 0,333545 | 0,332418 | 0,001126 | |
| 0,362345 | 0,36115 | 0,001195 |
Таблица 7.3
| A | B | C | D | |
| xi | yi | y(x) | Ошибки | |
| =TAN(LN(КОРЕНЬ(A2))) | =ABS(B2-C2) | |||
| 1,1 | =Eiler(A2;B2;A3;10) | =TAN(LN(КОРЕНЬ(A3))) | = ABS (B3-C3) | |
| 1,2 | =Eiler(A3;B3;A4;10) | =TAN(LN(КОРЕНЬ(A4))) | = ABS (B4-C4) | |
| 1,3 | =Eiler(A4;B4;A5;10) | =TAN(LN(КОРЕНЬ(A5))) | = ABS (B5-C5) | |
| 1,4 | =Eiler(A5;B5;A6;10) | =TAN(LN(КОРЕНЬ(A6))) | = ABS (B6-C6) | |
| 1,5 | =Eiler(A6;B6;A7;10) | =TAN(LN(КОРЕНЬ(A7))) | = ABS (B7-C7) | |
| 1,6 | =Eiler(A7;B7;A8;10) | =TAN(LN(КОРЕНЬ(A8))) | = ABS (B8-C8) | |
| 1,7 | =Eiler(A8;B8;A9;10) | =TAN(LN(КОРЕНЬ(A9))) | = ABS (B9-C9) | |
| 1,8 | =Eiler(A9;B9;A10;10) | =TAN(LN(КОРЕНЬ(A10))) | = ABS (B10-C10) | |
| 1,9 | =Eiler(A10;B10;A11;10) | =TAN(LN(КОРЕНЬ(A11))) | = ABS (B11-C11) | |
| =Eiler(A11;B11;A12;10) | =TAN(LN(КОРЕНЬ(A12))) | = ABS (B12-C12) |
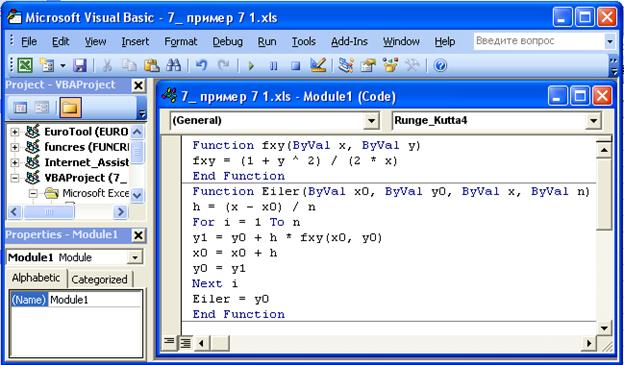
Рис.7.2. Окно редактора Visual Basic
Создадим в программе Mathcad функции для решения задачи Коши методом Эйлера и вычислим решение в точке x = 2 с шагом h = 0,1 (n = 10) и шагом h = 0,01 (n = 100):
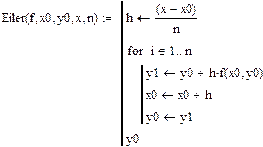
|

|
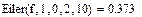
|

|
Как видим, результаты расчетов в программе Mathcad совпадают со значениями, полученными в Excel.
Дата добавления: 2021-09-07; просмотров: 344;










