Dummy – переменные, фиктивные переменные
Как правило, независимые переменные в регрессионных моделях имеют непрерывные области распределения. Однако некоторые переменные могут иметь всего два или дискретное множество значений, например: пол, уровень образования, рейтинг, оценка и т.д.
Например: рассмотрим в качестве зависимой переменной  – заработная плата, а
– заработная плата, а 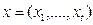 - набор объясняющих переменных.
- набор объясняющих переменных.
Хотим в модель включить новую бинарную переменную, отвечающую за наличие или отсутствие высшего образования. Тогда необходимо включить в модель новую переменную d (d=1, если t-ый рабочий имеет высшее образование; d=0, если не имеет)
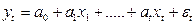
и рассмотреть новую модель
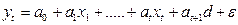
Тогда средняя заработная плата для людей без высшего образования =  ; с высшим образованием =
; с высшим образованием = 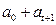
Т.е. коэффициент  интерпретируется как среднее изменение з/п при переходе из одной категории в другую при неизменных остальных параметрах. Т.е. люди с высшим образованием получают на
интерпретируется как среднее изменение з/п при переходе из одной категории в другую при неизменных остальных параметрах. Т.е. люди с высшим образованием получают на  рублей больше. Если коэффициент перед
рублей больше. Если коэффициент перед  незначим, т.е. его р>0,05, то различий в з/п между категориями нет.
незначим, т.е. его р>0,05, то различий в з/п между категориями нет.
Замечание: качественное различие можно формализовать с помощью любой переменной, принимающей два значения, а не обязательно 0 и1. Но тогда интегрируемость коэффициента  усложняется.
усложняется.
Замечание: если включающаяся в модель dummy переменная имеет не два, а несколько значений, то в принципе можно было бы ввести дискретную переменную, принимающую такое же количество значений, но тогда, во-первых, затрудняется интерпретация, во-вторых, подразумевается одинаковое различие между состояниями признака. Поэтому вводят несколько бинарных переменных.
Пример: пусть оценивается стоимость мобильного телефона. В качестве дискретного признака выступает вид телефона:
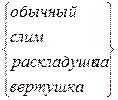
Вводятся 4 бинарных переменных
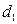
 , если телефон обычный;
, если телефон обычный; 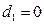 , в остальных случаях
, в остальных случаях
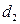
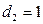 , если телефон слим;
, если телефон слим; 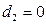 , в остальных случаях
, в остальных случаях
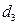
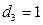 , если телефон раскладушка;
, если телефон раскладушка; 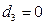 , в остальных случаях
, в остальных случаях
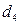
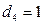 , если телефон вертушка;
, если телефон вертушка; 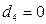 , в остальных случаях
, в остальных случаях
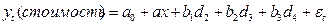
Мы не включили в модель 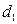 , т.к. тогда для любой строки выполнялось бы
, т.к. тогда для любой строки выполнялось бы 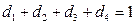 , т.е. регрессоры были бы линейно зависимы, т.е. мы не смогли бы получить МНК-оценку параметров, т.к. не смогли бы обратить матрицу.
, т.е. регрессоры были бы линейно зависимы, т.е. мы не смогли бы получить МНК-оценку параметров, т.к. не смогли бы обратить матрицу.
Интерпретация коэффициентов:
Средняя стоимость телефона слим: 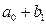 , раскладушка:
, раскладушка: 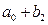 , вертушка:
, вертушка: 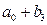
Замечание: если рассматривается ситуация, когда бинарная переменная описывает не все возможные варианты, то в модель включаются все переменные.
Пример: если рассматривается вторичный рынок квартир в Москве, то зависимая переменная – это стоимость 1 кв.м. В качестве одного из факторов используют количество комнат и включают в модель 4 новые переменные следующего вида:
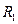
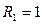 , если одна комната;
, если одна комната;  , если нет
, если нет
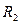
 , если две комнаты;
, если две комнаты; 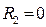 , если нет
, если нет
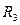
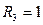 , если три комнаты;
, если три комнаты; 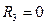 , если нет
, если нет
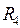
 , если четыре комнаты;
, если четыре комнаты;  , если нет
, если нет
В модель включаются все 4 переменные, т.к. в базе данных по квартирам присутствуют и многокомнатные квартиры, т.е. больше четырех комнат.
Прогнозирование
После построения регрессионного уравнения и оценки значимости ее коэффициентов, можно получить предсказанное значение результата 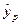 с помощью точного прогноза при заданном значении фактора
с помощью точного прогноза при заданном значении фактора 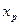 . Для этого в полученное уравнение регрессии
. Для этого в полученное уравнение регрессии  надо подставить факторы
надо подставить факторы 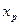 , после чего получить прогноз. Это так называемый точечный прогноз, но он не дает требуемых представлений, и мало применим на практике. Поэтому дополнительно необходимо осуществить определение стандартной ошибки прогнозирования
, после чего получить прогноз. Это так называемый точечный прогноз, но он не дает требуемых представлений, и мало применим на практике. Поэтому дополнительно необходимо осуществить определение стандартной ошибки прогнозирования 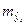 и получить интервальную оценку прогнозного значения.
и получить интервальную оценку прогнозного значения.
Чтобы построить интервальный прогноз, необходимо найти верхнюю и нижнюю границы. Найдем сначала формулу стандартной ошибки прогнозирования 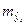 . Вставим в формулу линейной регрессии значение параметра . Тогда уравнение регрессии имеет следующий вид:
. Вставим в формулу линейной регрессии значение параметра . Тогда уравнение регрессии имеет следующий вид:
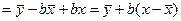
Из этой формулы следует, что стандартная ошибка прогнозирования зависит от ошибки y-среднее и ошибки коэффициента регрессии b. Тогда
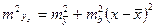
 , если
, если 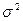 - неизвестна, то ее заменяют на оценку дисперсии
- неизвестна, то ее заменяют на оценку дисперсии 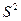
Учитывая ошибку регрессии 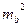 ,получаем следующую формулу для прогноза:
,получаем следующую формулу для прогноза:

Тогда интервальный прогноз или доверительный интервал прогнозируемого значения рассчитывается следующим образом:
 , где
, где 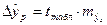 -предельная ошибка прогноза
-предельная ошибка прогноза
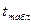 - кванти с уровнем доверия
- кванти с уровнем доверия 
Например:  =0,95, то истинное значение попадет в доверительный интервал
=0,95, то истинное значение попадет в доверительный интервал  с вероятностью 0,95
с вероятностью 0,95
Строя прогноз, мы хотим получить как можно более точный прогноз и как можно меньший интервал (узкий), но чем выше  , тем дальше друг от друга границы интервала и наоборот. Поэтому приходится искать компромисс. Часто в задачах
, тем дальше друг от друга границы интервала и наоборот. Поэтому приходится искать компромисс. Часто в задачах  задано заказчиками исследования. Поэтому, строя модель, мы должны помнить, что хорошая модель – это та, интервальные прогнозы, по которой достаточно точные и границы не слишком далеко друг от друга, а сам интервал неширокий.
задано заказчиками исследования. Поэтому, строя модель, мы должны помнить, что хорошая модель – это та, интервальные прогнозы, по которой достаточно точные и границы не слишком далеко друг от друга, а сам интервал неширокий.
Замечание: если построенная по выборке модель имеет высокий 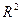 , все оценки значимы, остатки близки к нормальным, но прогнозы неточные, широкие интервалы прогнозирования (плохая прогностическая способность модели), то, возможно, вы просто подогнали модель под данные и она не подходит, т.е. ее надо переделать, т.е. прогнозирование можно использовать в качестве оценки качества модели.
, все оценки значимы, остатки близки к нормальным, но прогнозы неточные, широкие интервалы прогнозирования (плохая прогностическая способность модели), то, возможно, вы просто подогнали модель под данные и она не подходит, т.е. ее надо переделать, т.е. прогнозирование можно использовать в качестве оценки качества модели.
Дата добавления: 2022-05-27; просмотров: 140;











