Эллиптический или фильтр Кауэра
Это фильтры объединяют в себе свойства фильтров Чебышева первого и второго рода, поскольку АЧХ такого фильтра имеет пульсации, заданного уровня, как в полосе пропускания, так и в полосе задерживания, что позволяет получить высокую крутизну скатов АЧХ.
Функция передачи имеет как полюсы, так и нули. Нули, как и в случае Чебышева второго рода, являются чисто мнимыми и образуют комплексно-сопряженные пары. Количество нулей функции равно максимальному четному числу, но не превосходит порядок фильтра.
Для определения числа звеньев в фильтре необходимо определить ряд вспомогательных параметров: ε, k, k1, k', k1'.
Здесь ε – параметр определяющий пульсацию в полосе пропускания an = 10lg(1 + ε2); k и k1 – модули полных эллиптических интегралов, которые изменяются в пределах от 0 до 1, а k' и k1' – дополнительные модули от k и k1 соответственно. Они могут быть определены следующим образом:
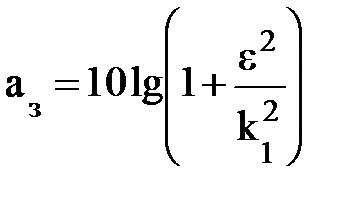 ,
,
отсюда 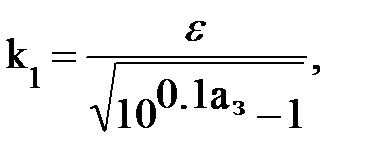
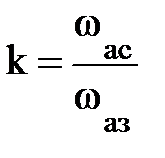 и служит мерой изменения характеристики фильтра в переходной полосе;
и служит мерой изменения характеристики фильтра в переходной полосе; 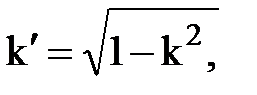 а
а 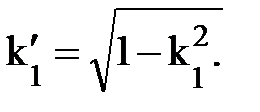
Очевидно, что параметры ε, k и n связаны друг с другом и не могут быть выбраны произвольно. При этом число звеньев эллиптического фильтра находится по следующей формуле:
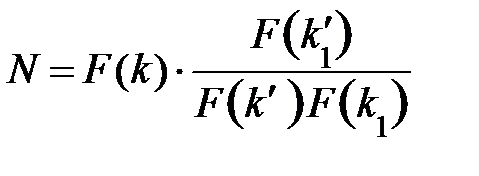
где F(k), F(k1), F(k'), F(k1') – полные эллиптические интегралы с соответствующими модулями.
Нули и полюса функции передачи эллиптического фильтра определяется так [6]:
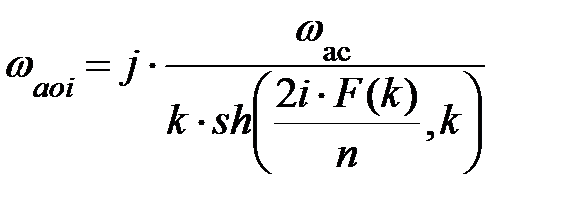 ,
,
для N – нечетного,
здесь sn(u, k) – эллиптический синус Якоби по модулю k;
i = 0, ±1, …, ± 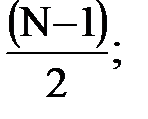
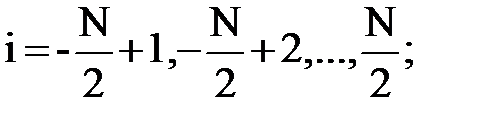
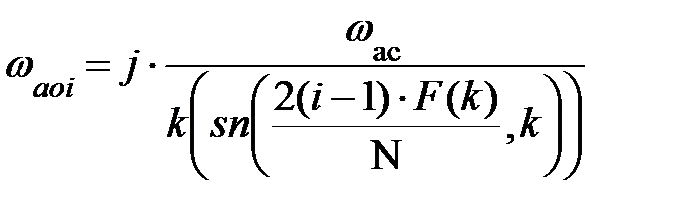 ,
, 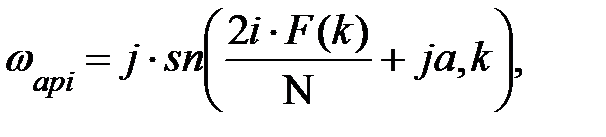
для N – четного, для N – нечетного,
здесь эллиптический синус определяется от комплексного аргумента и параметр 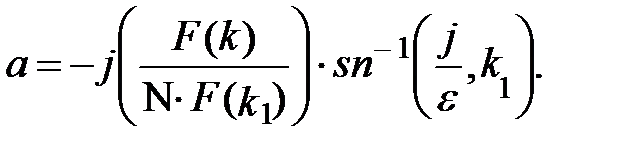
Символ sn-1(u,k) служит для обозначения обратного эллиптического синуса, а i = 0, ±1, ±2, ±…, ± 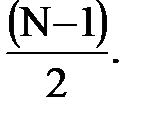
Для N – четного полюса определяются так:
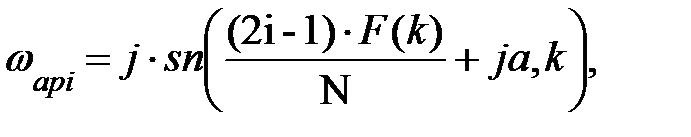 где
где 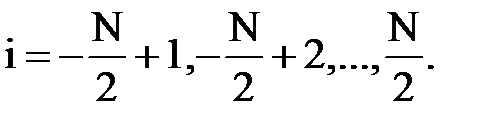
Дата добавления: 2017-05-02; просмотров: 3490;










