Структурные схемы систем и их типовые динамические звенья

При решении задач анализа и синтеза в теории автоматического управления широко используются структурные схемы. Они позволяют исследовать различные по природе и конструкции системы регулирования с помощью единого математического аппарата. Структурные схемы содержат узлы разветвления, узлы суммирования и динамические звенья (рис. 6.11, а, б, в).

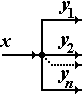
а б в

Рис. 6.11. Элементы структурных схем:

а – узел разветвления; б – узел суммирования, в – динамическое звено.

Узел разветвления. В таком узле (рис. 6.11, а) входной сигнал х разделяется, не меняя своего значения, и направляется далее по нескольким каналам

y₁ = y₂ = … = y_n = х, (6.35)

где y₁, y₂,…, y_n – сигналы в выходных каналах узла разветвления.

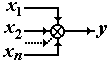
Суммирующий узел (сумматор), к которому подходит несколько (рис. 6.11, б) сигналов х₁, х₂,…, х_n, формирует на выходе только один сигнал y, равный алгебраической сумме входных сигналов

y = х₁ + х₂ + … + х_n. (6.36)

Динамическое звено. Проходя динамическое звено, входной сигнал х изменяет сигнал на выходе y по форме и величине (в некоторых случаях только по величине).

В основу классификации звеньев положены соответствующие уравнения динамики. Переходные процессы систем регулирования (пневматических, электрических, механических и др.), имеющих разную физическую природу и различное конструктивное оформление, но обладающих одинаковыми динамическими свойствами, подобны. Поэтому каждая такая система описывается одним или несколькими одинаковыми звеньями.

Большинство звеньев обладает направленностью действия (детектирующее свойство). Сигнал проходит через них только в одном направлении – с входа звена на его выход, в обратном направлении звено сигнал не пропускает. Например, изменение температуры рабочего спая термоэлектрического преобразователя приводит к изменению термоэлектродвижущей силы на его свободных концах.

Звенья систем могут быть статическими и астатическими. У статического звена при постоянном входном воздействии выходная величина со временем устанавливается на постоянном значении, отличном от первоначального, а у астатического звена в установившемся режиме выходная величина непрерывно изменяется с постоянной скоростью или ускорением.

Динамические звенья называют типовыми, если изменение проходящего через них сигнала описывается алгебраическим или дифференциальным уравнением не выше 2-го порядка. Они имеют одну входную и одну выходную величину. Типовыми звеньями являются: усилительное, интегрирующее, дифференцирующее, апериодическое, колебательное и запаздывающее.

Соединения звеньев. В реальных системах соединения звеньев могут быть весьма причудливыми (в форме магистралей, колец, звезд и т.д.), однако в конечном итоге они могут быть преобразованы к трем видам: последовательному, параллельному, а также в соединения с замкнутой обратной связью (рис. 6.12). При последовательном соединении звеньев (рис. 6.12, а) выходная величина предыдущего звена без искажения поступает на вход последующего звена. При таком соединении звеньев входной величиной является входная величина первого по ходу сигнала звена, а выходной – выходная величина последнего из них.

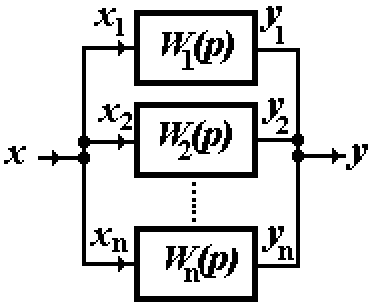
При параллельном соединении звеньев (рис. 6.12, б) входной сигнал через узел разветвления поступает на входы всех элементарных звеньев. Выходные сигналы этих звеньев суммируются и направляются на выход соединения.

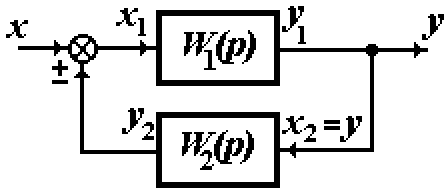
При замкнутой обратной связи (рис. 6.12, в) система образует контур и состоит из двух звеньев, каждое из которых может представлять собой достаточно сложное соединение. По первому звену сигнал проходит от входа соединения к его выходу, т.е. по прямой связи, а по второму – от выхода соединения к входу, т.е. по обратной связи. При этом на вход первой цепочки звеньев подается сигнал х₁, равный сумме входной величины соединения х и выходной величины второй цепочки звеньев y₂:

х₁ = х + y₂. (6.37)

Выходной величиной такого соединения y является выход первого звена; одновременно этот же сигнал подается на вход второго звена. При этом y₂ называется сигналом обратной связи.

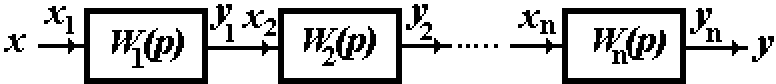
а

б в

Рис. 6.12. Типы соединений звеньев:

а – последовательное; б – параллельное;

в – по схеме с замкнутой обратной связью

Если сигнал с выхода обратной связи и основной входной сигнал соединения действуют в одном направлении, то обратная связь называется положительной, а если эти сигналы действуют в противоположных направлениях – отрицательной.

Комбинации этих соединений звеньев позволяют представить любую сложную АСР. По передаточным функциям звеньев могут быть найдены передаточные функции систем.

Выше рассматривались звенья и соединения только с одной входной и одной выходной величинами. Однако большое число реальных объектов, а также систем регулирования обычно представляют собой соединения звеньев, имеющих несколько входных и выходных величин. Такие соединения имеют несколько каналов прохождения сигналов.

В табл. 6.2 приведены уравнения динамики типовых динамических звеньев, их переходные характеристики и графики, а в табл. 6.3 – их передаточные функции.

Таблица 6.2. Основные характеристики типовых динамических

звеньев

Звено	Уравнение динамики и переходная характеристика	График переходной характеристики
Усилительное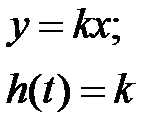
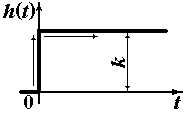
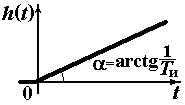
Интегрирующее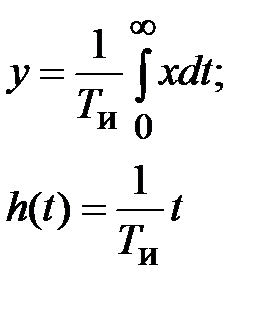
Дифференцирующее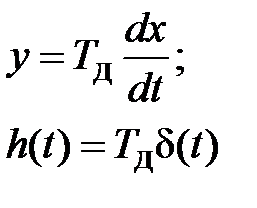
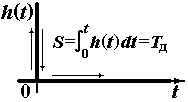
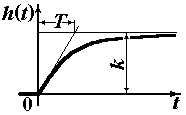
Апериодическое 1-го порядка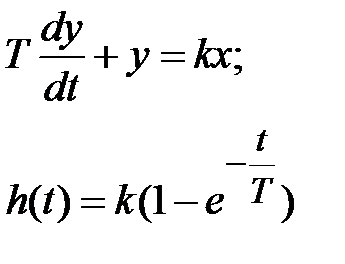
Колебательное	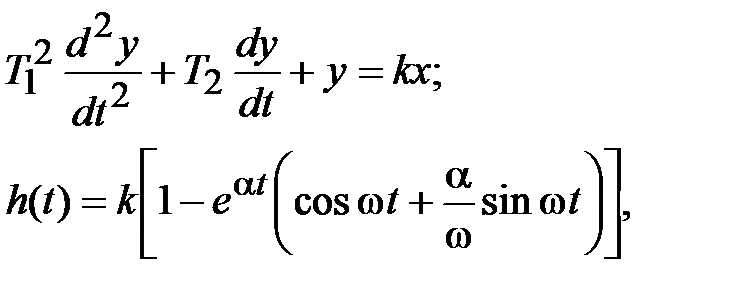где
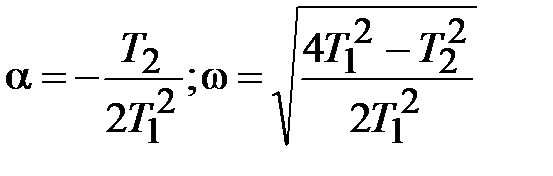
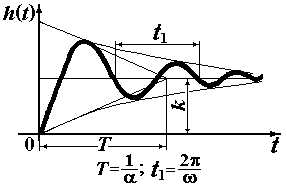
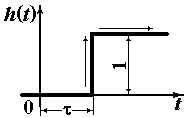
Запаздываю-щее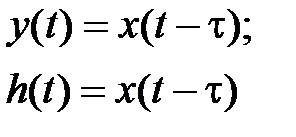

Таблица 6.3. Передаточные функции и частотные характеристики типовых динамических звеньев

Звено	Передаточная функция	Характеристика
амплитудно-частотная	фазо-частотная	амплитудно-фазовая
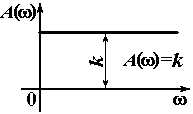
Усилительное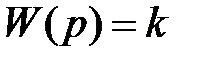
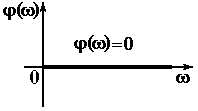
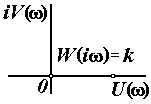
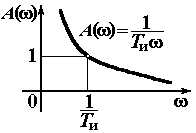
Интегрирующее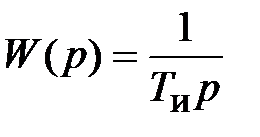
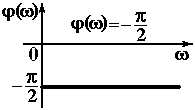
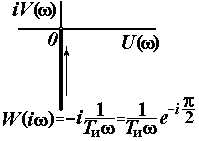
Дифференцирующее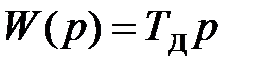

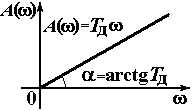
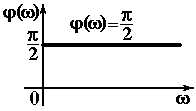
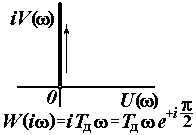
Окончание табл. 6.3

Звено	Передаточная функция	Характеристика
амплитудно-частотная	фазо-частотная	амплитудно-фазовая
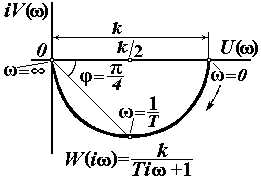
Апериодическое 1-го порядка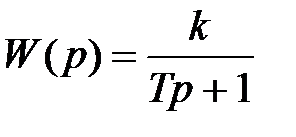
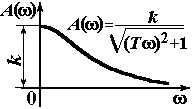
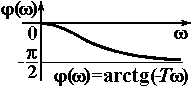
Колебательное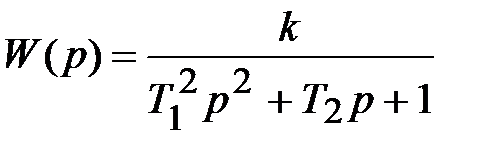
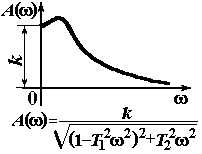
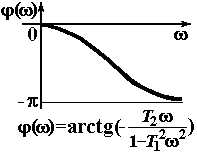
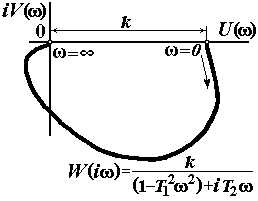
Запаздывающее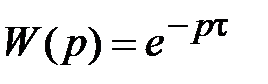

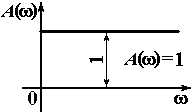
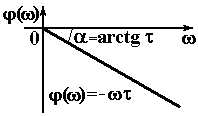
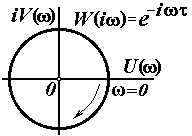
Для нахождения передаточной функции системы W(p), состоящей из п последовательно соединенных звеньев, передаточные функции которых соответственно обозначены через W₁(p), W₂(p), ..., W_n(p) (см. рис. 6.12, а), напишем для каждого ее звена уравнение, подобное уравнению (6.14)

Y₁(p) = W₁(p)X₁(p) = W₁(p)X(p);

Y₂(p) = W₂(p)X₂(p) = W₂(p) Y₁(p);

………………… (6.38)

Y(p) = Y_n(p) = W_n(p)X_n(p) = W_n(p)Y_n-1(p).

Исключим из системы (6.38) промежуточные величины

Y(p) = [W₁(p)×W₂(p)×…×W_n(p)]X(p).

Сравнивая полученное с уравнением (6.14), найдем

W(p) = W₁(p)×W₂(p)×…×W_n(p) = 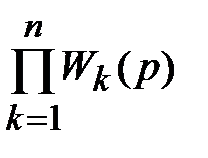. (6.39)

Таким образом, при последовательном соединении звеньев передаточная функция системы равна произведению передаточных функций входящих в нее звеньев.

Для нахождения передаточной функции системы W(p), составленной из п параллельно соединенных звеньев, передаточные функции которых соответственно равны W₁(p), W₂(p), ..., W_n(p) (см. рис. 6.12, б), определим Лапласовы изображения выходных величин всех звеньев системы:

X(p) = X₁(p) = X₂(p) = … = X_n(p);

Y₁(p) = W₁(p)X(p);

Y₂(p) = W₂(p)X(p);

………………… (6.40)

Y_n(p) = W_n(p)X(p).

Запишем в изображениях уравнение (6.36) для суммирующего звена

Y(p) = Y₁(p) + Y₂(p) + … + Y_n(p).

Подставляя выражения для Y₁(p),×Y₂(p),…, Y_n(p) и т.д. в полученное уравнение, имеем

Y(p) = [W₁(p) + W₂(p) + … + W_n(p)]X(p). (6.41)

Сравнивая уравнения (6.14) и (6.41), окончательно получим

W(p) = W₁(p) + W₂(p) + … + W_n(p) = 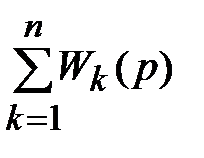. (6.42)

Таким образом, при параллельном соединении звеньев передаточная функция системы равна сумме передаточных функций входящих в нее звеньев.

Для нахождения передаточной функции соединения с замкнутой обратной связью (структурную схему см. на рис. 6.12, в) относительно величины Y введем следующие обозначения: W₁(p) – передаточная функция цепочки звеньев прямой связи; W₂(p) – передаточная функция цепочки звеньев обратной связи. Тогда передаточные функции W₁(p) и W₂(p) можно выразить

W₁(p) = Y(p)/X₁(p); (6.43)

W₂(p) = Y₂(p)/Y(p). (6.44)

При положительной обратной связи, когда сигналы прямой и обратной связей складываются, для суммирующего узла

X₁(p) = X(p)+Y₂(p). (6.45)

Из уравнений (6.43) и (6.44) найдем соответственно величины X₁(p) и Y₂(p):

X₁(p) = Y(p)/W₁(p);

Y₂(p) = W₂(p)Y(p).

Подставляя полученные выражения в уравнение (6.45), имеем

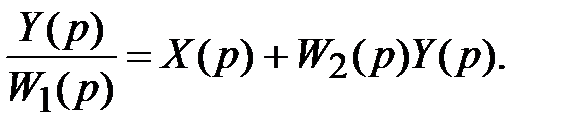
Сгруппируем в левой части члены, содержащие Y(p):

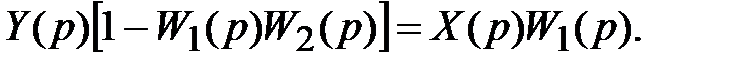
Из последнего равенства найдем отношение Y(p)/X(p), которое и является искомой передаточной функцией:

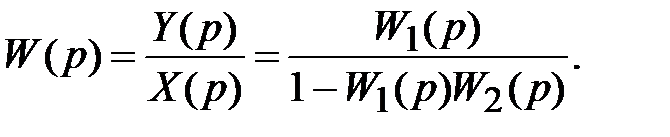(6.46)

Таким образом, передаточная функция соединения с замкнутой положительной обратной связью представляет собой дробь, числитель которой равен передаточной функции цепочки звеньев прямой связи, а знаменатель – выражению: единица минус произведение передаточных функций цепочек прямой и обратной связей (или единица минус передаточная функция соединения в разомкнутом состоянии).

Для нахождения передаточной функции соединения с замкнутой отрицательной обратной связью, в котором сигналы прямой и замыкающей обратной связей вычитаются, можно воспользоваться уравнением (6.46) при условии изменения знака минус в знаменателе на плюс:

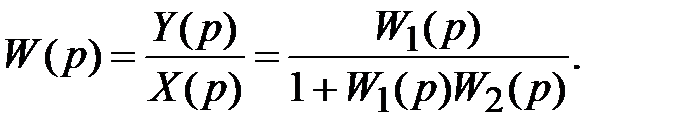(6.47)

Однако следует иметь в виду, что при расчете систем указанные знаки в знаменателе передаточных функций соединений (6.46) и (6.47) должны определяться с учетом знаков передаточных функций звеньев, входящих в эти соединения.

Аналогичным образом может быть найдено выражение для передаточной функции соединения с замкнутой обратной связью относительно любой промежуточной величины.

Характеристические уравнения. Знаменатель передаточной функции системы характеризует ее внутренние динамические свойства, отражает ее поведение в свободном состоянии; полином знаменателя D(р) называют характеристическим. Согласно уравнению (6.17) для системы n-го порядка

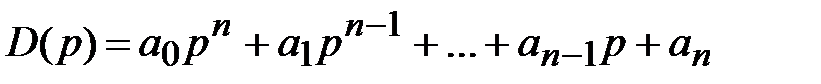. (6.48)

Знаменатель передаточной функции системы или характеристический полином, приравненный нулю, представляет характеристическое уравнение системы, которое имеет вид:

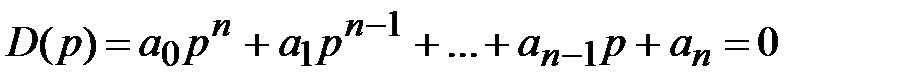. (6.49)

Характеристические полиномы и характеристические уравнения служат исходным материалом при исследовании систем на устойчивость.