Численные методы решения систем линейных уравнений

Основные вопросы, рассматриваемые на лекции:

1. Метод простой итерации.

2. Метод Зейделя.

3. Метод исключения Гаусса.

1. Метод простой итерации

Пусть дана система линейных уравнений 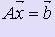(1),
где
Предполагая, что a_ii 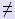0 (i = 1, :,n) разрешим её относительно x₁, x₂,:, x_n:
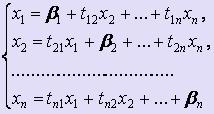(2),
где β_i = b_i / a_ii, t_ij = -a_ij / a_ii, при i 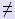j, t_ij = 0 при i = j.
Систему (2) можно записать в виде 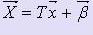( 2' ).

Теорема. Если матрица Т удовлетворяет одному из условий:
с ,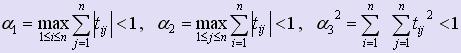
то система уравнений (2) имеет единственное решение, которое может быть получено как предел последовательности, построенной по формулам 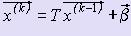, k = 1, 2, :, начиная с произвольного x⁽⁰⁾ = ( x₁⁽⁰⁾, x₂⁽⁰⁾, :, x_n⁽⁰⁾ ).
Процесс уточнения корня заканчивается, когда выполняется условие 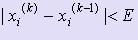,i = 1, :, n, где E - допустимая погрешность вычисления. При этом x^(k) = ( x₁^(k), x₂^(k), :, x_n^(k) ) - решение системы (1).

· Метод Зейделя

Пусть дана система линейных уравнений (1). Сведём систему (1) к системе (2). Зададим некоторые начальные приближения неизвестных x₁⁽⁰⁾ = β₁, x₂⁽⁰⁾ = β₂, :, x_n⁽⁰⁾ = β_n.
Подставим их в правые части системы и вычислим новые приближения, при этом будем использовать приближения к решениям, найденные при выполнении текущей итерации, т.е.

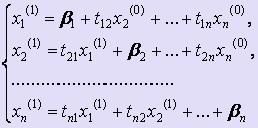
Аналогичным образом проводим вторую итерацию и т.д.
Процесс уточнения корня заканчивается, когда выполняется условие 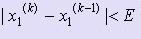,k = 1, :, n, где E - допустимая погрешность вычисления.
Замечание: при решении системы линейных уравнений методом Зейделя итерационный процесс будет сходящимся лишь в случае, если для каждого уравнения выполняется условие 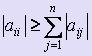, i = 1, :, n, однако в сумму не входит слагаемое a_ij c равными i и j. При этом хотя бы одно неравенство должно выполняться строго. Это условие является достаточным условием сходимости метода Зейделя.

· Метод исключения Гаусса

(рассматривается решение систем уравнений данным методом и вычислений обратной матрицы с помощью метода Гаусса).

Метод исключения Гаусса относится к прямым методам решения систем линейных уравнений.
Идея этого метода заключается в том, чтобы исходную систему линейных уравнений 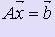(1) с произвольной матрицей А свести некоторыми эквивалентными преобразованиями к системе вида 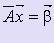(2), где Ā - треугольная матрица.
Затем из последнего уравнения системы (2) находится x_n, из предыдущего - x_n-1 и т.д.
Вычисление обратной матрицы с помощью метода Гаусса:
Пусть x_i - i-ый столбец искомой обратной матрицы, e_i - i-ый столбец единичной матрицы.
Т.к. A · A^-1 = E, то 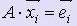, при i = 1, 2, :, n. Задача нахождения обратной матрицы сводится к задаче решения n систем n линейных уравнений с одной и той же матрицей A, но с разными правыми частями.