Частотные характеристики

Еще один популярный эталонный сигнал – гармонический (синус, косинус), например

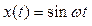, (23)

где ω – угловая частота (в радианах в секунду). Можно показать, что при таком входе на выходе линейной системы в установившемся режиме (при больших t) будет синус той же частоты, но с другой амплитудой A и сдвигом фазы φ

.

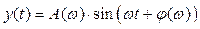Для каждой частоты входного сигнала будет своя амплитуда и свой сдвиг фазы. Чтобы определить по графику фазовый сдвиг φ, нужно найти расстояние Δt по оси времени между соответствующими точками синусоид (например, точками пересечения с осью t или вершинами). Если Δt умножить на частоту ω, получаем сдвиг фазы φ (в радианах).

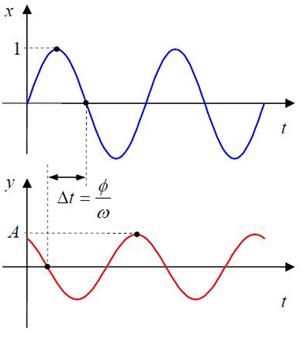
На рисунке показан случай φ > 0 (опережение по фазе), когда выход сдвинут «влево» по оси времени относительно входа, то есть, «идет раньше» входного. Зная передаточную функцию системы W(s), можно вычислить амплитуду и сдвиг фазы по формулам

.

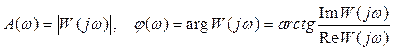Для каждой частоты ω значение 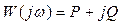– это некоторое комплексное число, имеющее амплитуду 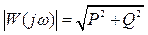и фазу .

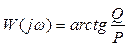Функция W(jω) называется частотной характеристикойзвена, поскольку она характеризует выход системы при гармонических сигналах разной частоты. Зависимости P(ω) и Q(ω) (вещественная и мнимая части W(jω)) – это вещественная и мнимая частотные характеристики.

Функции A(ω) и φ(ω) (они для каждой частоты принимают вещественные значения) называются соответственно амплитуднойи фазовой частотными характеристиками(АЧХ и ФЧХ). Амплитудная частотная характеристика – это коэффициент усиления гармонического сигнала. Если на какой-то частоте ω значение A(ω) > 1, входной сигнал усиливается, если A(ω) < 1, то вход данной частоты ослабляется.

По форме АЧХ различают несколько основных типов звеньев:

1) фильтр низких частот – пропускает низкочастотные сигналы примерно с одинаковым коэффициентом усиления, блокирует высокочастотные шумы и помехи;

2) фильтр высоких частот – пропускает высокочастотные сигналы, блокирует сигналы низкой частоты;

3) полосовой фильтр – пропускает только сигналы с частотами в полосе от ω₁ до ω₂;

4) полосовой режекторный фильтр – блокирует только сигналы с частотами в полосе от ω₁ до ω₂, остальные пропускает.

На рисунке показаны амплитудные частотные характеристики идеальных фильтров этих четырех типов.

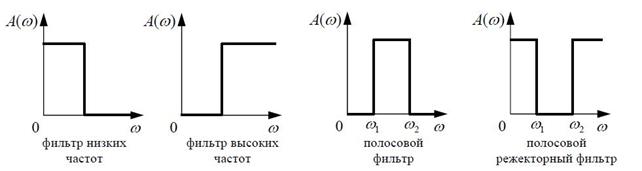
В радиотехнике используется понятие полосы пропускания – это ширина полосы частот, в которой значение АЧХ больше, чем 1/ 2 от ее максимального значения.

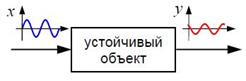
Частотные характеристики во многих случаях можно снять экспериментально. Если объект устойчивый, на его вход подается гармонический сигнал (23) и записывается сигнал y(t) на выходе. Определив амплитуду и сдвиг фазы для разных частот, можно построить по точкам амплитудную и фазовую частотные характеристики.

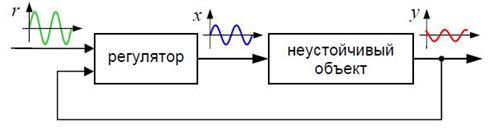
Если объект неустойчив, то при подаче на вход синуса амплитуда колебаний на выходе будет неограниченно расти. Однако частотную характеристику все равно можно определить экспериментально. Для этого нужно сначала найти какой-нибудь регулятор, который сделает замкнутую систему устойчивой. Затем на вход r(t) подают синусоидальный сигнал и сравнивают сигналы x(t) и y(t) на входе и выходе интересующего нас объекта, определяя для каждой частоты ω «коэффициент усиления» A(ω) (отношение амплитуд сигналов x(t) и y(t) ) и сдвиг фазы φ(ω).