Числа в форме с плавающей запятой

От недостатков чисел с ФЗ в значительной степени свободна форма представления чисел с плавающей запятой (ПЗ), известная также под названиями нормальной или полулогарифмической формы. В данном варианте каждое число разбивается на две группы цифр. Первая группа цифр называется мантиссой, вторая - порядком.

Число представляется в виде произведения 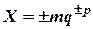, где m- мантисса числа X, р — порядок числа, q — основание системы счисления.

Для представления числа в форме с ПЗ требуется задать знаки мантиссы и порядка, их модули в q - ичном коде, а также основание системы счисления (рис. 5.4). Нормальная форма неоднозначна, так как взаимное изменение m приводит к «плаванию» запятой, чем и обусловлено название этой формы.

Рис. 5.4.Форма представления чисел с плавающей запятой

Диапазон и точность представления чисел с ПЗ зависят от числа разрядов, отводимых под порядок и мантиссу. На рис. 5.5. показаны диапазоны разрядностей порядка и мантиссы, характерные для известных ВМ.

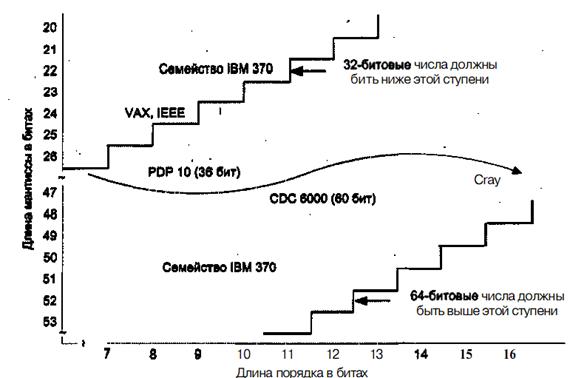
Рис. 5.5. Типовые разрядности полей порядка и мантиссы

Помимо разрядности порядка и мантиссы диапазон представления чисел зависит и от основания используемой системы счисления, которое может быть отличным от 2. Например, в универсальных ВМ (мэйнфреймах) фирмы IBM используется база 16. Это позволяет при одинаковом количестве битов, отведенных под порядок, представлять числа в большем диапазоне. Так, если поле порядка равно 7 битам, максимальное значение, на которое умножается мантисса, равно 2¹²⁸(при 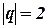) или 16 ¹²⁸(при 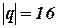), а диапазоны представления чисел соответственно составят 10^-19 < |Х| < 10⁺¹⁹ и 10^-76 < |Х| < 10⁺⁷⁶ . Известны также случаи использования базы 8, например, в ВМ В-5500 фирмы Burroughs.

В большинстве вычислительных машин для упрощения операций над порядками последние приводят к целым положительным числам, применяя так называемый смещенный порядок. Для этого к истинному порядку добавляется целое положительное число — смещение (рис. 5.6.). Например, в системе со смещением 128 порядок -3 представляется как 125 (-3 + 128). Обычно смещение выбирается равным половине представимого диапазона порядков. Отметим, что смещенный порядок занимает все биты поля порядка, в том числе и тот, который ранее использовался для записи знака порядка.

Рис. 5.6. Формат числа с ПЗ со смещенным порядком

Мантисса в числах с ПЗ обычно представляется в нормализованной форме. Это означает, что на мантиссу налагаются такие условия, чтобы она по модулю была меньше единицы ( 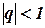), а первая цифра после точки отличалась от нуля. Полученная таким образом мантисса называется нормализованной. Для применяемых в ВМ систем счисления можно записать:

· двоичная: Х = q2^p (1 > 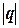- 1/2);

· восьмеричная: X = q8^p (1 > 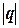-1/8)

· шестнадцатеричная: X = q16^p 1 > 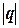- 1/16).

Если первые i цифр мантиссы равны нулю, для нормализации ее нужно сдвинуть относительно запятой на i разрядов влево с одновременным уменьшением порядка на i единиц. В результате такой операции число не изменяется.

В примере для шестнадцатеричной системы после нормализации старшая цифра в двоичном представлении содержит впереди три нуля (0001). Это несколько уменьшает точность представления чисел по сравнению с двоичной системой при одинаковом числе двоичных разрядов, отведенных под мантиссу.

Если для записи числа с ПЗ используется база 2 (q = 2), то часто применяют еще один способ повышения точности представления мантиссы, называемый приемом скрытой единицы. Суть его в том, что в нормализованной мантиссе старшая цифра всегда равна единице (для представления нуля используется специальная кодовая комбинация), следовательно, эта цифра может не записываться, а подразумеваться. Запись мантиссы начинают с ее второй цифры, и это позволяет задействовать дополнительный значащий бит для более точного представления числа.

Следует отметить, что значение порядка в данном случае не меняется. Скрытая единица перед выполнением арифметических операций восстанавливается, а при записи результата — удаляется. Таким образом, нормализованная мантисса 0,101000(1) при использовании способа «скрытой единицы» будет иметь вид 0,010001 (в скобках указана цифра, не поместившаяся в поле мантиссы при стандартной записи).

Для более существенного увеличения точности вычислений под число отводят несколько машинных слов, например два. Дополнительные биты, как правило, служат для увеличения разрядности мантиссы, однако в ряде случаев часть из них может отводиться и для расширения поля порядка. В процессе вычислений может получаться ненормализованное число. В таком случае ВМ, если это предписано командой, автоматически нормализует его.

Рассмотренные принципы представления чисел с ПЗ поясним на примере. На рис. 5.7. представлен типичный 32-битовый формат числа с ПЗ. Старший (левый) бит содержит знак числа. Значение смещенного порядка хранится в разрядах с 1-г о по 8-й и может находиться в диапазоне от 0 до 255. Для получения фактического значения порядка из содержимого этого поля нужно вычесть фиксированное значение, равное 128. С таким смещением фактические значения порядка могут лежать в диапазоне от -128 до +127. В примере предполагается, что основание системы счисления равно 2. Третье поле слова содержит нормализованную мантиссу со скрытым разрядом (единицей). Благодаря такому приему 23-разрядное поле позволяет хранить 24-разрядную мантиссу в диапазоне oт 0,5 до 1,0 .

Рис. 5.7. Типичный 32-битовый формат числа с плавающей запятой

На рис. 5.8. приведены диапазоны чисел, которые могут быть записаны с помощью 32-разрядного слова.

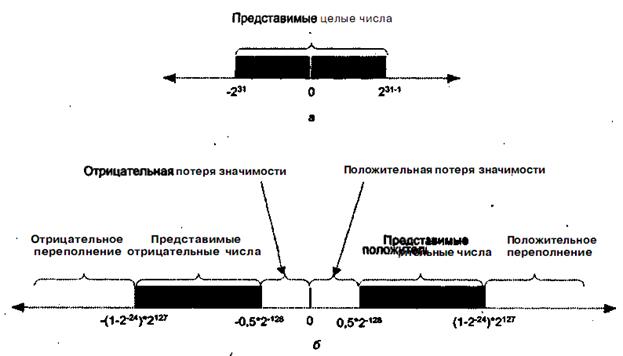
Рис. 5.8. Числа, представимые в 32-битовых форматах: а — целые числа с фиксированной запятой; б - числа с плавающей запятой

В варианте с ФЗ для целых чисел в дополнительном коде могут быть представлены все целые числа от -2³¹ до 2³¹ – 1, то есть всего 2³² различных чисел (см. рис. 5.8, а). Для случая ПЗ возможны следующие диапазоны чисел (см. рис. 5.8, б).

· отрицательные числа между -(1 – 2^-24 ) х 2¹²⁷ и - 0,5 х 2¹²⁸ ;

· положительные числа между 0,5 х 2^-128 и (1 – 2²⁴) х 2¹²⁷.

В эту область не включены пять участков:

· отрицательные числа, меньшие чем -(1 – 2^-24) х 2¹²⁷ - отрицательное переполнение;

· отрицательные числа, большие чем -0,5 х 2¹²⁸ - отрицательная потеря значимости;

· положительные числа, меньшие чем 0,5 х 2^-128 - положительная потеря значимости;

· положительные числа, большие чем (1 – 2²⁴) х 2¹²⁷ - положительное переполнение.

Показанная запись числа с ПЗ не учитывает нулевого значения. Для этой цели используется специальная кодовая комбинация. Переполнения возникают, когда в результате арифметической операции получается значение большее, чем можно представить порядком 127 (2¹²⁰ х 2¹⁰⁰ = 2²²⁰ ). Потеря значимости — это когда результат представляет собой слишком маленькое дробное значение (2^-120 х 2^-100 = 2^-220). Потеря значимости является менее серьезной проблемой, поскольку такой результат обычно рассматривают как нулевой.

Следует также отметить, что числа в форме с ПЗ, в отличие от чисел в форме с ФЗ , размещены на числовой оси неравномерно. Возможные значения в начале числовой оси расположены плотнее, а по мере движения вправо — все реже (рис. 5.9.). Это означает, что многие вычисления приводят к результату, который не является точным, то есть представляет собой округление до ближайшего значения, представимого в данной форме записи.

Рис. 5.9. Плотность чисел с плавающей запятой на числовой оси

Для формата, изображенного на рис. 5.7. имеет место противоречие между диапазоном и точностью. Если увеличить число битов, отведенных под порядок, расширяется диапазон представимых чисел. Однако, Поскольку может быть представлено только фиксированное число различных значений, уменьшается плотность и тем самым точность. Единственный путь увеличения как диапазона, так и точности — увеличение количества разрядов, поэтому в большинстве ВМ предлагается использовать числа в одинарном и двойном форматах. Например, число одинарного формата может занимать 32 бита, а двойного - 64 бита.

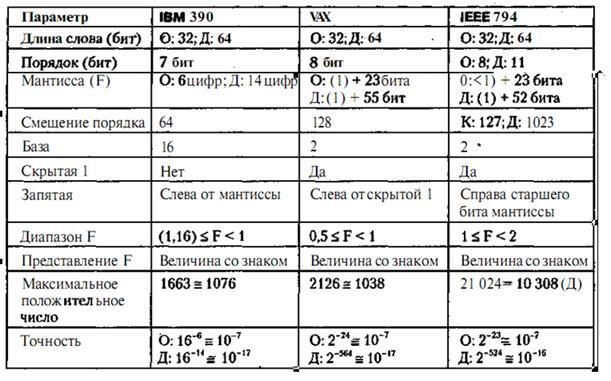
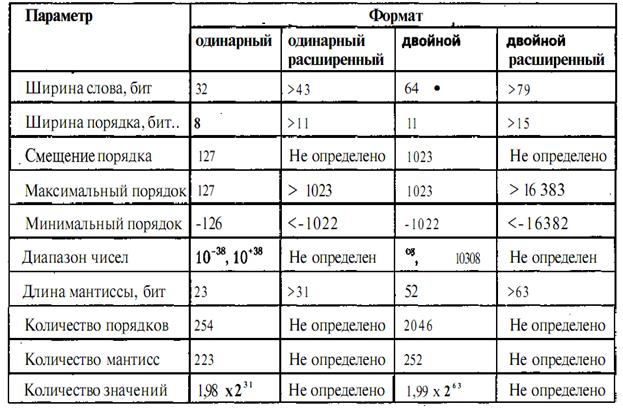
Числа с плавающей запятой в разных ВМ имеют несколько различных форматов. В табл. 5.1. приводятся основные параметры для нескольких систем представления чисел в форме с ПЗ. В настоящее время для всех ВМ рекомендован стандарт, разработанный общепризнанным международным центром стандартизации IEEE (Institute of Electrical and Electronics Engineers).

Таблица 5.1.Варианты форматов чисел с плавающей запятой

Стандарт IEEE 754

Рекомендуемый для всех ВМ формат представления чисел с плавающей запятой определен стандартом IEEE 754. Этот стандарт был разработан с целью облегчить перенос программ с одного процессора на другие и нашел широкое применение практически во всех процессорах и арифметических сопроцессорах.

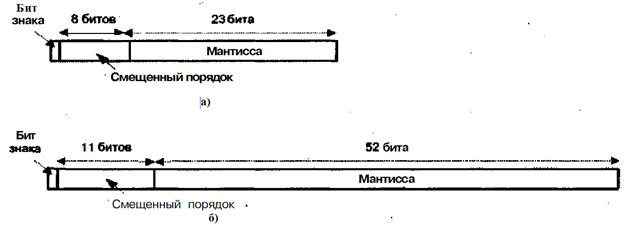
Рис. 5.10. Основные форматы IEEE754: а - одинарный; б – двойной

Стандарт определяет 32-битовый (одинарный) и 64-битовый (двойной) форматы (рис. 5.10) с 8- и 11-разрядными порядком соответственно. Основанием системы счисления является 2. В дополнение, стандарт предусматривает два расширенных формата, одинарный и двойной, фактический вид которых зависит от конкретной реализации. Расширенные форматы предусматривают дополнитель ные биты для порядка (увеличенный диапазон) и мантиссы (повышенная точность). Таблица5.2 содержит описание основных характеристик всех четырех форматов.

Не все кодовые комбинации в форматах IEEE интерпретируются обычным путем — некоторые комбинации используются для представления специальных значений. Предельные значения порядка, содержащие все нули (0) и все единицы (255 — в одинарном формате и 2047 — в двойном формате), определяют специальные значения.

Таблица 5.2.Параметры форматов стандарта IEEE754

Представлены следующие классы чисел:

· Порядки в диапазоне от 1 до 254 для одинарного формата и от 1 до 2036 — для двойного формата, используются для представления ненулевых нормализованных чисел. Порядки смещены так, что их диапазон составляет от -126 до +127 для одинарного формата и от -1022 до +1023 - для двойного формата. Нормализованное число требует, чтобы слева от двоичной запятой был единичный бит. Этот бит подразумевается, благодаря чему обеспечивается эффективная ширина мантиссы, равная 24 битам для одинарного и 53 битам — для двойного форматов.

· Нулевой порядок совместно с нулевой мантиссой представляют положительный или отрицательный 0, в зависимости от состояния бита знака мантиссы.

· Порядок, содержащий единицы во всех разрядах, совокупно с нулевой мантиссой представляют положительную или отрицательную бесконечность, в зависимости от состояния бита знака, что позволяет пользователю самому решить, считать ли это ошибкой или продолжать вычисления со значением, равным бесконечности.

· Нулевой порядок в сочетании с ненулевой мантиссой представляют ненормализованное число. В этом случае бит слева от двоичной точки равен 0 и фактический порядок равен -126 или -1022. Число является положительным или отрицательным в зависимости от значения знакового бита.

· Кодовая комбинация, в которой порядок содержит все единицы, а мантисса не равна 0, используется как признак «не числа» (NAN — Not a Number) и служит для предупреждения о различных исключительных ситуациях.