Применение метода ветвей и границ для задачи коммивояжера

Алгоритм Литла, Мурти, Суини и Кэрол для решения задачи коммивояжера также хорошо укладывается в указанную выше схему.

Поясним это подробнее, так как алгоритм Литла применяется не к целочисленной линейной модели, а к задаче коммивояжера в ее комбинаторной записи (мы излагаем несколько усовершенствованный вариант алгоритма). Напомним предварительно, что задача коммивояжера тесно связана с задачей о назначении, которая формулируется следующим образом. Задана матрица 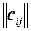размером ( 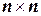). Выбрать в ней 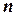элементов таким образом, чтобы а) никакие два элемента не лежали в одной строке или в одном столбце и б) сумма 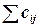, соответствующая выбранным элементам, была бы минимальной.

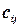Упорядоченные пары , соответствующие выбранным элементам , можно (в терминах задачи коммивояжера) интерпретировать как «поездки» из города 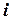непосредственно в город 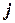. Разница же заключается в том, что в задаче о назначении не исключены петли (назначение элементов ) и подциклы. Иначе говоря, здесь не гарантируется связность маршрута. Петли можно устранить, положив для всех 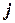. С устранением же подциклов дело обстоит сложнее. Во всяком случае задачу о назначении можно рассматривать как релаксацию задачи коммивояжера (релаксировано условие связности маршрута). В то же время задача о назначении эффективно решается известными методами.

Теперь мы можем изложить модифицированный алгоритм Литла и др.

Шаг 1. Стандартный.

Шаг 2. Стандартный.

Шаг 3. Стандартный (разные варианты этого шага в разных вариантах алгоритма).

Шаг 4. Релаксация условия связности маршрута (переход от задачи коммивояжера к соответствующей задаче о назначении).

Шаг 5. Решение задачи о назначении, полученной в пункте 4.

Шаги 6, 7, 8 — стандартные.

Шаг 9. Всегда переход к шагу 11.

Шаг 10. Пропускается.

Шаг 11. Дихотомия текущей задачи-кандидата. Выбирается пара и разветвляется на две задачи-потомка: задача, в которой из города 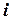обязательна поездка в город 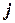. При переходе от матрицы текущей задачи-кандидата к матрице этой задачи-потомка все элементы строки 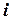и столбца 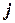, кроме , заменяются на +∞; задача, в которой из города 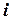запрещается поездка в город 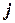. При переходе от матрицы текущей задачи-кандидата к матрице этой задачи-потомка элемент . заменяется на +∞.

Шаг 12. Стандартный.

Пример 6.1. Решение задачи коммивояжера методом ветвей и границ.

Если решать задачу коммивояжера путем полного перебора вариантов, то для нахождения оптимального маршрута объезда городов надо перебрать вариантов по критерию минимальных стоимости, времени или длины маршрута. При достаточно больших на полный перебор вариантов требуется слишком много времени.

Более эффективно задача коммивояжера решается методом ветвей и границ. Множество всевозможных решений представляется в виде дерева – связного графа, не содержащего циклов и петель. Корень дерева объединяет все множество вариантов, а вершины дерева каждого уровня содержат два непересекающихся множества: и 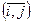. Вершина соответствует подмножеству всех маршрутов, содержащих ребро (множество неупорядочено); вершина 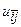- подмножеству всех маршрутов, где это ребро отсутствует. Ветвятся не все вершины дерева. В начале проводится оценка каждой вершины данного уровня (начиная с первого), и ветвится та вершина, которая получает лучшую оценку в соответствии с выбранным критерием.

Поясним изложенный выше метод на примере нахождения оптимального маршрута коммивояжера при объезде четырех городов, в каждый из которых можно попасть из каждого в соответствии с схемой (рис. 6.2).

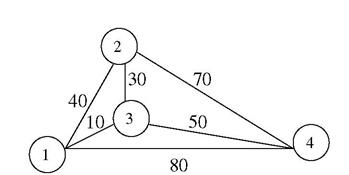
Рис. 6.2. Схема возможных маршрутов коммивояжера.

Возле соответствующих ребер даны расстояния между городами в километрах. Требуется определить кратчайший маршрут, который позволит побывать в каждом из городов по одному разу.

Расстояния между городами зададим в виде матрицы (табл. 6.1). Если ребро отсутствует, то его длина задается равной .

На первом этапе решения определим нижнюю границу оценки множества возможных маршрутов. Для этого проведем операцию редукции матрицы по строкам и столбцам. В каждой строке матрицы определим минимальный элемент и вычтем его из всех элементов (табл. 6.2 – 6.3 ).

Таблица 6.1.

Ребра графа

Таблица 6.2. Таблица 6.3.

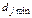
Затем аналогичную процедуру проведем по столбцам (табл. 6.4).

Таблица 6.4.

			0(10)
	0(10)

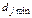
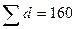
В результате мы получим полностью редуцированную матрицу (табл. 6.4), где величины и называют константами приведения. Сумма констант приведения определяет нижнюю границу оценки.

Далее определяем ребро , исключение которого максимально увеличит нижнюю границу, и разобьем все множество маршрутов относительно этого ребра на два подмножества и . С этой целью, для всех клеток матрицы с нулевыми элементами, заменяем поочередно нули на и определяем для них сумму констант приведения. Наибольшая сумма констант приведения равна 10 для ребра (табл. 6.4). Следовательно, множество всех маршрутов разбивается на подмножества и (рис. 6.3).

Рис. 6.3. Дерево маршрутов после первого этапа ветвления.

Исключение ребра проводим путем замены элемент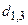а на , после чего осуществляем операцию редукции полученной матрицы (табл. 6.5– 6.6).

Таблица 6.5. Таблица 6.6.

0

0

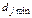
Сумма констант приведения сокращенной матрицы равна 10. Нижняя граница оценки цикла равна 160+10=170.

Включение дуги осуществляется путем исключения всех элементов первой строки и третьего столбца из таблицы 6.6. Элемент 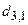заменяем на , для исключения образования негамильтонова цикла. В результате получим сокращенную матрицу 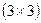, которая подлежит редукции.

Таблица 6.7. Таблица 6.8.

								0(20)

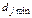
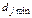
Нижняя граница оценки цикла при включении дуги также равна 160+10=170. Для определенности включим дугу и определим следующее ветвление дерева решений. Из табл. 6.8 видно, что максимальное увеличение нижней границы (+20) возможно по ребру , по которому и организуем следующее ветвление (рис. 6.4).

Рис. 6.4. Дерево маршрутов после второго этапа ветвления.

Рассмотрим исключение ветви (табл. 6.9 – 6.10).

Таблица 6.9. Таблица 6.10.

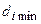
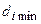
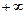
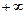
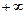
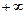
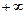
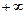
								0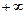

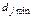
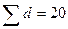
Нижняя граница оценки цикла равна 160+20=180.

Рассмотрим включение ветви 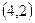(табл. 6.11). Элемент 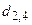заменяем на 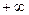. Редукция полученной матрицы не увеличивает нижнюю границу оценки, которая остается на уровне 170 ветвь 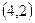включается в цикл.

Таблица 6.11.

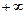
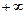
В соответствии с последней таблицей включаем в гамильтонов цикл ребра 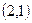и 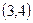. После третьего ветвление дерево маршрутов примет вид (рис. 6.5).

Рис. 6.5. Итоговое дерево маршрутов.

В соответствии с деревом ветвлений гамильтонов контур образуют ребра: 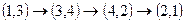. Минимальная длина маршрута равна 170 км, что совпадает с нижней границей оценки.