Релаксация Лагранжа
Релаксация Лагранжа широко используется во многих приложениях ДО. Это связано с возможностью «спрятать» «неудобные» или трудные ограничения в целевую функцию функции Лагранжа, что дает возможность получать хорошие оценки за приемлемое время.
Рассмотрим задачу ЦЛП вида
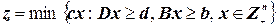 , (P)
, (P)
где ограничения 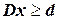 представляют «сложные» ограничения, задающие целочисленное множество
представляют «сложные» ограничения, задающие целочисленное множество 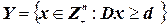 , в то время как ограничения представляют собой «более легко вычислимые» ограничения и задающие множество
, в то время как ограничения представляют собой «более легко вычислимые» ограничения и задающие множество 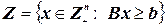 , что означает следующее:
, что означает следующее: 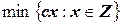 может быть легко решена.
может быть легко решена.
Релаксация Лагранжа для описанной выше задачи ЦЛП состоит в превращении ограничений 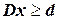 в ограничения, которые могут быть нарушены со штрафом
в ограничения, которые могут быть нарушены со штрафом 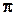 , в то время как остальные ограничения, описывающие множество
, в то время как остальные ограничения, описывающие множество 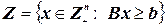 , сохраняются. Это приводит к постановке так называемой лагранжевой подзадачи:
, сохраняются. Это приводит к постановке так называемой лагранжевой подзадачи:
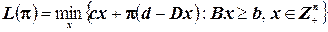 ,
,
которая, согласно предположению, является относительно легко разрешимой. Для любого неотрицательного штрафного вектора 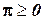 так называемая двойственная функция
так называемая двойственная функция 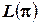 задает нижнюю границу для оптимального значения целевой функции
задает нижнюю границу для оптимального значения целевой функции 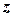 задачи ЦЛП (P). Действительно, оптимальное решение
задачи ЦЛП (P). Действительно, оптимальное решение 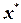 задачи (P) удовлетворяет условиям
задачи (P) удовлетворяет условиям 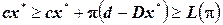 .
.
Наилучшей из этих нижних границ является 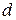 , которая получается с помощью решения двойственной задачи Лагранжа:
, которая получается с помощью решения двойственной задачи Лагранжа:
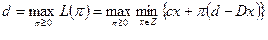 .
.
6.2. Применение метода ветвей и границ для решения задач дискретной оптимизации
6.2.1. Метод Ленд и Дойг для задачи частично целочисленного линейного программирования.
Продемонстрируем, как конкретные методы и алгоритмы вписываются в описанную выше схему, взяв в качестве примера алгоритм Лэнд и Дойг в том виде, как он изложен у Джеффриона и Марстена[6].
Шаг 1. Стандартный (в список заносится исходная задача (6.1) – (6.4)).
Шаг 2. Стандартный.
Шаг 3. Одностороннее ветвление (т. е. в списке задач-кандидатов для ветвления выбирается в первую очередь одна из задач-потомков только что разветвленной ЗК).
Шаг 4. Релаксация всех условий целочисленности.
Шаг 5. Применение алгоритма линейного программирования.
Шаги 6, 7, 8 — стандартные.
Шаг 9. Всегда переход к шагу 11.
Шаг 10. Пропускается.
Шаг 11. Дихотомия текущей задачи-кандидата:
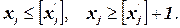
Здесь 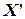 ‑ оптимальное нецелочисленное решение задачи линейного программирования, полученное на шаге 5.
‑ оптимальное нецелочисленное решение задачи линейного программирования, полученное на шаге 5.
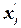 ‑ одна из нецелочисленных компонент
‑ одна из нецелочисленных компонент 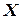 ,
, 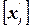 ‑ целая часть от
‑ целая часть от 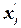 .
.
Шаг 12. Стандартный.
Дата добавления: 2016-06-05; просмотров: 2117;










