Детерминированные машины Тьюринга и класс Р

Детерминированная машина Тьюринга (ДМТ) состоит из управляющего устройства с конечным числом состояний, читающей/пишущей головки, которая может считывать и записывать символы в ячейки, и неограниченной в обе стороны ленты, разделенной на бесконечное число одинаковых ячеек, занумерованных целыми числами. ДМТ-программа определяется следующими компонентами:

— конечным множеством 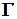символов, которые записываются на ленте, подмножеством 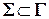входных символов и выделенным пустым символом ;

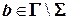— конечным множеством состояний 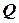, в котором выделены начальное состояние 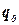и два заключительных состояния: 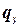и ;

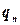— функцией переходов

.

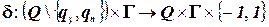Работа ДМТ-программы определяется следующим образом. Входом для программы является слово 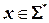, которое записывается в ячейки с номерами 1, 2, ..., |х| по одному символу в ячейку. Все остальные ячейки в начальный момент времени содержат символ 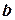. Программа начинает работу в состоянии 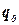а головка находится над ячейкой с номером 1.

Процесс вычислений осуществляется последовательно шаг за шагом.

Один шаг вычислений ДМТ-программы состоит из следующих действий:

— если текущее состояние есть 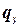или 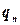то процесс вычислений заканчивается с результатом соответственно «да» или «нет»;

— в противном случае головка считывает из ячейки некоторый символ 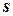вычисляет 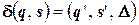, записывает на место 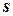символ 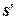, переходит в состояние 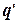, сдвигает головку на одну ячейку вправо ( 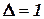) или влево ( ).

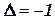Пусть 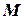‑ ДМТ-программа.

Определение 5.3. Говорят, что программа 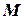принимает слово 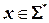, если ее применение ко входу 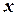приводит к остановке машины в состоянии .

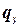Определение 5.4. Язык 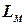является распознаваемым программой 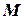, если составляющее его множество слов есть .

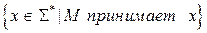Определение 5.5. Программа 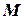называется алгоритмической, если она останавливается на всех словах входного алфавита независимо от того, принимает программа слова или нет.

Определение 5.6. Говорят, что ДМТ-программа 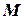решает задачу распознавания 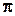при кодировании 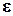, если она алгоритмическая и .

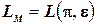Временная сложность ДМТ-программы 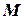определяется следующим выражением:

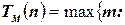существует такое слово , ,

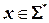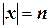что вычисление по программе 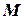для входа 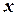требует

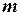шагов от начала до останова}.

Определение 5.7. Программа 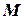называется полиномиальной ДМТ-программой, если существует полином 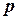такой, что для любого :

.

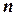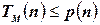Заметим, что алгоритмическая программа 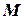может не только решать задачи распознавания, но и вычислять значения функции 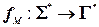. При этом значение функции 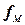для каждого входа 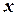определяется словом, записанным после останова машины в ячейках с номерами 1, 2, 3,..., включая последнюю непустую ячейку.

Теперь можно формально определить первый важный класс языков — класс .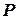

Определение 5.8. Класс языков распознавания 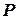состоит из языков L, для которых принадлежность к нему определяется за полиномиальное время, т.е. 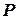= {L: существует полиномиальная ДМТ-программа 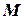для которой 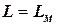}. Будем говорить, что задача распознавания 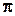принадлежит классу 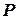при кодировании 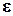, если .

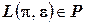5.1.7. Недетерминированные машины Тьюринга и класс

Понятие «полиномиальной проверяемости» позволяет выделить важный класс задач . Задачи этого класса решаются недетерминированными алгоритмами за полиномиальное время.

Недетерминированные алгоритмы состоят из стадии угадывания и стадии проверки. На стадии угадывания индивидуальной задаче 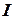ставится в соответствие (угадывается) некоторая структура 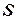. Затем 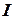и 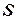вместе подаются в качестве входа на стадию проверки, которая выполняется обычным детерминированным образом и либо заканчивается получением ответа «да» или «нет», либо продолжается бесконечно.

Определение 5.9. Недетерминированный алгоритм решает задачу распознавания 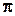, если для любой индивидуальной задачи 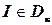выполняются следующие условия:

1. Если 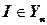, то существует такая структура 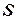, угадывание которой для входа 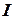приведет к тому, что стадия проверки, начиная работу на входе 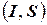, закончится ответом «да»;

2. Если 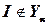, то не существует такой структуры 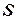, угадывание которой для входа 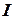обеспечило бы окончание стадии проверки на входе 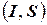с ответом «да».

Формальной моделью для недетерминированного алгоритма является программа для недетерминированной машины Тьюринга (НДМТ), которая отличается от ДМТ наличием угадывающего модуля с пишущей головкой.

Определение 5.10. Вычисление, которое осуществляет НДМТ-программа, называется принимающим, если остановка происходит в состоянии 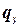. Все остальные вычисления, независимо от того, заканчивает или нет работу соответствующая НДМТ, называются непринимающими.

Отметим, что НДМТ-программа может иметь бесконечное число возможных вычислений при данном входе 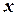, по одному для каждого слова, полученного на этапе угадывания.

Определение 5.11. Говорят, что НДМТ-программа 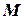принимает слово 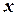, если по крайней мере одно из вычислений при входе 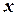является принимающим.

Определение 5.12. Язык 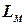, распознаваемый НДМТ-программой 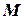, — это множество слов { 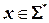| 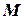принимает }.

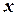Время, требующееся для того, чтобы принять слово 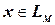, ‑ это минимальное число шагов, выполняемых на стадиях угадывания и проверки, причем минимум берется по всем принимающим вычислениям для входа .

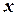Временная сложность НДМТ-программы 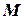определяется следующим выражением:

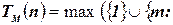существует такое слово , ,

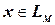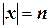что время принятия 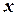программой 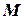равно }).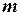

Определение 5.13. НДМТ-программа 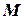называется полиномиальной (или программой с полиномиальным временем работы), если существует полином 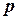такой, что для любого 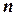имеет место неравенство .

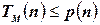Теперь можно формально определить второй важный класс языков ‑ класс . Он определяется следующим образом.

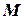Определение 5.14. Класс языков распознавания = {L: существует полиномиальная НДМТ-программа для которой 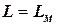}. Будем говорить, что задача распознавания 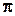принадлежит классу при кодировании 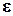, если .

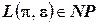Как и в случае класса 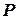, говорим, что 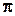принадлежит классу , не упоминая конкретную схему кодирования, в том случае, когда возможно определить некоторую разумную схему кодирования задачи 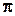, которая даст язык, принадлежащий .

Учитывая замечание о полиномиальной эквивалентности существующих моделей вычислительных устройств, будем в дальнейшем отождествлять формально определенный класс с классом всех задач распознавания, «разрешимых» недетерминированными алгоритмами с полиномиальным временем работы.

5.2. Использование теории сложности в дискретной оптимизации 5.2.1. Соотношение между классам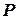и и

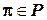
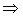
Всякий детерминированный полиномиальный алгоритм можно рассматривать как частный случай недетерминированного полиномиального алгоритма, в котором отсутствует стадия угадывания, а стадия проверки совпадает с детерминированным алгоритмом. Поэтому справедливо 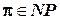, т.е. 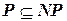. В настоящее время не удалось доказать ни одно из более сильных утверждени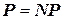й: или .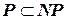

Один из результатов теории сложности сформулирован в следующей теореме.

Теорема 5.1. Если 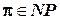, то существует такой полином 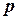, что 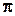может быть решена детерминированным алгоритмом с временной сложностью .

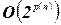5.2.2. Полиномиальная сводимость и -полные задачи

Центральное место в теории -полных задач занимает понятие полиномиальной сводимости.

Определение 5.15. Говорят, что имеет место полиномиальная сводимость языка 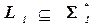к языку 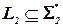, если существует функция 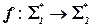, удовлетворяющая двум условиям:

— существует ДМТ-программа, вычисляющая 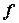с временной сложностью, ограниченной некоторым полиномом;

— для любого 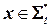, 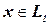в том и только том случае, когда .

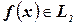Если 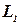полиномиально сводится к 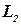, то будем писать 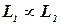и говорить « 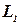сводится к 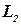» (опуская слово «полиномиально»). Важность введенного понятия «полиномиальная сводимость» вытекает из следующей теоремы.

Теорема 5.2. Если 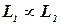, то из 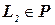следует, что 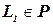(эквивалентное утверждение: из 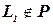следует, что ).

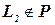Доказательство. Достаточно рассмотреть в качестве ДМТ-программы, распознающей 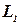композицию двух полиномиальных ДМТ-программ. Первая из них вычисляет функцию 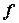, вторая распознает 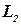. Время работы полученной программы ограничено полиномом:

,

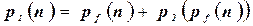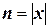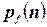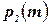где , и ‑ полиномы, ограничивающие время работы ДМТ-программы, вычисляющей 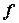и распознающей 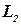соответственно ( , , .

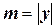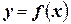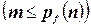Определение 5.16. Задача распознавания 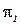полиномиально сводится к задаче распознавания 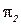( 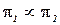), если 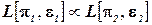. Таким образом, на уровне задач распознавания полиномиальная сводимость означает наличие функции 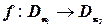, удовлетворяющей двум условиям:

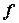— вычисляется полиномиальным алгоритмом;

— для всех 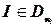, 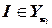тогда и только тогда, когда .

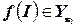Пример 5.1. Покажем сводимость задачи гамильтонов цикл (ГЦ) к задаче коммивояжера (ЗК).

Задача гамильтонов цикл заключается в следующем.

Условие. Задан неориентированный граф .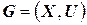

Вопрос. Верно ли, что 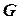содержит гамильтонов цикл (элементарный цикл, проходящий через все вершины графа)?

Рассмотрим индивидуальную ЗК, которая строится по конкретной индивидуальной задаче ГЦ: множество городов совпадает с множеством вершин, расстояние 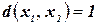, есл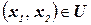и и 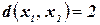, если 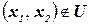. Границу 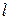для искомого маршрута положим равной 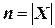. Построение индивидуальной задачи ЗК (обозначим ее через 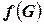) по существу сводится к вычислению 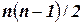расстояний, т. е. может быть осуществлено за полиномиальное от размерности индивидуальной задачи ГЦ (с параметром 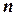) время.

Покажем, что G содержит гамильтонов цикл тогда и только тогда, когда в 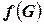имеется проходящий через все города маршрут длины, не превосходящей 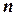. Пусть 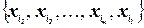‑ последовательность вершин графа, соответствующая гамильтонову циклу. Определим маршрут в 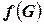той же последовательностью городов. Тогда длина этого маршрута, в соответствии с введенными расстояниями, равна 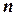, причем маршрут проходит через все города.

Определение 5.17. Язык 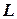называется -полным, если 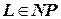, и для любого другого языка 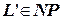следует, что 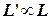(аналогично определяется -полная задача распознавания).

Теорема 5.3. Если 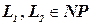, 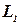‑ -полный язык, и 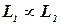, то 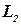также NP-полный язык.

Доказательство. Пусть 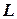‑ любой язык из класса . Тогда из 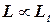и транзитивности отношения « 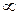» следует, что .

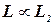Таким образом, для доказательства -полноты некоторой задачи распознавания достаточно показать, что некоторая известная -полная задача сводится к данной.

Теорема Кука

В соответствии с результатами, полученными в предыдущем параграфе, для исследования класса -полных задач необходимо получить хотя бы одну задачу, принадлежащую этому классу. В качестве такой задачи выступает известная задача выполнимости булевых формул (SAT).

Задача Выполнимость заключается в следующем.

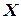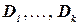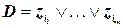Условие. Задано множество булевых переменных и набор дизъюнкций , где , a 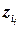‑ это либо 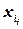либо ее отрицание .

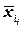Вопрос. Существует ли такой набор значений истинности на множестве X, что выполнима конъюнкция этих дизъюнкций 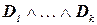?[3]

Теорема 5.4 (Кук). Задача Выполнимость ‑ - полная задача.

Схема доказательства.

1. Очевидно, что за полиномиальное число шагов можно убедиться в том, является или нет выполняющим конкретный набор значений истинности на 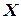для 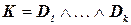. Выбор самого набора осуществляется недетерминированной процедурой. Таким образом, задача SAT лежит в классе .

2. Пусть задача SAT представлена некоторым языком 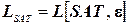для некоторой разумной схемы кодирования 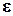. Для доказательства -полноты задачи SAT необходимо показать, что для всех языков 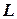из класса справедливо: 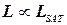. Учитывая то, что любой язык из может быть представлен в стандартном виде, а именно НДМТ-программой, распознающей этот язык, достаточно показать, что имеет место полиномиальная сводимость языка, распознаваемого этой программой, к .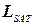

3. Формализуем процесс распознавания языка НДМТ-программой 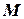, задаваемой компонентами 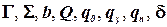и имеющей временную сложность 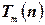, ограниченную сверху полиномом 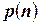. Условие 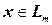равносильно одновременному выполнению шести условий, которые по сути задают работу машины Тьюринга:

1. В любой момент времени 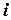(т. е. после 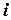шага, проверяющего вычисления) программа 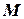находится ровно в одном состоянии;

2. В любой момент времени 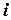читающая/пишущая головка просматривает ровно одну ячейку;

3. В любой момент времени 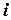каждая ячейка содержит ровно один символ из ;

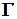4. В момент времени 0 вычисление находится в исходной конфигурации стадии проверки при входе .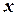

5. Не позднее, чем через 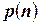шагов, 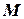переходит в состояние 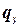и, следовательно, принимает .

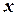6. Для любого момента времени 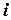, 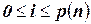конфигурация программы 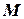в момент времени 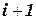получается из конфигурации в момент i одноразовым применением функции перехода .

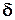Введем булевы переменные:

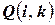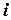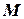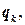
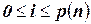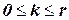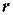‑ в момент времени программа находится в состоянии , , где ‑ число различных состояний, причем , .

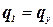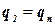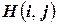‑ в момент времени 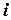читающая/пишущая головка просматривает ячейку с номером , .

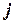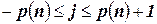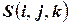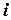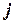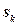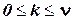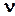‑ в момент времени в -й ячейке записан символ , , где ‑ число различных символов в алфавите 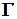, причем .

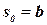4. Каждое из 6 сформулированных на этапе 3 условий может быть представлено в виде конъюнкции элементарных дизъюнкций введенных выше булевых переменных.

5. Анализ этих условий показывает, что для записи всех шести условий в общей сложности потребуется порядка 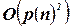элементарных дизъюнкций.

Длина каждой дизъюнкции не превосходит величины 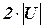, где 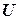‑ множество всех переменных, 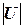ограничено .

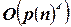Индивидуальная задача, записанная с помощью цепочки символов 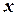( 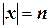), может быть преобразована в индивидуальную задачу SAT. Отсюда вытекает утверждение теоремы, что задача выполнимости SAT есть -полная задача.