Образование поверхностей многогранников

Образование любой поверхности можно представить как непрерывный ряд изображений, полученный при движении одной линии (образующей) по другой линии (направляющей). Поскольку и образующей и направляющей может быть произвольная кривая линия, то и поверхность может иметь любую произвольную форму, в общем случае достаточно сложную.

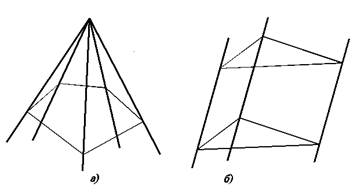
Рис. 5.1. Образование гранных поверхностей.

В том случае, когда образующая и направляющая являются прямыми линиями, получаем простейшую поверхность – плоскость. Если образующей является прямая линия, а направляющей ломаная, получаем гранную поверхность. Когда образующая закреплена в одной точке, при движении по направляющей она вычерчивает пирамидальную поверхность (рис. 5.1а). Если образующая перемещается параллельно какому-либо направлению, получаем призматическую поверхность (рис. 5.1б).

В дальнейшем из всех гранных поверхностей рассмотрим лишь призматическую и пирамидальную.

5.2. Точка и линия на поверхности многогранника

Рассмотрим задачу построения отсутствующих проекций точек 1, 2, 3, лежащих на поверхности прямой пирамиды (рис. 5.2).

Для определения положения горизонтальной проекции 1₁ используем образующую пирамиды: проведем через вершину S₂ и точку 1₂ прямую до пересечения с ребром А₂В₂ основания. Затем по линии связи получим горизонтальную проекцию этой точки на ребре А₁В₁. Соединив полученную точку с вершиной S₁, будем иметь горизонтальную проекцию образующей. На ней и лежит точка 1₁, положение которой определим по линии связи 1₂. Аналогично можно построить горизонтальную проекцию 2₁, с учетом того, что (2₂) – невидимая. Значит точка 2 лежит на грани SAC. Тогда основание образующей попадает на ребро АС основания. В остальном построения полностью повторяют предыдущие.

Однако для определения положения горизонтальной проекции 3₁ использовать образующую не представляется возможным, так как ребро SB, на котором лежит точка 3, в проекциях на П₁, П₂ дает вертикальную прямую (т.е. является профильной линией уровня). В этом случае используют линию, параллельную основанию. Через точку 3₂ проводят прямую, параллельную А₂В₂, до пересечения с ребром S₂A₂. Затем на ребре S₁A₁ по линии связи получают горизонтальную проекцию точки пересечения, через которую проводят прямую параллельно А₁В₁. Поскольку точка 3 лежит на этой прямой, то продолжая ее горизонтальную проекцию до пересечения с ребром S₁В₁, получаем точку 3₁.

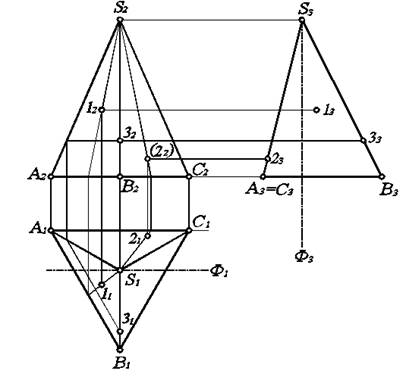
Рис. 5.2. Построение точек на поверхности пирамиды.

Профильную проекцию 1₃ строим на основании взаимосвязи между горизонтальной и профильной проекциями точки. А именно, откладываем по линии связи, проходящей через 1₂, от базовой линии Ф₃ вправо отрезок, равный расстоянию от 1₁ до Ф₁, как это делалось при построении профильной проекции пирамиды. Точка 2₃ лежит на пересечении горизонтальной линии связи, проходящей через 2₂, и грани S₃A₃C₃, превратившейся в прямую S₃A₃. Наконец, точку 3₃ находим на горизонтальной линии связи, проходящей через 3₂ и ребро S₃В₃.

Следует заметить, что горизонтальную проекцию 3₁ можно найти через профильную. Для этого измеряем расстояния от 3₃ до Ф₃ и откладываем его вниз от Ф₁ по ребру S₁В₁.

Линию на поверхности многогранника можно построить по характерным точкам, которыми являются точки ее изгиба и точки перехода через ребра. При этом следует помнить, что ломаная линия на поверхности многогранника будет ломаной, состоящей из отрезков прямой , в любой плоскости проекций, а кривая – кривой ( за исключением частных случаев).

5.3. Позиционные задачи

В этом разделе рассматриваются позиционные задачи на определение общих элементов многогранника и более простых по сравнению с ним геометрических объектов, таких как прямая и плоскость, а также способы построения линии пересечения многогранников между собой.

5.3.1. Пересечение многогранника прямой

Пусть требуется определить точки пересечения прямой а и призмы АВСА*В*С* (рис. 5.3).

Проведем через прямую а фронтально–проецирующую плоскость S. Тогда S₂=а₂. Определим фронтальные проекции точек пересечения плоскости S с прямой а. Это точки 1, 2, 3, 4, где плоскость S пересекает ребра призмы. Их фронтальные проекции 1₂, 2₂, 3₂, 4₂ легко получить на линии а₂. Ясно, что по этим точкам проходит фронтальная проекция 1₂2₂3₂4₂ плоской фигуры, полученной в результате пересечения S и призмы. Для построения ее горизонтальной проекции достаточно по линиям найти горизонтальные проекции 1₁, 2₁, 3₁, 4 точек, лежащих на соответствующих ребрах призмы, соединив которые получим искомую плоскую фигуру 1₁2₁3₁4₁. Стороны этого четырехугольника лежат на соответствующих гранях призмы.

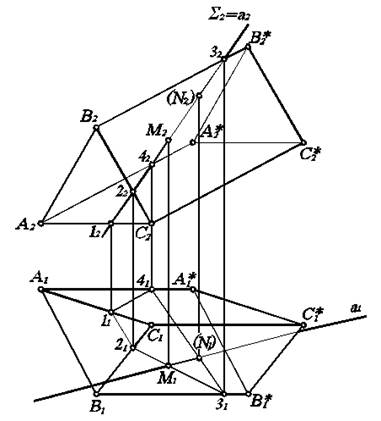
Рис. 5.3. Определение точек пересечения прямой и призмы.

Следовательно, зная видимость граней призмы, можно определить видимость сторон четырехугольника на П₁: невидимой является лишь сторона 3₁4₁. Одно, что точки М₁ и N₁- горизонтальные проекции точек пересечения прямой а и призмы, так как они одновременно принадлежат и прямой а и линиям 23 и 34, лежащим на поверхности призмы. По линиям связи найдем положение точек М₂ и N₂, лежащих на а₂.

Видимость определяется по принадлежности точек М и N граням призмы.

5.3.2. Натуральная величина сечения

Сечением многогранника называется плоская фигура, расположенная в секущей плоскости и ограниченная линиями пересечения ее с многогранником.

Часто приходится не только строить сечение многогранника плоскостью частного положения, но и определять натуральную величину сечения (рис 5.4). Пусть задана горизонтальная проекция S₁. Необходимо найти линию пересечения плоскости S с пирамидой и определить натуральную величину сечения. Таким образом, задача разбивается на две части: сначала надо построить сечение в плоскостях П₁и П₂, а затем определить его натуральную величину.

б)

а)

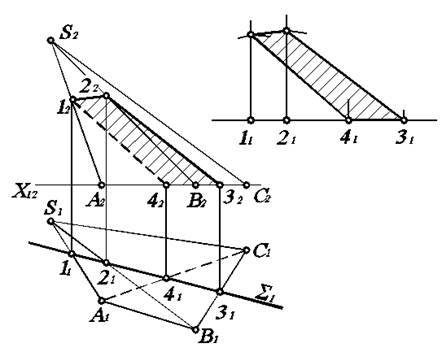
Рис. 5.4. Построение линии пересечения и определение натуральной величины сечения пирамиды плоскостью.

Найдем все точки пересечения плоскости S с ребрами пирамиды и соединим их отрезками прямой. Горизонтальная проекция S₁ пересекает ребра пирамиды в точках 1₁, 2₁, 3₁, 4₁ (рис. 5.4а). По линиям связи находим их фронтальные проекции 1₂, 2₂, 3₂, 4₂ на фронтальных проекциях соответствующих ребер. Соединяя найденные точки, получаем линию пересечения 1₂2₂3₂4₂ заданной плоскости с пирамидой. Плоская фигура, ограниченная полученной линией (на рис. 5.4а заштрихована), и является сечением пирамиды плоскостью. В нашем примере это четырехугольник 1234.

Для определения натуральной величины четырехугольника 1234 способом замены плоскостей проекций не обязательно строить новую ось параллельно S₁ (или 1₁2₁4₁3₁), ввиду ограниченности площади чертежа. Достаточно соблюдать основные принципы построения. Начертим новую ось на свободном поле чертежа. Перенесем на нее точки 1₁,2₁,4₁,3₁, не меняя расстояния между ними. Проведем через них перпендикуляры к оси. Затем отложим на построенных перпендикулярах отрезки, равные расстояниям от оси П₂/П₁, которую считаем расположенной на основании А₂В₂С₂ пирамиды, до соответствующих проекций 1₂, 2₂, 4₂, 3₂. Соединив указанные точки, получим натуральную величину сечения пирамиды заданной плоскостью S (рис. 5.4б).

5.3.3. Пересечение двух многогранников

При пересечении двух многогранников общим геометрическим элементом является замкнутая ломаная линия, состоящая из участков прямой. Точки излома получаются в местах пересечения граней одного многогранника с ребрами другого.

В том случае, когда один из многогранников занимает частное положение (т.е. его боковые грани проецируются на одну из плоскостей проекций в многоугольник), задача построения линии их пересечения решается достаточно просто. Ввиду того, что одна из проекций многогранника – многоугольник, проекция линии пересечения на эту плоскость проекций совпадает с ним. Поскольку линия пересечения многогранников принадлежит каждому из них, то задача сводится к построению отсутствующих проекций ломаной линии, а следовательно, к построению проекций точек на поверхности многогранника. Пусть пересекаются пирамида и призма частного положения (рис. 5.5). Требуется построить проекции линии их пересечения.

Поскольку призма расположена так, что все ее боковые грани перпендикулярны П₁, то на П₁ ее боковая поверхность проецируется в треугольник D₁E₁F₁. И горизонтальной проекцией линии пересечения призмы DEFD*E*F* и пирамиды SABC является ломаная линия 1₁Е₁5₁. Таким образом, горизонтальная проекция линии пересечения призмы и пирамиды получена без каких бы то ни было дополнительных построений. Следует учитывать, что грани призмы пересекают не только грань SAC, но и грани SBC и SAB пирамиды. Следовательно, можно отметить все точки излома линии пересечения 1₁Е₁5₁, расположенные на пересечении ее с ребрами пирамиды. А именно, точки 1₁, 2₁, 3₁, 4₁, 5₁, 6₁. Очевидно, что 3₁=6₁, так как ребро ЕЕ* призмы пересекает две грани SAB и SAС пирамиды.

Линия пересечения на каждой из проекций должна быть замкнутой. Причем ясно, что можно соединять отрезками прямой лишь точки, лежащие на одной и той же грани. Эти правила универсальны, и относятся к любой задаче о пересечении многогранников.

Тогда на П₁ получаем горизонтальную проекцию линии пересечения призмы и пирамиды в виде ломаной 1₁2₁3₁4₁5₁6₁1₁, лежащей на гранях пирамиды (вместе с тем и призмы).

Для нахождения фронтальной проекции этой линии необходимо решить задачу построения проекций ломаной линии на поверхность пирамиды. Достаточно построить фронтальные проекции указанных точек. Так как точки 1, 2, 4, 5 лежат на ребрах пирамиды, то их фронтальные проекции 1₂, 2₂, 4₂, 5₂ легко получить по линиям связи. Для нахождения фронтальных проекций 3₂ и 6₂ точек 3 и 6, лежащих на гранях SAB и SAС соответственно, необходимо через точки 3₁ и 6₁ провести образующие S₁7₁ и S₁8₁. Точки 7 и 8 лежат на основании пирамиды, поэтому по линиям связи можно найти фронтальные проекции 7₂ и 8₂ на соответствующих ребрах основания А₂С₂ и А₂В₂ пирамиды. Построив фронтальные проекции S₂7₂ и S₂8₂ образующих, по линиям связи отметим на них точки 3₂ и 6₂. Соединив точки, получим замкнутую ломаную 1₂2₂3₂4₂5₂6₂1₂. Последовательность соединения определяется по горизонтальной проекции на основании правила принадлежности соседних точек пересечения одной и той же грани.

Видимость точек и линий на П₂ определяется по принадлежности граням пирамиды.

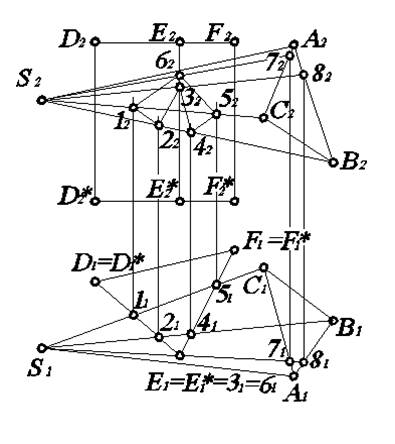
Рис. 5.5. Построение линии пересечения пирамиды и призмы частного положения.

5.4. Развертка многогранника

Разверткой многогранника называется плоская фигура составленная из его граней, развернутых на одну плоскость.

5.4.1. Развертка призмы. Методы нормального сечения и раскатки.

Для развертки призмы применяют два метода: нормального сечения и раскатки. Рассмотрим последовательно каждый из них.

А. Метод нормального сечения.

Пусть требуется построить развертку наклонной трехгранной призмы АВCDEF (рис. 5.6).

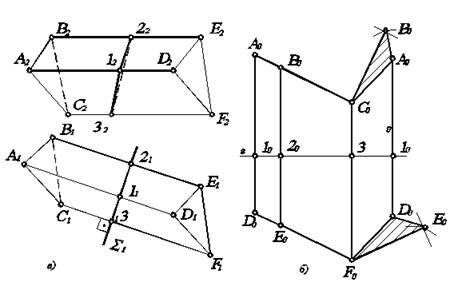
Рис. 5.6. Развертка наклонной трехгранной призмы.

Пересечем призму АВCDEF плоскостью S₁, перпендикулярной к боковым ребрам призмы. Построим сечение заданной призмы этой плоскостью – треугольник 123. Определим длины сторон треугольника 123. В свободном поле чертежа проведем прямую линию а (на рис. 5.6 прямая линия проведена горизонтально). От произвольной точки 1₀, взятой на этой прямой, отложим отрезки 1₀2₀, 2₀3₀, 3₀1₀, равные сторонам треугольника 123. Через точки 1₀, 2₀, 3₀, 1₀ проведем прямые, перпендикулярные прямой а, и отложим от точек 1₀, 2₀, 3₀, 1₀ отрезки, равные соответствующим длинам боковых ребер (1А, 1D, 2В, 2Е,…). Полученные точки А₀, В₀, C₀, A₀ и D₀, E₀, F₀, D₀ соединяем прямыми. Плоская фигура А₀В₀C₀A₀D₀F₀E₀D₀ представляет собой развертку боковой поверхности призмы.

Чтобы получить полную развертку призмы, необходимо к развертке боковой поверхности пристроить основание призмы – треугольники АВС и DЕК, предварительно определив их неискаженные размеры.

5.4.2. Развертка пирамиды методом треугольников (триангуляции)

Для развертки боковой поверхности пирамиды применяют метод треугольников (триангуляции), который заключается в построении последовательно каждой боковой грани пирамиды, представляющей собой треугольник.

Пусть требуется сделать развертку четырехгранной пирамиды SABCD (рис. 5.7а

Сначала определим натуральную величину каждого из боковых ребер. Удобнее использовать способ вращения вокруг проецирующей оси. За ось i выбираем горизонтально–проецирующую прямую, проходящую через вершину S пирамиды. Вращаем проекции точек А₁, В₁, С₁, D₁ вокруг S₁ до совмещения с горизонтальной прямой, проходящей через S₁. Тогда горизонтальные проекции боковых ребер пирамиды примут новое положение S₁A₁*, S₁B₁*, S₁C₁*, S₁D₁*, параллельно горизонтальной оси проекций, т.е. ребра SA, SB, SC, SD будут приведены в положение фронталей. Остается получить фронтальные проекции боковых ребер в новом положении, после вращения. В соответствии со способом вращения вокруг проецирующей оси, в то время, когда одна из проекций точки вращается вокруг оси, другая перемещается по горизонтальной линии. На горизонтальных линиях, проходящих через точки А₂, В₂, С₂, D₂, находим их новое положение А₂*,В₂*,С₂*,D₂* по линиям связи с А₁*,В₁*,С₁*,D₁* соответственно. Тогда отрезки S₂A₂*, S₂B₂*, S₂C₂*, S₂D₂* и являются натуральными величинами каждого из боковых ребер.

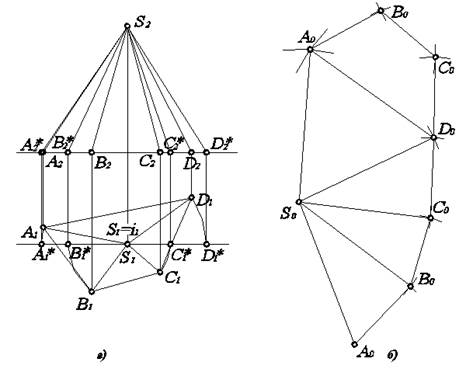
Рис. 5.7. Развертка пирамиды.

Таким образом, предварительные построения закончены, теперь вычертим развертку боковой поверхности пирамиды. Для этого необходимо знать натуральную величину ребер основания пирамиды. В данном случае не требуется никаких дополнительных построений, так как основание пирамиды – четырехугольник АВСD – занимает положение горизонтальной плоскости уровня. Следовательно, длина проекций A₁B₁, B₁C₁, C₁D₁, D₁A₁ является натуральной величиной соответствующих ребер.

Построение развертки боковой поверхности сводится к построению треугольника по трем сторонам.

В случае, когда основание пирамиды занимает общее положение в пространстве, необходимо либо определить его натуральную величину способом замены плоскостей проекций, либо способом вращения вокруг проецирующей оси найти натуральную величину каждого ребра основания.

Кривые поверхности

В начертательной геометрии поверхность рассматривается как множество последовательных положений некоторой линии – образующей поверхности, перемещающейся в пространстве определенным образом по другой линии, которую называют направляющей.

Образующая поверхности в процессе движения может изменять свою форму. Одна и та же поверхность может быть образована перемещением различных линий.

Поверхности можно разбить на классы:

1) линейчатые поверхности;

2) винтовые поверхности;

3) циклические поверхности;

4) поверхности вращения.

Наибольшее распространение в технике получили поверхности вращения.

6.1. Поверхности вращения

Поверхности вращения образуются при вращении некоторой произвольной линии вокруг оси. В этом случае образующей является указанная линия, а направляющей - окружность. Форма поверхности вращения определяется формой образующей.

Пусть произвольная линия AGEB вращается вокруг оси i. Тогда она образует поверхность вращения (рис. 6.1).

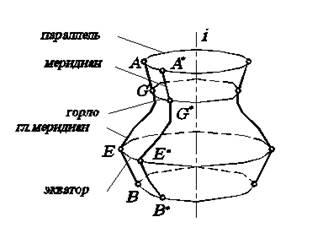
Рис. 6.1. Образование поверхности вращения.

Линия пересечения поверхности вращения плоскостью, проходящей через ось i, называется меридианом (например A*G*E*B*). Меридиан, лежащий в плоскости, параллельной П₂, называется главным. Линия пересечения поверхности вращения плоскостью, перпендикулярной оси i, называется параллелью. Таковыми являются направляющие, проходящие через точки АА*, ВВ*, ЕЕ*, GG*. Параллель, проходящая через наиболее удаленную от оси точку Е образующей, называется экватором, а через самую близкую точку G – горлом. Очевидно, что все параллели представляют собой окружности.

Одной из самых простых поверхностей вращения является цилиндр. Цилиндрическая поверхность образуется при вращении прямой (образующей) АВ вокруг оси (рис. 6.2а).

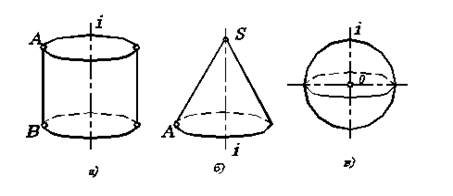
Рис. 6.2. Образование поверхности цилиндра, конуса, сферы.

В случае образования конической поверхности прямая AS, вращающаяся вокруг оси, закреплена в некоторой точке S на оси (рис. 6.2б). Такая поверхность подобна пирамидальной, у которой образующей является тоже прямая, но перемещающаяся по ломаной линии. Для того, чтобы получить цилиндр или конус, надо соответствующую поверхность ограничить плоскостями основания.

Если в качестве образующей выбираем окружность, то при ее вращении вокруг оси получаем:

- сферу, когда ось вращения проходит через центр О окружности (рис. 6.2в);

- тор, в противном случае (рис. 6.3).

Если ось вращения проходит через образующую–окружность, тор получается закрытым (рис. 6.3а), в противном случае-открытым (рис. 6.3б). Примером открытого тора может служить бублик, закрытого – яблоко.

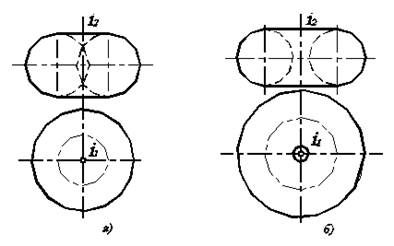
Рис. 6.3. Образование поверхности тора.

6.2. Точка и линия на поверхностях вращения

Рассмотрим в качестве примера построение точки и линии на некоторых поверхностях вращения.

6.2.1. Конус

Построить отсутствующие проекции точек А и В, расположенных на поверхности прямого кругового конуса, если известно положение А₂ и В₂ (рис.6.4).

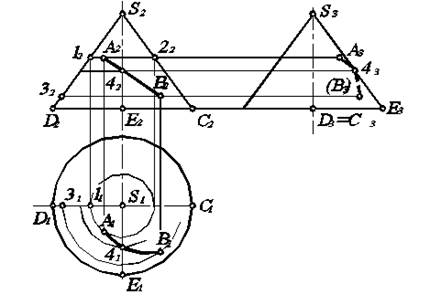
Рис. 6.4. Построение проекций точек и линии на поверхности конуса.

Для построение горизонтальной проекции точки, например А, необходимо через ее фронтальную проекцию провести горизонтальную линию. Тогда на П₁ эта линия 12 представляет собой дугу окружности диаметром 1₂2₂=1₁2₁. По линии связи на ней находим А₁. Аналогично, проводя дугу окружности радиусом S₁3₁, равным расстоянию от оси конуса до точки 3₂ на его контуре, определяем положение на ней точки В₁. По этим проекциям находим положение А₃, В₃.

В. По известной проекции А₂В₂ линии на поверхности конуса построить горизонтальную и профильную.

Выбрав на линии А₂В₂ промежуточную точку 4₂, найдем 4₁ так же, как сделали это для точек А и В. Соединив точки А₁, 4₁, В₁, получим горизонтальную проекцию линии АВ.

Для построения профильной проекции А₃В₃ необходимо найти положение контурной точки 4, лежащей на SA. По фронтальной проекции 4₂, лежащей на S₂A₂, находим профильную проекцию 4₃, лежащую на S₃A₃. Теперь точки А₃, 4₃, В₃ можно соединить линией.

При соединении точек линией всегда надо руководствоваться достаточно очевидным правилом: на каждой проекции точки, принадлежащие линии, следует соединять в одинаковой последовательности. Так, если на фронтальной проекции точка 4 является промежуточной, то она будет промежуточной и на других проекциях.

6.2.2. Сфера

Проекцией сферы на любую плоскость проекций является окружность.

А. Рассмотрим построение проекций точек на поверхности сферы (рис. 6.5). Точки, лежащие на экваторе, обозначим через А, В, С, D; точки, лежащие на главном меридиане – А, Е, С, F. Очевидно, что точки А и С принадлежат одновременно и экватору, и главному меридиану.

При построении проекций следует иметь ввиду, что любая параллель на П₂ проецируется в горизонтальную прямую, а на П₁ в окружность.

Пусть задана фронтальная проекция точки М. Проведем через нее параллель. Тогда на П₂ получим горизонтальную прямую, проходящую через точку М₂. А на П₁ – дугу окрудности радиусом F₁1₁, равным расстоянию от вертикальной оси до токи 1₂. Ясно, что точка М₁ лежит на этой окружности. По двум проекциям М₁ и М₂, используя правило взаимосвязи проекций, построим М₃.

Видимость и невидимость полушарий, а следовательно, и точек, лежащих на них, можно легко определить, рассматривая с разных точек зрения обыкновенный резиновый мячик, нарисовав на нем экватор и два меридиана, расположенных в плоскостях, перпендикулярных друг другу.

В. Построим горизонтальную и профильную проекции линии МN, если известна ее фронтальная проекция М₂N₂, состоящую из прямолинейных отрезков М₂3₂ и 3₂N₂.

Очевидно, что точка 3₁ лежит на А₁Е₁, так как 3₂ - на А₂Е₂. При этом прямая МN проходит через экватор (точка 4₂). Следовательно, на П₁ – через точку 4₁. А участок 4₁3₁ – невидимый, поскольку, как видно по его фронтальной проекции 4₂3₂, он лежит в нижнем полушарии, т.е. ниже экватора.

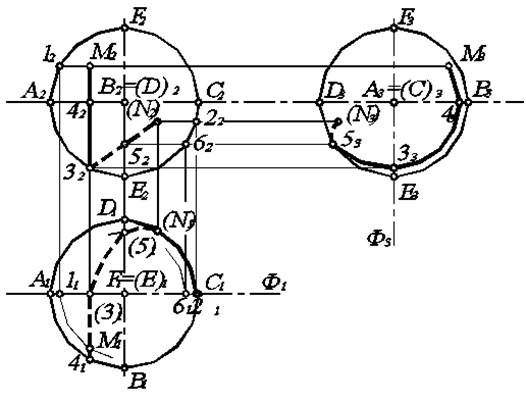
Рис. 6.5. Построение проекций точек и линии на поверхности сферы.

Для построения проекций участка 3N выберем промежуточную точку 5₂. Тогда точка 5₁ лежит на дуге окружности радиуса 5₂6₂. Соединив точки 3₁, 5₁, N₁, получим искомую линию М₁4₁3₁5₁N₁.

Построим профильную проекцию М₃N₃, которая проходит через те же промежуточные точки. Так как М₂3₂ – вертикальная прямая, то на П₃ она представляет собой дугу М₃3₃ окружности радиуса 4₂3₂=А₃3₃. Точка 5₃ – контурная для профильной проекции сферы. Значит, остается соединить точки 3₃, 5₃, N₃ кривой линией. При этом участок 5₃N₃ – невидимый.

Если в нашу задачу входит более точное построение проекций линии MN, тогда на всех участках, где ее проекции не являются отрезками прямой или окружности, необходимо выбрать несколько промежуточных точек.

6.3. Пересечение поверхности вращения и многогранника

При пересечении поверхности вращения многогранником их общим геометрическим элементом является некоторая линия.

Рассмотрим построение этой линии на примере решения задачи о пересечении прямой трехгранной призмы и сферы (рис. 6.6).

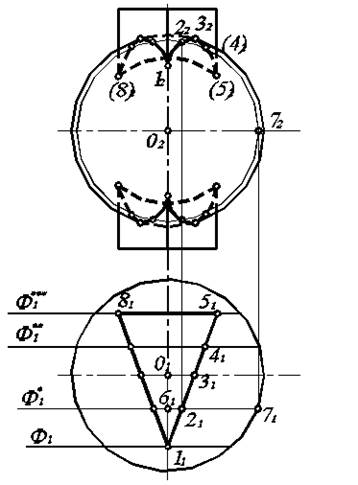
Рис. 6.6. Пересечение призмы и сферы.

Поскольку боковые грани призмы перпендикулярны к П₁, то горизонтальная проекция линии пересечения призмы и сферы совпадает с горизонтальной проекцией призмы.

Остается построить фронтальную проекцию линии пересечения. Применим метод вспомогательных секущих плоскостей, в качестве которых выберем фронтальные плоскости уровня, проходящие через характерные (1, 3, 5) и промежуточные (2, 4) точки, лежащие на линии пересечения призмы и сферы. Их горизонтальные проекции 1₁, 2₁, 3₁, 4₁, 5₁ указаны на рис. 6.6.

Линией пересечения фронтальной плоскости уровня со сферой является окружность, для построения которой на П₂ достаточно измерить расстояние от вертикальной оси до контура сферы на П_1, а затем этим радиусом на П₂ провести окружность.

Рассмотрим построение фронтальной проекции какой-либо точки, например, точки 2. Проводим через нее фронтальную плоскость Ф*. Затем измеряем расстояние от точки 6₁ до 7₁ и этим радиусом проводим дугу окружности из точки О₂. Искомая точка лежит на пересечении этой дуги с линией связи, проведенной из точки 2₁. Аналогично строятся точки 1₂, 4₂, 5₂. Точка 3 лежит на контуре сферы в проекции на П₂, и для построения точки 3₂ достаточно провести из точки 3₁ линию связи до пересечения ее с контуром сферы.

Соединив точки 1₂, 2₂, 3₂, 4₂, 5₂, получаем один из участков искомой линии.

Так как участок линии между точками 5 и 8 лежит на фронтальной плоскости Ф***, что видно на его горизонтальной проекции 5₁8₁, то между точками 5₂ и 8₂ линия пересечения призмы и сферы представляет собой дугу окружности, проведенной через точку 5₂.

В связи с тем, что рассматриваемые поверхности симметричны относительно горизонтальной и профильной плоскостей уровня, искомая линия пересечения в проекции на П₂ симметрична относительно вертикальной и горизонтальной осей, и ее построение не требует дополнительных пояснений.

Используя метод вспомогательных секущих плоскостей, можно построить линию пересечения любых поверхностей вращения и многогранников.

6.4. Пересечение поверхностей вращения. Метод вспомогательных секущих концентрических сфер

Оговоримся, что этот метод применим лишь в случае выполнения трех условий:

1. Обе поверхности, линию пересечения которых мы определяем, являются поверхностями вращения;

2. Их оси должны пересекаться;

3. Оси этих поверхностей вращения должны быть параллельны одной из плоскостей проекций.

Решим задачу о пересечении двух конусов, оси которых пересекаются и параллельны П₂ (рис. 6.7).

Центром концентрических сфер, которые обеспечивают дополнительные построения, необходимые для решения задачи, является точка пересечения осей поверхностей вращения. В данном случае это точка О пересечения осей конусов.

Рассмотрим построение точек пересечения конусов с помощью произвольной сферы (рис. 6.7). Ее проекция на П₂ представляет собой окружность такого же радиуса, как и сфера.

А проекцией на П₂ линии пересечения построенной секущей сферы с конусом является прямая, параллельная основанию конуса. Ее можно построить, соединив точки пересечения окружности и контура конуса. Очевидно, что таких прямых две для каждого конуса.

Точки А₂, В₂, С₂ пересечения этих прямых между собой и являются фронтальными проекциями точек пересечения конусов. Как видим, используя только одну окружность, можно получить несколько точек пересечения конусов. Ясно, что их не может быть более четырех для одной дополнительно построенной сферы.

Далее не составляет труда построить горизонтальные проекции точек А, В, С, учитывая, что каждая из них является точкой на поверхности прямого конуса. Как излагалось ранее, для этого достаточно измерить расстояния от оси конуса до его контура по прямой, проходящей через точку, горизонтальную проекцию которой строим. Затем этим радиусом из точки О₁ провести окружность и на ней по линии связи найти горизонтальную проекцию. На рис. 6.7 указанные построения выполнены для точки С. Поскольку ей на П₁ соответствует две точки С₁ и С₁*, то понятно, что на П₂ имеем дело с двумя конкурирующими точками. Поэтому, уточняя предыдущие замечания, следует отметить, что построенная секущая сфера дает не три, а шесть точек пересечения конусов. Построение горизонтальных проекций остальных точек ничем не отличается от вышеприведенного.

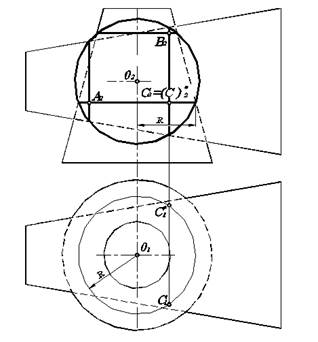
Рис. 6.7. Построение точек пересечения конусов.

Для того, чтобы построить линию пересечения конусов, точек, через которые она проходит, должно быть достаточное количество. Дальнейшее решение поставленной задачи рассмотрим на рис. 6.8. Четыре точки 1₂, 2₂, 3₂, 4₂ имеем без дополнительных построений, так как они лежат на пересечении образующих конусов. Остальные точки на П₂ получим, проведя четыре окружности. Для окружности радиуса R₁ фронтальными проекциями точек пересечения конусов являются 5₂, 5₂*, 5₂**, 5₂***. Для окружности радиуса R₂ таких точек две – 6₂, 6₂*. Окружность радиуса R₃ дает также две точки - 7₂, 7₂*. Окружность радиуса R₄ позволяет получить лишь одну точку 8₂. Очевидно, что проводить окружности радиусом, большим чем О₂4₂, и меньшим, чем R₂, не имеет смысла, так как не получим ни одной точки пересечения.

Как видно на рис. 6.8, четырех окружностей достаточно для того, чтобы построить фронтальную проекцию линии пересечения конусов, соединив найденные точки.

Для построения горизонтальной проекции полученных точек необходимо решить рассмотренную ранее задачу построения точек на поверхности конуса. Так, для построения точки, например, 7₁ надо измерить расстояние по горизонтальной линии, проходящей через 7₂, от оси до контура конуса, а затем этим радиусом из точки О₁ провести дугу. Точка 7₁ лежит на пересечении этой дуги с линией связи, проведенной из 7₂. Аналогично строятся горизонтальные проекции остальных точек.

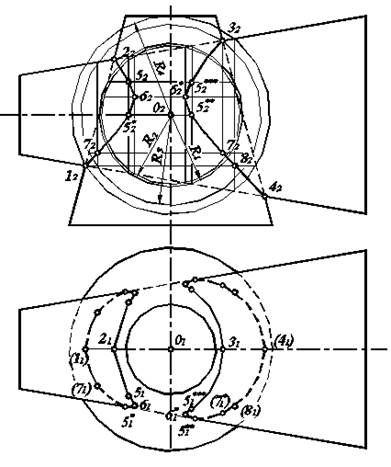
Рис. 6.8. Пересечение двух конических поверхностей.

Поскольку точки 5* и 5** лежат на образующей горизонтального конуса, которая на П₁ является контурной, то, очевидно, что точки 5₁* и 5₁** служат точками перехода линии пересечения конусов из видимой зоны в невидимую.

С учетом того, что изображенные поверхности симметричны относительно фронтальной плоскости уровня, соединив построенные точки кривой линией, получим решение в окончательном виде (рис. 6.8).

6.5. Развертка цилиндра и конуса

Из всех поверхностей построение развертки возможно лишь для линейчатых поверхностей, образующей которых является прямая. К таковым относятся две – цилиндр и конус – из рассматриваемых нами поверхностей вращения. Развертку сферы и тора построить нельзя.

Построение развертки цилиндра и конуса осуществляется в одинаковой последовательности. Сначала раскатываем боковую поверхность, а затем пристраиваем основание.

Рассмотрим построение развертки прямого цилиндра. (рис. 6.9).

Развертка боковой поверхности прямого цилиндра представляет собой прямоугольник, высота которого Н равна длине образующей А₂А₂*, изображенной на П₂, а ширина – длине окружности 2pR, где R – радиус основания конуса, заданного без искажений на П_1. Остается дополнить чертеж разверткой основания, которая полностью совпадает с его горизонтальной проекцией. При этом точка К касания основания выбирается произвольно на длинной стороне полученного прямоугольника.

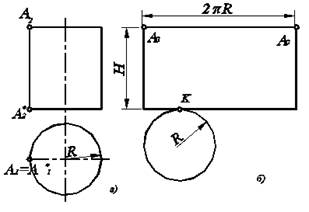
Рис. 6.9. Развертка прямого цилиндра: а) комплексный чертеж, б) развертка цилиндра.

Построим развертку прямого конуса (рис. 6.10). Боковая поверхность разворачивается в сектор окружности радиуса S₀A₀, равного длине образующей конуса. В данном примере длина образующей конуса L=S₀A₀=S₂A₂, так как SА параллельна П₂. Центральный угол сектора вычисляется по формуле:

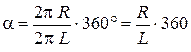
В рассматриваемом примере 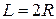, поэтому 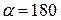°. Тогда развертка боковой поверхности представляет собой половину круга радиуса L. Чтобы получить полную развертку прямого конуса, нужно достроить основание, равное площади круга радиуса R. Причем таким образом, чтобы этот круг касался развертки боковой поверхности в некоторой точке К.

Задача усложняется, когда необходимо построить развертку, например, наклонного конуса, расположенного по отношению к плоскостям проекций произвольным образом.

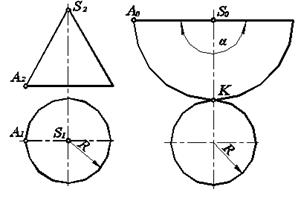
Рис. 6.10. Развертка прямого конуса: а) комплексный чертеж конуса, б) развертка конуса.