Структура и методы декомпозиции задач удовлетворения ограничений

В данном разделе рассматриваются способы, позволяющие использо­вать для быстрого поиска решений структуру самой задачи, представленную в виде графа ограничений. Большинство описанных здесь подходов является очень общими и применимыми для решения других дискретных задач, помимо УО.

Графовые методы

Графовые методы используют структуру графа ограничений при реше­нии задачи УО.

Ниже рассмотрены 3 графовых метода, которые используют то, что задача УО с древовидным графом ог­раничений может быть решена за линейное время, причем древовидная структура находится или строится из заданной задачи УО.

Для разбиения задачи УО на независимые подзадачи, можно рассмот­реть связные компоненты графа ограничений. Каждый компонент соответст­вует одной подзадаче УО . Если присваивание является решением УО , то 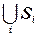является решением 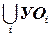. Почему это так важно? Рассмотрим следую­щее: предположим, что каждая подзадача УО имеет 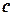переменных из об­щего количества 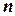переменных, где 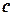‑ константа. В таком случае должно быть 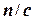подзадач, и для решения каждой из них требуется, самое большее, объем работы 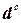. Поэтому общий объем работы измеряется величиной 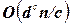, которая линейно зависит от 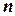; без такой декомпозиции общий объем работы измерялся бы величиной 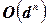, которая экспоненциально зави­сит от 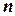. Приведем более конкретный пример: декомпозиция булевой задачи УО с 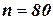на четыре независимые подзадачи с 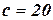сокращает продолжи­тельность поиска решения в наихудшем случае от величины, равной времени существования всей Вселенной, до величины, меньшей одной секунды. По­этому полностью независимые подзадачи являются привлекательными, но встречаются редко. В большинстве случаев подзадачи любой задачи УО свя­заны друг с другом. Простейшим случаем является тот, в котором граф огра­ничений образует дерево: любые две переменные связаны не больше чем од­ним путем.

Ниже будет показано, что любая задача УО с древовидной структурой может быть решена за время, линейно зависящее от количества переменных. Этот алгоритм имеет перечисленные ниже этапы.

· Выбрать в качестве корня дерева любую переменную и упорядо­чить переменные от корня до листьев таким образом, чтобы родительская вершина каждой вершины в дереве предшествовала этой вершине в таком упорядочении. Обозначить эти переменные по порядку как 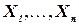. Теперь каждая переменная, кроме корня, имеет только одну родительскую перемен­ную.

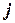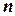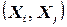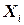· В цикле по от до 2 применять проверку совместимости к ду­гам , где ‑ родительская вершина вершины 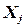, удаляя значения из области определения 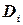по мере необходимости.

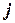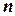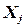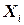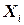· В цикле по от 1 до присваивать любое значение, совмести­мое со значением, присвоенным , где ‑ родительская вершина вершины .

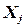Теперь, после создания эффективного алгоритма для деревьев, следует рассмотреть вопрос о том, можно ли каким-то образом приводить к древо­видным структурам более общие графы ограничений. Существуют два ос­новных способа выполнения этой задачи; один из них основан на удалении вершин, а другой ‑ на слиянии вершин друг с другом и образовании супер-вершин. Первый подход предусматривает присваивание значений некоторым переменным так, чтобы оставшиеся переменные образовывали дерево.