Химический потенциал

До сих пор мы рассматривали закрытые системы, в которых количество вещества оставалось неизменным. Формулы таблицы 16.1 справедливы именно для такого случая. Между тем достаточно часто возникает необходимость рассматривать системы с переменным числом частиц. Примером могут служить тела, в которых происходят те или иные химические превращения, или системы, в которых происходят фазовые превращения (испарение, плавление и т.п.)

Если система обменивается веществом со своим окружением, то изменение числа частиц в системе сопровождается изменением энергии. Это означает, что в соотношении (16.2) внутреннюю энергию следует рассматривать как функцию трех переменных U = U(S,V,n). Тогда в выражение (16.1) для дифференциала внутренней энергии следует добавить слагаемое, пропорциональное изменению количества вещества, которое будем характеризовать числом молей n

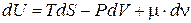, (20.1)

где коэффициент пропорциональности m имеет размерность энергии на моль и называется химическим потенциалом вещества. Такие же слагаемые войдут в дифференциалы других термодинамических функций:

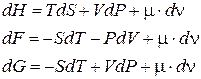. (20.2)

Из выражений (20.1-2) следует, что

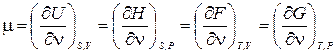. (20.3)

Напомним, что все термодинамические величины можно разделить на интенсивные и экстенсивные (см. § 2). Интенсивные величины зависят только от внутреннего состояния тел, но не от их размеров. К ним относятся, например, температура и давление. Значения экстенсивных величин для систем, состоящих из одинаковых частиц, изменяются пропорционально количеству вещества в системе, если при этом ее внутреннее состояние не меняется. Примером являются объем, внутренняя энергия, энтропия и т.п. При делении экстенсивной величины на число молей получается интенсивная величина. Например, объем одного моля вещества (молярный объем) 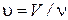, молярная энтропия 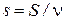. Все термодинамические функции являются экстенсивными величинами. Их можно представить в виде

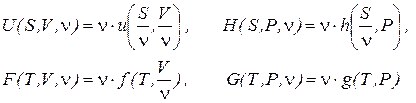(20.4)

где u, h, f и g термодинамические функции одного моля вещества.

Из соотношений (20.3-4) видно, что химический потенциал mнаиболее просто связан с термодинамическим потенциалом G, аргументами которого, кроме числа молей n, являются только интенсивные переменные Т и Р.

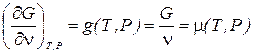. (20.5)

Таким образом, химический потенциал m = m(Т,Р) есть термодинамический потенциал G, отнесенный к одному молю вещества. Вследствие этого дифференциал химического потенциала

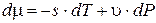. (20.6)

Химический потенциал является интенсивной величиной. В большинстве случаев формула, выражающая зависимость m = m(Т,Р) неизвестна, но можно получить представление о характере этой зависимости пользуясь производными химического потенциала

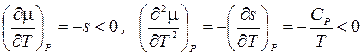, (20.7)

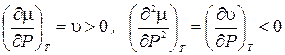. (20.8)

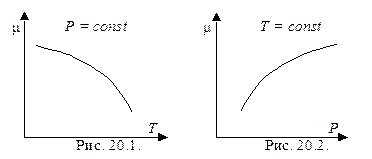На рис. 20.1 показана зависимость химического потенциала от температуры при постоянном давлении, а на рис. 20.2 – от давления при постоянной температуре.

Уменьшение m с ростом температуры при постоянстве давления можно объяснить с помощью соотношений (20.8). Молярная энтропия s всегда положительна, так что производная 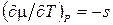всегда отрицательна. Вторая производная 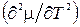тоже отрицательна, поэтому график зависимости m(Т) (рис.20.1) всегда выпуклый.

Если температура поддерживается постоянной, то из соотношений (20.8) следует, что химический потенциал растет с ростом давления (рис. 20.2), причем график m(Р) выпуклый.