Принципы оптимизации и моделирования при проектировании автомобильных дорог

Развитие вычислительной техники и технических средств автоматизации предопределило не только фундаментальное переосмысление и видоизменение технологии проектно-изыскательских работ, но и методов проектирования. В частности, широкое распространение в практике проектирования автомобильных дорог получили методы оптимизации [1,2,3,4,5,6] и моделирования [6,7], применение которых определяет заметное снижение материалоемкости и стоимости строительства и резкое повышение качества проектируемых объектов.

Реализация методов оптимизации и математического моделирования в связи с их исключительной многодельностью немыслима при ручной традиционной технологии и именно в связи с этим эти методы до недавнего времени не находили применения при проектировании автомобильных дорог.

Бурное развитие прикладной математики, связанное с научно-технической революцией, и широкое внедрение компьютерной техники в практику проектирования определили процесс изменения методов решения основных задач проектирования автомобильных дорог: плана трассы, продольного профиля, земляного полотна, дорожных одежд, малых водопропускных сооружений, мостовых переходов, системы поверхностного и подземного дорожного водоотвода, транспортных развязок движения, оценки проектных решений.

Основная задача теории оптимизации сводится к отысканию экстремума (минимума или максимума) скалярной функции f(х)п - мерного векторного аргумента X при заданном комплексе ограничений. Эту задачу представляют следующим образом:

min f(х),

x Î X, где (25.1)

X - некоторое множество n-мерного Евклидова пространства.

Функцию f(х) принято называть целевой функцией или функцией цели.

Точка 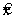определяет глобальный минимум функции цели f(x) на множестве X, если 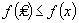для всех значений x Î X (рис. 25.2).

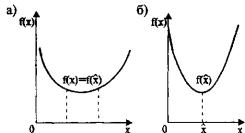
Рис. 25.2. Глобальный оптимум функции f(x):
а - в пределах интервала; б - в точке

Точка 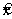определяет локальный минимум функции цели f(x) на множестве X, если при некотором достаточно малом e > 0 для всех 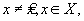удовлетворяющих условию 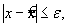выполняется неравенство 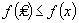(рис. 25.3).

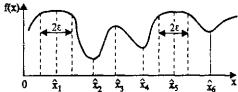
Рис. 25.3. Локальный оптимум функции f(x)

Как следует из рис. 25.3, точка 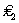определяет глобальный минимум, в то время как точка 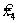- локальный.

Применительно к решению задач проектирования автомобильных дорог функция цели (объемы работ, строительная стоимость, дисконтные затраты и т.д.) является функцией многих переменных, т.е. целевым функционалом и поиск его экстремумов методами классического анализа в подавляющем большинстве случаев невозможен. В связи с этим в практике проектирования автомобильных дорог стали применять многочисленные специальные математические методы оптимизации, в частности:

методы оптимизации, основанные на решении задач линейного программирования и позволяющие определять экстремумы линейных функций при заданном комплексе ограничений;

методы оптимизации, основанные на решении задач нелинейного программирования и позволяющие определять экстремумы нелинейных при заданном комплексе ограничений;

эвристические методы, дающие возможность за приемлемое машинное время находить проектные решения, приближающиеся к оптимальным.

В настоящее время при автоматизированном проектировании автомобильных дорог с использованием оптимизационных алгоритмов решают главным образом следующие задачи:

проектирование сетей автомобильных дорог;

проектирование плана автомобильных дорог;

проектирование продольного профиля;

проектирование земляного полотна;

проектирование пойменных насыпей на подходах к мостам;

проектирование дорожных одежд;

проектирование водопропускных труб;

проектирование системы поверхностного дорожного водоотвода;

проектирование мостов и путепроводов на автомобильных дорогах;

составление проекта организации строительства земляного полотна и дорожных одежд.

Ждут своего решения либо дальнейшего совершенствования в свете перехода на использование строгих математических методов оптимизации и другие задачи проектирования автомобильных дорог - такие, как пространственное трассирование автомобильных дорог, обоснование полосы варьирования трассы, проектирование специальных инженерных сооружений на автомобильных дорогах и т.д.

Широкое использование при проектировании математических методов оптимизации проектных решений, дальнейшее совершенствование их и разработка новых оптимизационных алгоритмов и программ составляют громадный резерв снижения материалоемкости и строительной стоимости автомобильных дорог и повышения эффективности инвестиций.

Моделирование предполагает построение и изучение действующих моделей (натурных, лабораторных и математических), обладающих свойствами элементов и характером их взаимодействия, подобным реальным объектам (системам). С точки зрения теории познания, под моделью понимают некоторую систему объектов, находящихся в определенных отношениях к оригиналу, изучение которой позволяет с минимальными затратами средств и времени получать новую информацию о реальной системе.

Многодельные виды моделирования такие, как натурное и лабораторное, не получили широкого распространения при проектировании автомобильных дорог, прежде всего, в связи с краткостью цикла самого проектирования.

С появлением компьютерной техники и внедрением ее в область исследований и проектирования широкое распространение получил новый, чрезвычайно эффективный метод познания - математическое моделирование.

В основе метода математического моделирования лежит идея использования хорошо известных математических уравнений для исследования явлений слабо изученных. Физическая природа процессов, развивающихся в натуре и на модели, при этом различна, однако сами процессы развиваются по одним и тем же законам.

Метод математического моделирования во многом является универсальным. Никогда еще наука не получала в свои руки столь могучего аппарата познания. Достоинствами математического моделирования являются: быстрота подготовки математической модели для выполнения тех или иных исследований; быстрота проведения цикла экспериментальных работ; возможность автоматизированной обработки результатов измерений с получением их в виде, удобном для экспериментатора; дешевизна эксперимента при минимальных материальных и трудовых затратах; получение результатов измерений в реальных масштабах пространства и времени изучаемой реальной системы.

Все особенности метода математического моделирования обеспечили широкое его внедрение не только в область научных исследований, но и в область проектирования автомобильных дорог. В математических моделях, используемых при автоматизированном проектировании автомобильных дорог, нашли применение:

аналитическая геометрия на плоскости и в пространстве. Методы аналитической геометрии широко применяют при геометрическом моделировании автомобильных дорог, транспортных развязок, водопропускных сооружений, рельефа, гидрогеологического и геологического строения местности и т.д.;

элементы теории погрешностей;

методы интерполирования функций, используемые во многих математических моделях для аппроксимации аналоговой информации (например, для аналитического представления эскизных вариантов трассы автомобильных дорог, для аппроксимации гидрометрических кривых при моделировании мостовых переходов и решении других проектных задач;

методы линейной алгебры и линейного программирования;

численные методы решения алгебраических и трансцендентных уравнений;

численные методы интегрирования дифференциальных уравнений.

В настоящее время при автоматизированном проектировании автомобильных дорог и сооружений на них с использованием методов математического моделирования решают главным образом следующие задачи:

моделирование рельефа, гидрогеологического и геологического строения местности; геометрическое моделирование элементов автомобильных дорог и развязок движения в разных уровнях;

проектирование земляного полотна;

расчет стока ливневых вод с малых водосборов;

расчет стока талых вод с малых водосборов;

расчет отверстий малых водопропускных сооружений с учетом аккумуляции; проектирование мостовых переходов;

оценка проектных решений (оценка зрительной пространственной плавности и ясности трассы, моделирование транспортных потоков, моделирование поездки одиночного расчетного автомобиля, построение киноперспектив, оценка степени загрязнения окружающей среды продуктами сгорания топлива, воздействия вибрации, шума от движущегося транспорта т.д.).

Широкое использование при проектировании автомобильных дорог методов математического моделирования, дальнейшее совершенствование их и разработка новых алгоритмов и программ с использованием принципов математического моделирования обеспечат дальнейшее значительное повышение транспортно-эксплуатационных качеств автомобильных дорог.