Непрерывные случайные величины.
Кроме дискретных случайных величин, возможные значения которых образуют конечную или бесконечную последовательность чисел, не заполняющих сплошь никакого интервала, часто встречаются случайные величины, возможные значения которых образуют некоторый интервал.
Примером такой случайной величины может служить отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе.
Такого рода, случайные величины не могут быть заданы с помощью закона распределения вероятностей 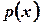 . Однако их можно задать с помощью функции распределения вероятностей F(х). Эта функция определяется точно так же, как и в случае дискретной случайной величины:
. Однако их можно задать с помощью функции распределения вероятностей F(х). Эта функция определяется точно так же, как и в случае дискретной случайной величины:
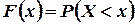
Таким образом, и здесь функция F(х) определена на всей числовой оси, и ее значение в точке х равно вероятности того, что случайная величина примет значение, меньшее, чем х.
Формула (3.4) и свойства 1° и 2° справедливы для функции распределения любой случайной величины. Доказательство проводится аналогично случаю дискретной величины.
Случайная величина 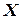 называется непрерывной, если для нее существует неотрицательная кусочно-непрерывная функция (функция называется кусочно-непрерывной на всей числовой оси, если она на любом сегменте или непрерывна, или имеет конечное число точек разрыва I рода)
называется непрерывной, если для нее существует неотрицательная кусочно-непрерывная функция (функция называется кусочно-непрерывной на всей числовой оси, если она на любом сегменте или непрерывна, или имеет конечное число точек разрыва I рода) 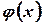 , удовлетворяющая для любых значений xравенству
, удовлетворяющая для любых значений xравенству
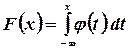 (3.5)
(3.5)
Функция 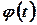 называется плотностью распределения вероятностей, или кратко, плотностью распределения. Если
называется плотностью распределения вероятностей, или кратко, плотностью распределения. Если 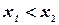 , то на основании формул (3.3) и (3.4) имеем
, то на основании формул (3.3) и (3.4) имеем
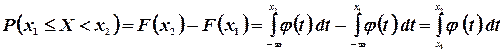 (3.6)
(3.6)
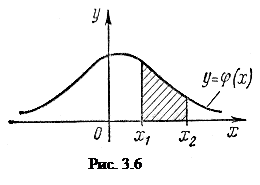
Исходя из геометрического смысла интеграла как площади, можно сказать, что вероятность выполнения неравенств 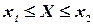 равна площади криволинейной трапеции с основанием
равна площади криволинейной трапеции с основанием 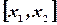 , ограниченной сверху кривой
, ограниченной сверху кривой 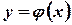 (рис. 3.6).
(рис. 3.6).
 Так как
Так как 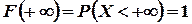 , а на основании формулы (26)
, а на основании формулы (26) 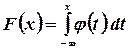 , то
, то
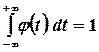 (3.7)
(3.7)
Далее, пользуясь формулой (3.5), найдем 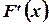 , производную от
, производную от 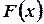 , как производную от интеграла по переменной верхней границе, считая плотность распределения
, как производную от интеграла по переменной верхней границе, считая плотность распределения 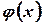 непрерывной. Правило дифференцирования интеграла с переменной верхней границей, выведенное в случае конечной нижней границы, остается справедливым и для интегралов с бесконечной нижней границей. В самом деле,
непрерывной. Правило дифференцирования интеграла с переменной верхней границей, выведенное в случае конечной нижней границы, остается справедливым и для интегралов с бесконечной нижней границей. В самом деле,
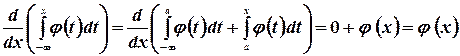
Так как интеграл 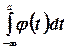 есть величина постоянная. Таким образом
есть величина постоянная. Таким образом
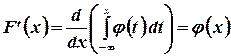 (3.8)
(3.8)
Заметим, что для непрерывной случайной величины функция распределения F(х) непрерывна в любой точке х, где функция 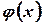 непрерывна. Это следует из того, что F(х) в этих точках дифференцируема.
непрерывна. Это следует из того, что F(х) в этих точках дифференцируема.
Далее, на основании формулы (3.6), полагая 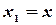 ,
, 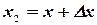 , имеем:
, имеем:
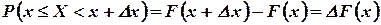
В силу непрерывности функции F(х) получим, что 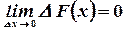 . Следовательно
. Следовательно 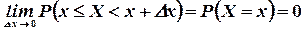 . Таким образом,
. Таким образом,
вероятность того, что непрерывная случайная величина может принять любое отдельное значение х, равна нулю.
Отсюда следует, что события, заключающиеся в выполнении каждого из неравенств: 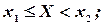
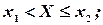
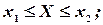
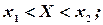 имеют одинаковую вероятность, т.е.
имеют одинаковую вероятность, т.е.
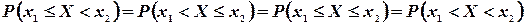
В самом деле, например,
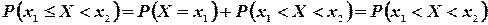
так как 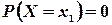 .
.
Замечание.
Как мы знаем, если событие невозможно, то вероятность его наступления равна нулю. При классическом определении вероятности, когда число исходов испытаний конечно, имеет место и обратное предложение: если вероятность события равна нулю, то событие невозможно, так как в этом случае ему не благоприятствует ни один из исходов испытания.
В случае непрерывной случайной величины число возможных ее значений бесконечно. Вероятность того, что эта величина примет какое-либо конкретное значение 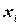 как мы видели, равна нулю. Однако отсюда не следует, что это событие невозможно, так как в результате испытания случайная величина может, в частности, принять значение
как мы видели, равна нулю. Однако отсюда не следует, что это событие невозможно, так как в результате испытания случайная величина может, в частности, принять значение 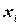 .
.
Поэтому в случае непрерывной случайной величины имеет смысл говорить о вероятности попадания случайной величины в интервал, а не о вероятности того, что она примет какое-то конкретное значение.
Так, например, при изготовлении валика нас не интересует вероятность того, что его диаметр будет равен номиналу. Для нас важна вероятность того, что диаметр валика не выходит из поля допуска.
Пример 20. Плотность распределения непрерывной случайной величины задана следующим образом:
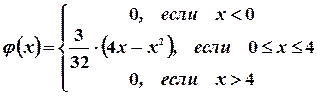
 |
График функции
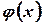 представлен па рис. 3.7.
представлен па рис. 3.7.
|
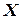 примет значение, удовлетворяющее неравенствам
примет значение, удовлетворяющее неравенствам 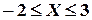 . 2) Найти функцию распределения заданной случайной величины.
. 2) Найти функцию распределения заданной случайной величины.
Решение: Используя формулу (3.6), имеем:
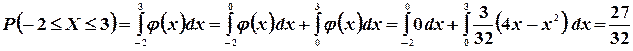
По формуле (3.6) находим функцию распределения F(x) для заданной случайной величины. Если 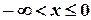 , то
, то 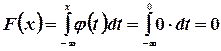 .
.
Если 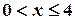 , то
, то
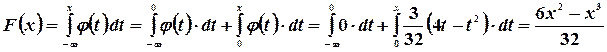 Если
Если 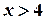 , то
, то
ч 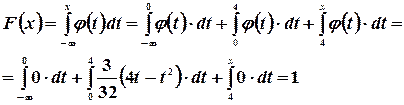
Итак,
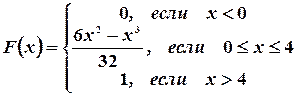
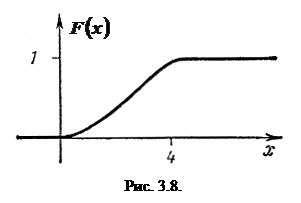
График функции F(x) изображен на рис. 3.8.
 |
Следующие три пункта посвящены часто встречающимся на практике распределениям непрерывных случайных величин — равномерному, экспоненциальному и нормальному распределениям.
5. Равномерное распределение.
Пусть сегмент 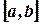 на оси Ox есть шкала некоторого прибора. Допустим, что вероятность попадания указателя в некоторый отрезок шкалы пропорциональна длине этого отрезка и не зависит от места отрезка на шкале. Отметка указателя прибора есть случайная величина
на оси Ox есть шкала некоторого прибора. Допустим, что вероятность попадания указателя в некоторый отрезок шкалы пропорциональна длине этого отрезка и не зависит от места отрезка на шкале. Отметка указателя прибора есть случайная величина 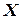 могущая принять любое значение из сегмента
могущая принять любое значение из сегмента 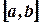 . Поэтому
. Поэтому 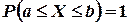 . Если, далее,
. Если, далее, 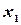 и
и 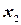
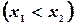 - две любые отметки на шкале, то согласно условию имеем
- две любые отметки на шкале, то согласно условию имеем 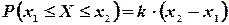 , где k - коэффициент пропорциональности, не зависящий от
, где k - коэффициент пропорциональности, не зависящий от 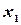 и
и 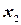 , а разность
, а разность 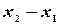 , - длина сегмента
, - длина сегмента 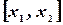 . Так как при
. Так как при 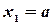 и
и 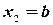 имеем
имеем 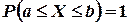 , то
, то 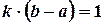 , откуда
, откуда 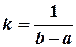 . Таким образом
. Таким образом
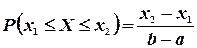 (3.9)
(3.9)
Теперь легко найти функцию F(x) распределения вероятностей случайной величины 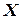 . Если
. Если 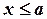 , то
, то 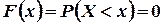 так как
так как 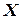 не принимает значений, меньших a. Пусть теперь
не принимает значений, меньших a. Пусть теперь 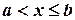 . По аксиоме сложения вероятностей
. По аксиоме сложения вероятностей 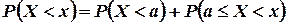 . Согласно формуле (3.9), в которой принимаем
. Согласно формуле (3.9), в которой принимаем 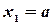 и
и 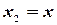 , имеем
, имеем 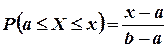 . Так как
. Так как 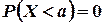 , то при
, то при 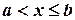 получаем
получаем 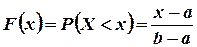 . Наконец, если
. Наконец, если 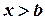 , то
, то 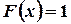 , так как значения
, так как значения 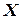 лежат на сегменте
лежат на сегменте 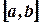 и, следовательно, не превосходят b. Итак, приходим к следующей функции распределения:
и, следовательно, не превосходят b. Итак, приходим к следующей функции распределения:
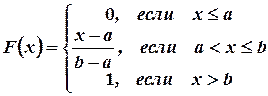 .
.
График функции F(x) представлен на рис. 3.9.
Плотность распределения вероятностей найдем по формуле (3.8). Если 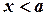 или
или 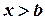 , то
, то 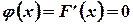 . Если
. Если 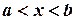 , то
, то
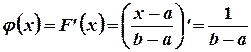 .
.
Таким образом,
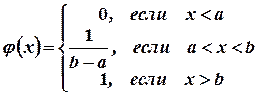 (3.10)
(3.10)
График функции 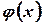 изображен на рис. 3.10. Заметим, что в точках aи b функция
изображен на рис. 3.10. Заметим, что в точках aи b функция 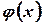 терпит разрыв.
терпит разрыв.
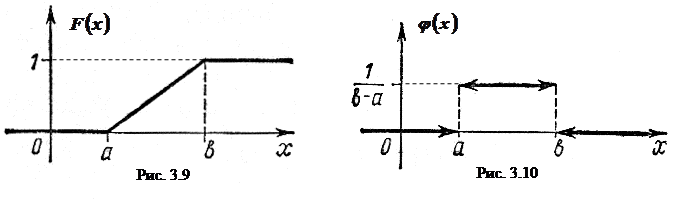
Величина, плотность распределения которой задана формулой (3.10), называется равномерно распределенной случайной величиной.
Дата добавления: 2017-02-13; просмотров: 1482;










