Этап 2. Формулировка гипотез, построение, исследование модели
Динамика изменения величины капитала определяется в нашей модели простыми процессами производства и описывается так называемыми обобщенными коэффициентами амортизации (расхода фондов) и потока инвестиций (часть конечного продукта, используемого в единицу времени для создания основных фондов). Эти коэффициенты - относительные величины (оцениваются за единицу времени). Необходимо разработать и исследовать модель динамики основных фондов. Считаем при этом допустимость определенных гипотез, определяющих систему производства.
Пусть x(t) - величина основных фондов (капитала) в момент времени t, где 0  t
t  N. Через промежуток времени Δt она будет равна x(t + Δt). Абсолютный прирост равен Δx = x(t + Δt) - x(t). Относительный прирост будет равен
N. Через промежуток времени Δt она будет равна x(t + Δt). Абсолютный прирост равен Δx = x(t + Δt) - x(t). Относительный прирост будет равен 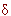 x = [x(t + Δt) - x(t)] / Δt.
x = [x(t + Δt) - x(t)] / Δt.
Примем следующие гипотезы:
1. Cоциально - экономические условия производства достаточно хорошие и способствуют росту производства, а поток инвестиций задается в виде известной функции y(t).
2. Коэффициент амортизации фондов считается неизменным и равным m, и при достаточно малом значении Δt, изменение основных фондов прямо пропорционально текущей величине капитала, т.е.
dx = y(t) - mx(t).
Считая Δt  0 и учитывая определение производной, получим из предыдущего соотношения математическое выражение закона изменения величины капитала, т.е. математическую модель (дифференциальное уравнение) динамики капитала:
0 и учитывая определение производной, получим из предыдущего соотношения математическое выражение закона изменения величины капитала, т.е. математическую модель (дифференциальное уравнение) динамики капитала:
где х(0) - начальное значение капитала в момент времени t = 0.
Эта простейшая модель не отражает важного факта: социально-экономические ресурсы производства таковы, что между выделением инвестиций и их введением и использованием в выпуске новой продукции проходит время Т (лаг). Учитывая это, можно записать модель в виде
x´(t) = y(t - T) - mx(t), x(0) = х0Этой непрерывной, дифференциальной, динамической модели можно поставить в соответствие простую дискретную модель:
хi+1 = хi + yj - mхi , x0 = с, i = 0, 1, 2, …, n,где n - предельное значение момента времени при моделировании.
Дискретная модель следует из непрерывной при Δt = 1, при замене производной x´(t) на относительное приращение , что справедливо при малых значениях Δt.
Дата добавления: 2017-02-13; просмотров: 1672;










