Уравнения движения механизма

Рис. 7.1

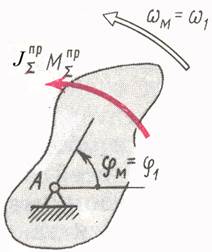Выполнив приведение сил и масс, любой механизм с одной степенью свободы (рычажный, зубчатый, кулачковый и др.), сколь бы сложным он ни был, можно заменить его динамической моде­лью (рис. 7.1). Эта модель в общем случае имеет переменный приведенный момент инерции 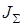и к ней приложен суммарный приведенный момент 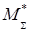. Закон движения модели такой же, как и закон движения начального звена механизма (см. уравнение 7.1).

Основой для составления уравнения движения механизма с одной степенью свободы служит теорема об изменении кинетической энергии:

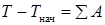(7.1)

Работу совершают все активные силы и моменты и силы трения во всех кинематических парах механизма.

Уравнение движения в энергетической форме. Запишем формулу для кинетической энергии модели, учитывая уравнение (7.1):

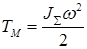. (7.2)

Так как вся нагрузка, приложенная к модели, выражается сум­марным приведенным моментом 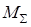, то сумма работ равна

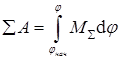(7.3)

Здесь переменная интегрирования 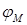заменена координатой 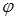начального звена, так как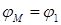

Учитывая (5.16) и подставив выражения (7.2) и (7.3) в основное уравнение (7.1), получим уравнение движения в энергетической форме:

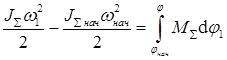(7.4)

где искомой величиной является угловая скорость 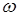начального звена механизма. В общем случае верхний предел 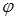интег­рирования в уравнении (7.4) считается пере­менным.

Если вся нагрузка, приложенная к меха­низму, зависит только от его положения, то и суммарный приведенный момент 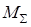есть функция только координаты 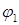. В этом слу­чае уравнение (7.4) решается непосредст­венно относительно искомой величины :

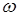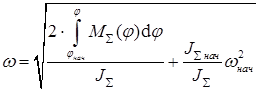(7.5)

Укажем, что интеграл под корнем имеет знак, который надо учиты­вать.

Уравнение движения в дифференциальной форме. Продифферен­цируем уравнение (7.4 по координате :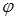

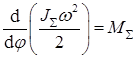
Определим производную, стоящую в левой части уравнения, помня, что в общем случае переменой величиной является не только угловая скорость 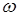, но и 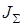. Поэтому:

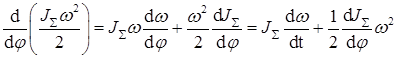
Откуда

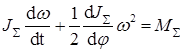(7.6)

Это и есть уравнение движения в дифференциальной форме, по­скольку искомая переменная величина — угловая скорость 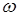на­чального звена механизма - стоит под знаком производной. При пользовании уравнением (7.6) надо помнить, что суммарный при­веденный момент 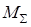, а также производная 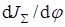суть величины алгебраические и подставляются со своими знаками.

В том случае, когда исследуется механизм, имеющий 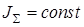(например, зубчатый механизм с круглыми колесами), уравнение его движения упрощается и приобретает такой вид:

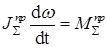(7.7)

Уравнение движения в дифференциальной форме (7.6) может быть получено также и из уравнений Лагранжа II рода [2], [4].

Для определения углового ускорения 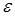начального звена используем уравнение (7.6), решим его относительно :

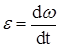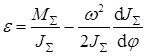(7.8)

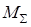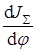Величины и подставляются в уравнение (7.8) со своими знаками. Если угловое ускорение 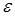получится со знаком, проти­воположным знаку угловой скорости 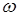, то это значит, что началь­ное звено механизма движется замедленно.

Производная 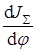подсчитывается или численным дифферен­цированием на ЭВМ, или графическим дифференцированием (см. § 4.2). Другой значительно более точный (но и более трудоемкий) способ определения производной 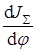можно найти в литературе

(см.: Минут С. Б. Об определении производной приведенного мо­мента инерции массы звеньев механизма// Науч. тр. МВТУ им. Н. Э. Баумана, 1970; Зиновьев В. А., Бессонов А. П. Основы динами­ки машинных агрегатов. М., 1964).