Этапы проектирования механизмов.
Проектирование плоских рычажных механизмов.
Плоские рычажные механизмы, звенья которых образуют вращательные или поступательные кинематические пары, получили широкое распространение в современном машино и приборостроении. К достоинствам механизмов относятся высокая технологичность изготовления, возможность выполнения шарнирных соединений на подшипниках качения и небольшой износ соприкасающихся поверхностей, долговечность и надежность в работе. Кроме того, для механизмов, образованных при помощи звеньев, входящих в низшие пары (в отличие от кулачковых механизмов), не требуется пружин и других устройств, обеспечивающих постоянное замыкание кинематических пар. Подавляющее большинство шарнирно-рычажных механизмов преобразует равномерное движение ведущего звена в неравномерное движение ведомого и относится к механизмам с нелинейной функцией положения ведомого звена.
Решение многих задач синтеза и анализа рычажных механизмов связано с большим объемом вычислительных операций. Поэтому автоматизация проектирования является одной из важнейших задач и фактором, определяющим технический уровень, качество и эффективность новой техники. Можно с полным основанием утверждать, что автоматизация проектирования в ближайшие годы станет одной из основных областей применения ЭВМ.
Этапы проектирования механизмов.
Проектирование механизмов представляет собой сложную комплексную проблему, решение которой разбивается на несколько этапов. Первым этапом проектирования является выбор кинематической схемы механизма, которая бы обеспечивала требуемый вид и закон движения. Ко второму этапу относится разработка конструкторских форм механизма, обеспечивающих его прочность и долговечность. Третьим этапом проектирования является разработка технологических и технико-экономических показателей проектируемого механизма.
В теории механизмов в основном рассматриваются и решаются задачи первого этапа проектирования, с помощью которых разрабатываются кинематические схемы механизмов, воспроизводящих требуемый закон движения. Проектирование механизма начинается с выбора структурной схемы. Ее выбирают из справочных материалов или разрабатывают на основе анализа видов движения, которые должны быть реализованы. Этот этап проектирования называется структурным синтезом. Разработчик должен, хотя бы в первом приближении, оценить кинематические, силовые, точностные и другие характеристики механизма, что заранее сделать трудно, а часто невозможно.
Если имеется несколько структурных схем различных механизмов, пригодных для реализации требуемых параметров, то из них следует выбрать наиболее оптимальную. На практике выбор структурной схемы производится чаще всего на основе предшествующего опыта, знаний или интуиции проектировщика. При огромном разнообразии схем одних только рычажных механизмов [1-9] такой эвристический подход к их выбору оправдан. Однако далеко не всегда проектировщик выбирает удачную структурную схему, о чем свидетельствуют конструкции многих существующих механизмов, применяемых в машинах и приборах.  Вопрос о рациональном выборе структуры проектируемого механизма сравнительно сложен [9, 12, 14, 15] , поскольку он трудно поддается формализации и недостаточно освещен в литературе по теории механизмов.
Вопрос о рациональном выборе структуры проектируемого механизма сравнительно сложен [9, 12, 14, 15] , поскольку он трудно поддается формализации и недостаточно освещен в литературе по теории механизмов.
После выбора структурной схемы механизма определяют геометрические размеры звеньев. При этом учитываются, в основном, геометрические функции, которые должен реализовать механизм. Этот этап проектирования называют этапом геометрического синтеза механизма, в режиме которого определяют относительные размеры звеньев, то есть отношение геометрических размеров звеньев к размеру одного из них. Относительные геометрические размеры звеньев называются геометрическими параметрами механизма.
Структурный и геометрический синтез позволяют получить кинематическую схему механизма, отвечающую требованиям, предъявляемым к проектируемому механизму. Геометрические функции, которые должен реализовать проектируемый механизм, воспроизводятся им с определенной точностью. Она определяется условиями работы механизма, обусловленными технологическим процессом. На основании анализа спроектированного механизма по степени точности воспроизведения заданной функции решают, пригоден ли полученный механизм или необходимо провести корректировку предыдущих этапов проектирования с изменением исходных данных. Если и повторные просчеты не дают удовлетворительных результатов, то необходимо перейти к другой структурной схеме механизма и выполнить для нее соответствующие расчеты. Этот этап проектирования называют этапом точностного проектирования.
Таким образом, задача проектирования механизма является сложной, многопараметрической, причем число исходных параметров механизма, как правило, больше числа исходных данных, поэтому частью параметров приходится варьировать.
По принципу использования рычажные механизмы делятся на следующие группы.
1. Передаточные механизмы, реализующие заданную функциональную зависимость между положениями входного и выходного звеньев механизма или между их перемещениями.
2. Направляющие механизмы, в которых точна на звене, совершающем сложное движение, перемещается при движении механизма по заданной траектории.
Решение указанных задач синтеза рычажных механизмов с низшими парами может вестись как графически, так и аналитическими методами. Выбор метода в значительной мере зависит от тех условий, которые поставлены при проектировании (в частности, точность). Графические методы нагляднее и проще с точки зрения их усвоения, но недостаточно точны. В последние годы учеными широко развиты аналитические методы синтеза механизмов с низшими парами.
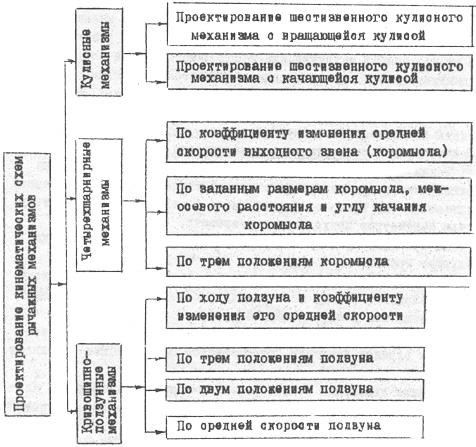 |
Схемы возможных вариантов проектирования наиболее распростанённых механизмов представлена на рис. 4.1.
Рис. 4.1. Схемы возможных вариантов проектирования механизмов
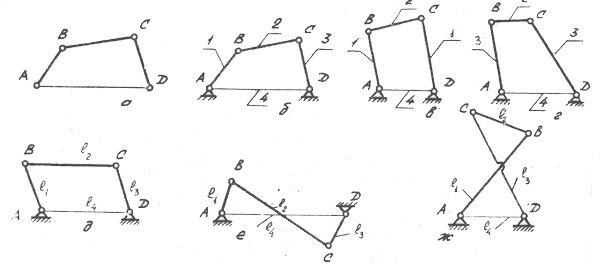
В начальной стадии проектирования машинного агрегата при выборе кинематической схемы для осуществления заданного движения, характеризуемого переменными скоростями движения рабочего органа за цикл, разработчик обращает внимание на четырехзвенные механизмы, образованные на основе четырехзвенной шарнирной кинематической цепи (рис. 4.2) или четырехзвенной цепи с тремя вращательными и одной поступательной парами (рис. 4.3).Если поставленную задачу нельзя решить с помощью четырехзвенного механизма, разработчик усложняет кинематическую схему, применяя шестизвенные или более сложные механизмы, образованные присоединением к одному из звеньев двухповодковой группы [1, 2, 4, 6]. Подробные сведения о
 |
кинематических и конструктивных модификациях приведенных механизмов можно найти в работах [1-4, 7].
Рис. 4.2. Основные виды элементарных плоских четырехзвенных механизмов: а - четырехзвенная шарнирная кинематическая цепь; б - кривошипно-коромысловый механизм; в -двухкривошипный механизм; г - двухкоромысловый механизм; д -механизм параллелограмма (l1=l3, l2=l4); е -то же, антипараллелограмма с противоположным направлением вращения кривошипов (l1 < l4); ж - то же, антипараллелограмма с одинаковым направлением вращения кривошипов (l1 > l4);
1 -кривошип; 2- шатун; 3 - коромысло; 4 -стойка
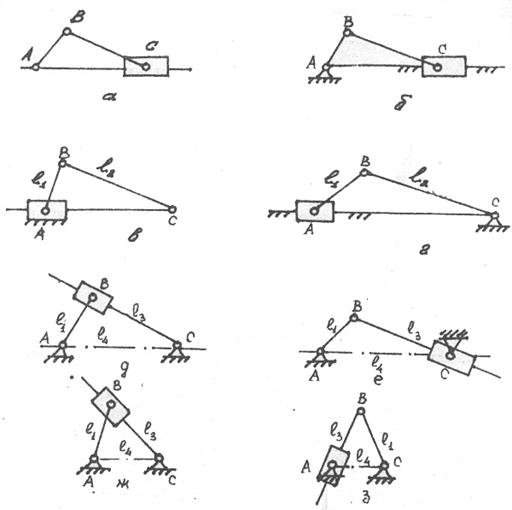
Геометрический синтез механизма заключается в определении постоянных параметров его кинематической схемы, исходя из условий задачи синтеза. Эти условия могут быть разнообразными по содержанию, но аналитически они представляют собой условия связей, накладываемых на параметры механизма, и имеют форму уравнений или неравенств. В ряде случаев условие синтеза формулируется в виде требования минимизации функции параметров механизма, принимающей неотрицательные значения.
 |
Кроме параметров механизма в условиях синтеза фигурируют обычно и задаваемые величины или функции (например, заданная для воспроизведения функция перемещения механизма, заданный угол размаха выходного звена, заданный допустимый угол давления).
Рис.4.3. Центральные четырехзвенные механизмы с тремя вращательными и одной поступательной парами: а исходная аксиальная кинематическая цепь; б - кривошипно-ползунный механизм; в - кривошипно-шатунный (l1 < l2); г - коромыслово-ползунный (l1 < l2); д, е - кривошипно-кулисный с качающейся кулисой (l1 < l4); ж, з - кривошипно-кулисный с вращающейся кулисой (l4 < l1);
Условие существования кривошипа в плоских четырехзвенных механизмах
Важной кинематической характеристикой при синтезе механизма является проворачиваемость его звеньев (наличие в нем одного или двух кривошипов), которая зависит от соотношения длин звеньев [1]. Сперва рассмотрим плоский шарнирный четырехзвенник ABCD (рис. 4.4, а) с длинами звеньев a, b, c и d. Для того чтобы звено AB могло стать кривошипом, оно должно при вращении последовательно пройти через крайние левое ( AB1) и правое ( AB3) положения.
Предполагая, что a - длина самого короткого звена, d - самого длинного, и, используя известное соотношение между длинами сторон треугольника (длина стороны треугольника меньше суммы двух других его сторон), запишем следующие неравенства:
из DB1C1D
d + a < b + c (4.1)
из DB3C3D
d - a < b + c (4.2)
Независимо от соотношения длин b и c неравенство (4.1) всегда обеспечит выполнение неравенства (4.2).
Если же самым длинным звеном является звено BC или CD (b > c > d) или (c > b > d), то неравенство только усиливается.
Позиции AB2 и AB4 характеризуют крайние положения коромысла CD. Звено BC согласно рисунку 4.4, а не делает полного оборота относительно стойки AD и потому является шатуном.
Неравенство (4.1) позволяет дать общую формулировку условия проворачиваемости звена плоского шарнирного четырехзвенника, а именно - самое короткое звено шарнирного четырехзвенника может быть кривошипом, если сумма длин самого короткого и самого длинного звеньев меньше суммы длин остальных звеньев. Это положение носит название п р а в и л а Г р а с г о ф а.
Применяя это правило, шарнирные четырехзвенники разбивают на три группы:
механизм будет кривошипно-коромысловым (рис. 4.4), если, а за стойку принято звено, расположенное рядом с самым коротким;
механизм будет двухкривошипным, если сумма длин самого короткого и самого длинного звеньев меньше суммы длин остальных звеньев и за стойку принято самое короткое его звено; это следует из того, что если кривошип при выполнении правила Грасгофа делает полный оборот относительно стойки и шатуна, то и эти звенья совершают полный оборот относительно кривошипа;
|
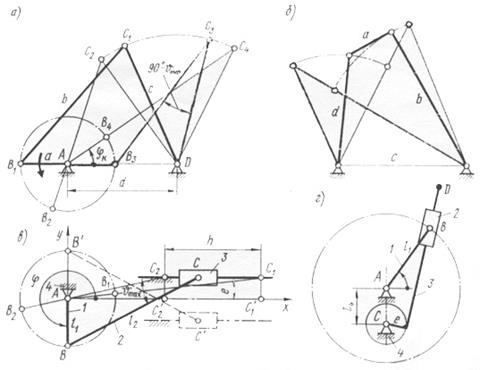 |
механизм будет двухкоромысловым, если размеры его звеньев не удовлетворяют правилу, а также в том случае, когда сумма длин самого короткого и самого длинного звеньев меньше суммы длин остальных звеньев, но самое короткое его звено является шатуном (рис. 4.4, б), и, следовательно, возможность быть ему кривошипом отпадает, потому что оно не является звеном, расположенным рядом со стойкой.
В предельном случае, когда неравенство (4.1) превращается в равенство, все звенья механизма в одном из крайних положений располагаются по одной прямой. В результате получится неопределенность движения выходного звена (оно сможет двигаться либо в одном, либо в другом направлении).
Во всеосном кривошипно-ползунном механизме (рис. 4.4, в) звено l будет кривошипом, если при вращении пройдет положения j = 90 и 270°, что возможно при выполнении условия
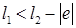 (4.3)
(4.3)
где e - внеосность (или дезаксиал). Штриховой линией изображена схема, когда e < 0. Если l1 > l2 - | e | , звено l будет коромыслом, и такой механизм правильнее называть коромыслово-ползунным.
В кулисном механизме (рис. 4.4, г) звено l всегда может быть кривошипом, звено CD (кулиса) будет кривошипом, если при вращении пройдет положение j = 270°, что возможно при выполнении условия
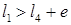 (4.4)
(4.4)
где e - внеосность кулисы; в этом случае имеем механизм с вращающейся кулисой. Если l1 < l4 + e , то кулиса CD будет коромыслом (механизм с качающейся кулисой). Наиболее распространены схемы кулисных механизмов, в которых внеосность e = 0.
Дата добавления: 2017-02-13; просмотров: 5163;










