Построение функции Грина для пространства изображений

Тогда функция Грина примет вид:

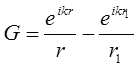(24.16)

Очевидно, при 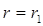G=0 на всей плоскости выходного зрачка Σ-Σ'. gradG при этом равен:

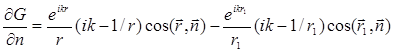
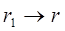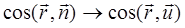При и , тогда

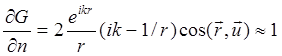(24.17)

Сделав естественное для оптического диапазона предположение (дифракция Фраунгофера)

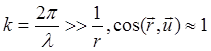(24.18)

получим:

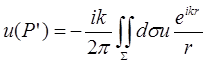(24.19)

Из (24.19) следует, что каждый элемент излучающей поверхности дает свой вклад в возмущение в точке Р’, представляющее собой суперпозицию сферических волн. Припишем точке Р’ координаты (x,y), а элементу dσ ― (u,v). Идеальная оптическая система давала бы сферический волновой фронт с центром в точке P’: 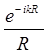. Но реальная поверхность будет отличаться от сферы на некоторую (малую) величину 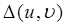. Поэтому запишем:

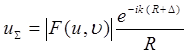, (24.20)

вводя 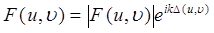― комплексную амплитуду возмущения на выходном зрачке. Подставляя (24.20) в (24.19), получим:

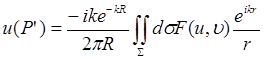(24.21)

Здесь 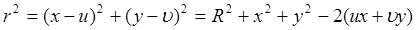. В силу параксиальности (рассматриваем возмущение в небольшой области вокруг луча R) можно разложить r в показателе степени в ряд:

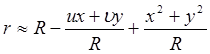(24.22)

пренебрегая членами более высокого порядка, а 1/r вынести за знак интеграла. Тогда формула (24.21) примет вид:

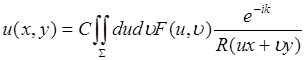(24.23)

В (24.23) введена постоянная С, обозначающая все члены, не зависящие от u и v.

Преобразуем (24.23) к более удобному виду с помощью обозначений:

; ; ;

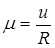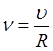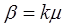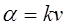
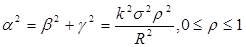(24.24)

Кроме того, определим F(β,γ) так, что F(β,γ) = 0 при .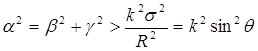

Тогда (24.23) представляет собой не что иное, как двумерное преобразование Фурье от возмущения в пределах выходного зрачка (с точностью до постоянной):

u(x,y)=A 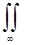dβdγ F(β,γ)exp(-i(βx - γy)) (24.25)

Выражение (24.25) имеет различные представления для случаев когерентного и некогерентного освещения F(β,γ) выходного зрачка.

Рассмотрим сначала некогерентный случай: линейно суммируется функция 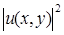, которая и представляет собой функцию Грина оптической системы:

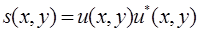(24.26)

Нормализованная передаточная функция для этого случая равна:

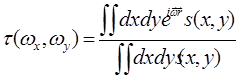(24.27)

Поскольку s(x,y) представляет собой произведение двух функций, можно (24.27) переписать, воспользовавшись теоремой свертки, в виде:

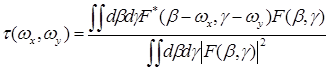(24.28)

Выражение (24.28) имеет важное значение. Именно, оно:

1. Непосредственно показывает, как деформация волнового фронта влияет на пространственно-частотную характеристику. Поэтому можно определить ЧКХ непосредственно по информации только в пределах выходного зрачка.

2. Смещение частоты обеспечивает некоторое сглаживание τ(ω), поэтому часто удобнее работать с τ(ω), а не с s(x,y).

3. (24.28) ― следствие двух вообще различных преобразований Фурье. Первое: u(x,y) ↔ F(β,γ) ― при использовании принципа Гюйгенса построение можно рассматривать как двумерное преобразование Фурье распределения амплитуды в пределах выходного зрачка. Второе: формирование оптического изображения есть фильтрация пространственных частот.

Используя формулы (24.25) ― (24.28), можно с успехом строить изображение в оптических системах, освещаемых некогерентным светом (дифракция на щели, дифракция на круглом отверстии, построение изображений линейного источника через систему щелей и т.д.). При этом весьма изящно описываются малые аберрации оптических систем и даются рецепты улучшения качества изображения с помощью выбора передаточных функций.

Наш же интерес главным образом связан со случаем когерентного освещения, поскольку возможности пространственной фильтрации здесь существенно больше. В самом деле, если квадрат электрического вектора складывается линейно от точки к точке, то оптическая система всегда ведет себя как фильтр нижних частот. Если же мы имеем возможность воздействовать как на амплитудные, так и ― особенно! ― на фазовое распределение точечного изображения, то такой фильтр является, вообще говоря, широкополосным и может быть сделан столь же многообразным, как электрические фильтры в радиотехнике. Это возможно только при когерентном освещении в плоскости объекта, реально осуществимом с помощью лазерных источников. Ввиду особой важности случая когерентного освещения мы уделим ему особое внимание ниже.